深入浅出Word2Vec原理解析

最新推荐文章于 2025-10-27 22:54:06 发布

原创

最新推荐文章于 2025-10-27 22:54:06 发布 · 1.9k 阅读

10 ·

CC 4.0 BY-SA版权

本文概览：
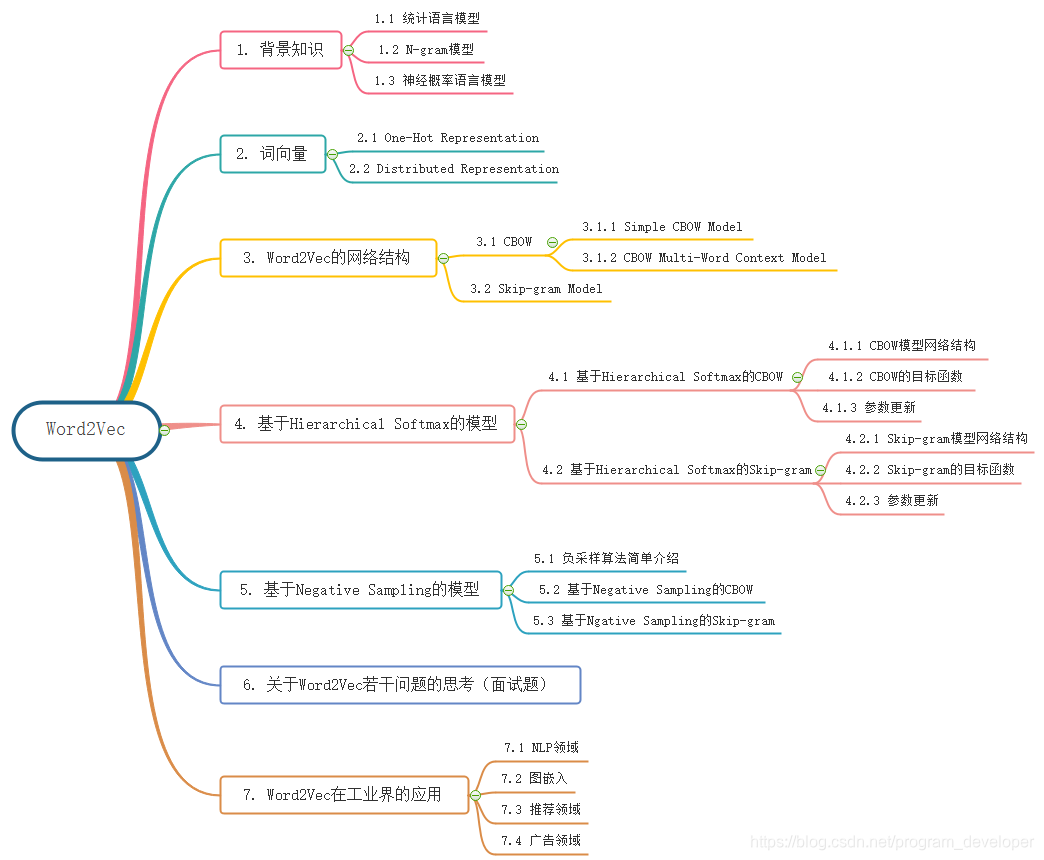
在这里插入图片描述

1. 背景知识

Word2Vec是语言模型中的一种，它是从大量文本预料中以无监督方式学习语义知识的模型，被广泛地应用于自然语言处理中。

Word2Vec是用来生成词向量的工具，而词向量与语言模型有着密切的关系。因此，我们先来了解一些语言模型方面的知识。

1.1 统计语言模型

统计语言模型是用来计算一个句子的概率的概率模型，它通常基于一个语料库来构建。那什么叫做一个句子的概率呢？假设 $W = (w_{1}, w_{2}, ..., w_{T})$ 表示由 $T$ 个词 $w_{1},w_{2},...,w_{T}$ 按顺序构成的一个句子，则 $w_{1},w_{2},...,w_{T}$ 的联合概率为：
$p(W) = p(w_{1},w_{2},...,w_{T})$
$p (W)$ 被称为语言模型，即用来计算这个句子概率的模型。利用Bayes公式，上式可以被链式地分解为：
$p(w_{1})p(w_{2}|w_{1})p(w_{3}|w_{1},w_{2})...p(w_{T}|w_{1},w_{2},...,w_{T-1}) \tag{1}$
其中的条件概率 $p(w_{1}),p(w_{2}|w_{1}),...,p(w_{T}|w_{1},w_{2},...,w_{T-1})$ 就是语言模型的参数，若这些参数已经全部算得，那么给定一个句子 $W$ ，就可以很快地计算出相应地概率 $p (W)$ 了。

看起来好像很简单，是吧？但是，具体实现起来还是有点麻烦。例如，先来看看模型参数的个数。刚才是考虑一个给定的长度为T的句子，就需要计算T个参数。不防假设语料库对应词典 $D$ 的大小（即词汇量）为 $N$ ，那么，如果考虑长度为 $T$ 的任意句子，理论上就有 $N^{T}$ 种可能，而每种可能都要计算 $T$ 个参数，总共就需要计算 $TN^{T}$ 个参数。当然，这里只是简单估算，并没有考虑重复参数，但这个量级还是有点吓人。此外，这些概率计算好后，还得保存下来，因此，存储这些信息也需要很大的内存开销。

此外，这些参数如何计算呢？常见的方法有n-gram模型、决策树、最大熵模型、最大熵马尔可夫模型、条件随机场、神经网络等方法。本文只讨论n-gram模型和神经网络两种方法。

1.2 N-gram模型

考虑 $p(w_{k}|w_{1},..., w_{k-1})$ 的近似计算。利用Bayes公式，有：
$p(w_{k}|w_{1},...,w_{k-1}) = \frac{p(w_{1},...,w_{k})}{p(w_{1},...,w_{k-1})}$

根据大数定理，当语料库足够大时， $p(w_{k}|w_{1},...,w_{k-1})$ 可以近似地表示为：
$p(w_{k}|w_{1},...,w_{k-1}) \approx \frac{count(w_{1},...,w_{k})}{count(w_{1},...,w_{k-1})} \tag{2}$
其中， $count(w_{1},...,w_{k})$ 表示词串 $w_{1},...,w_{k}$ 在语料中出现的次数， $count(w_{1},...,w_{k-1})$ 表示词串 $w_{1},...,w_{k-1}$ 在语料中出现的次数。可想而知，当 $k$ 很大时， $count(w_{1},...,w_{k})$ 和 $count(w_{1},...,w_{k-1})$ 的统计将会多么的耗时。

从公式（1）可以看出：一个词出现的概率与它前面的所有词都相关。如果假定一个词出现的概率只与它前面固定数目的词相关呢？这就是n-gram模型的基本思想，它做了一个 $n - 1$ 阶的Markov假设，认为一个词出现的概率就只与它前面的 $n - 1$ 个词相关，即，
$p(w_{k}|w_{1},...,w_{k-1}) \approx p(w_{k}|w_{k-n+1},...,w_{k-1})$
于是，公式（2）就变成了
$p(w_{k}|w_{1},...,w_{k-1}) \approx \frac{count(w_{k-n+1},...,w_{k})}{count(w_{k-n+1},...,w_{k-1})} \tag{3}$

以 $n = 2$ 为例，就有
$p(w_{k}|w_{1},...,w_{k-1}) \approx \frac{count(w_{k-1},...,w_{k})}{count(w_{k-1})}$

这样简化，不仅使得单个参数的统计变得更容易（统计时需要匹配的词串更短），也使得参数的总数变少了。

那么，n-gram中的参数 $n$ 取多大比较合适呢？一般来说，n的选取需要同时考虑计算复杂度和模型效果两个因素。

表1：模型参数数量与n的关系

n	模型参数的数量
1(unigram)	$\times 10^{5}$
2(bigram)	$\times 10^{10}$
3(trigram)	$\times 10^{15}$
4(4-gram)	$16 \times 10^{20}$

在计算复杂度方面，表1给出了n-gram模型中模型参数数量随着 $n$ 的逐渐增大而变化的情况，其中假定词典大小 $N = 200000$ (汉语的词汇量大大致是这个量级)。事实上，模型参数的量级是 $N$ 的指数函数( $O(N^{n})$ )，显然 $n$ 不能取得太大，实际应用中最多是采用 $n = 3$ 的三元模型。

在模型效果方面，理论上是 $n$ 越大，效果越好。现如今，互联网的海量数据以及机器性能的提升使得计算更高阶的语言模型（如 $n > 10$ ）成为可能，但需要注意的是，当 $n$ 大到一定程度时，模型效果的提升幅度会变小。例如，当 $n$ 从 $1$ 到 $2$ ，再从 $2$ 到 $3$ 时，模型的效果上升显著，而从 $3$ 到 $4$ 时，效果的提升就不显著了（具体可以参考吴军在《数学之美》中的相关章节）。事实上，这里还涉及到一个可靠性和可区别性的问题，参数越多，可区别性越好，但同时单个参数的实例变少从而降低了可靠性，因此需要在可靠性和可区别性之间进行折中。

另外，n-gram模型中还有一个叫做平滑化的重要环节。回到公式（3），考虑两个问题：

若 $count(w_{k-n+1},..., w_{k}) = 0$ , 能否认为 $p(w_{k} | w_{1},...,w_{k-1})$ 就等于 $0$ 呢？
若 $count(w_{k-n+1},..., w_{k})$ = $count(w_{k-n+1}, ..., w_{k-1})$ ，能否认为 $p(w_{k}|w_{1},...,w_{k-1})$ 就等于 $1$ 呢？

显然不能，但这是一个无法回避的问题，哪怕你的预料库有多么大。平滑化技术就是用来处理这个问题的，这里不展开讨论。

总结起来，n-gram模型是这样一种模型，其主要工作是在语料中统计各种词串出现的次数以及平滑化处理。概率值计算好之后就存储起来，下次需要计算一个句子的概率时，只需找到相关的概率参数，将它们连乘起来就好了。

然而，在机器学习领域有一种通用的解决问题的方法：对所考虑的问题建模后先为其构造一个目标函数，然后对这个目标函数进行优化，从而求得一组最优的参数，最后利用这组最优参数对应的模型来进行预测。

对于统计语言模型而言，利用最大似然，可把目标函数设为：
$\prod_{w \in C}^{} p(w|Context(w))$
其中， $C$ 表示语料(Corpus)， $C o n t e x t (w)$ 表示词 $w$ 的上下文，即 $w$ 周边的词的集合。当 $C o n t e x t (w)$ 为空时，就取 $p (w ∣ C o n t e x t (w)) = p (w)$ 。特别地，对于前面介绍的n-gram模型，就有 $Context(w_{i} = w_{i-n+1},...,w_{i-1})$ 。

当然，实际应用中常采用最大对数似然，即把目标函数设为
$\sum_{w \in C}^{}{log p(w|Context(w))} \tag{4}$
然后对这个函数进行最大化。

从公式（4）可见，概率 $p (w ∣ C o n t e x t (w))$ 已被视为关于 $w$ 和 $C o n t e x t (w)$ 的函数，即：
$\theta)$
其中 $θ\theta$ 为待定参数集。这样一来，一旦对公式（4）进行优化得到最优参数集 $θ∗\theta^{ *}$ 后， $F$ 也就唯一被确定了，以后任何概率 $p (w ∣ C o n t e x t (w))$ 就可以通过函数 $\theta^{ *})$ 来计算了。与n-gram相比，这种方法不需要事先计算并保存所有的概率值，而是通过直接计算来获取，且通选取合适的模型可使得 $θ\theta$ 中参数的个数远小于n-gram中模型参数的个数。

很显然，对于这样一种方法，最关键的地方就在于函数 $F$ 的构建了。下一小节将介绍一种通过神经网络来构造 $F$ 的方法。之所以特意介绍这个方法，是因为它可以视为Word2Vec中算法框架的前身或者说基础。

1.3 神经概率语言模型

本小节介绍 Bengio 等人于2003年在论文《A Neural Probabilistic Language Model》中提出的一种神经概率语言模型。该论文首次提出用神经网络来解决语言模型的问题，虽然在当时并没有得到太多的重视，却为后来深度学习在解决语言模型问题甚至很多别的nlp问题时奠定了坚实的基础，后人站在Yoshua Bengio的肩膀上，做出了更多的成就。包括Word2Vec的作者Tomas Mikolov在NNLM的基础上提出了RNNLM和后来的Word2Vec。文中也较早地提出将word表示一个低秩的向量，而不是One-Hot。word embedding作为一个language model的副产品，在后面的研究中起到了关键作用，为研究者提供了更加宽广的思路。值得注意的是Word2Vec的概念也是在该论文中提出的。

什么是词向量呢？简单来说就是，对词典 $D$ 中的任意词 $w$ ，指定一个固定长度的实值向量 $\in \Re ^{m}$ , $v (w)$ 就称为 $w$ 的词向量， $m$ 为词向量的长度。关于词向量的进一步理解将放到下一节来讲解。

既然是神经概率语言模型，其中当然要用到神经网络了。下图给出了神经网络的结构示意图。模型一共三层，第一层是映射层，将 $n$ 个单词映射为对应word embeddings的拼接，其实这一层就是MLP的输入层；第二层是隐藏层，激活函数用 $t a n h$ ；第三层是输出层，因为是语言模型，需要根据前 $n$ 个单词预测下一个单词，所以是一个多分类器，用 $S o f t m a x$ 。整个模型最大的计算量集中在最后一层上，因为一般来说词汇表都很大，需要计算每个单词的条件概率，是整个模型的计算瓶颈。

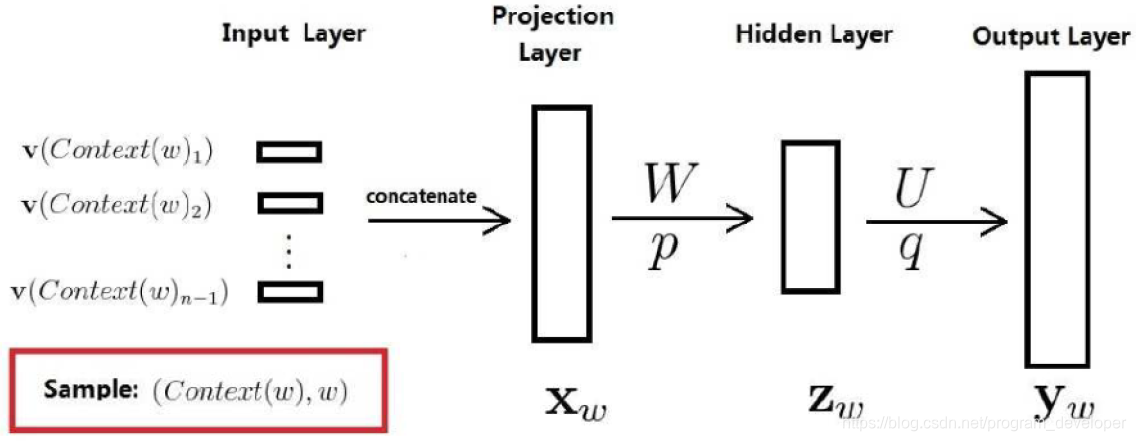
在这里插入图片描述

经过上面步骤的计算得到的 $y_{w} = (y_{w,1}, y_{w,2},...,y_{w,N})^{T}$ 只是一个长度为 $N$ 的向量，其分量不能表示概率。如果想要 $y_{w}$ 的分量 $y_{w,i}$ 表示当上下文为 $C o n t e x t (w)$ 时下一个词恰为词点 $D$ 中第 $i$ 个词的概率，则还需要做一个Softmax归一化，归一化后，$ p(w|Context(w))$ 就可以表示为：
$\frac{e^{y_{w,i_{w}}}}{ \sum_{i=1}^{N}{e^{y_{w,i}}}} \tag{5}$
其中 $i_{w}$ 表示词 $w$ 在词典 $D$ 中的索引。