SharpICTCLAS分词系统简介(4)NShortPath-1

原文地址：http://www.cnblogs.com/zhenyulu/articles/669795.html

N-最短路径中文词语粗分是分词过程中非常重要的一步，而原有ICTCLAS中该部分代码也是我认为最难读懂的部分，到现在还有一些方法没有弄明白，因此我几乎重写了NShortPath类。要想说明N-最短路径代码是如何工作的并不容易，所以分成两步分，本部分先说说SharpICTCLAS中1-最短路径是如何实现的，在下一篇文章中再引申到N-最短路径。

1、数据表示

这里我们求最短路的例子使用如下的有向图，每条边的权重已经在图中标注出来了。

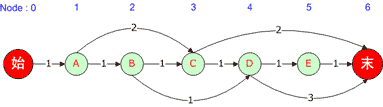
（图一）

根据上篇文章内容，该图该可以等价于如下的二维表格表示：

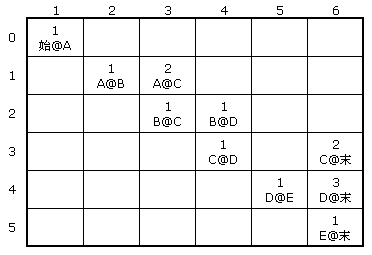
（图二）

而对应于该表格的是一个ColumnFirstDynamicArray，共有10个结点，每个结点的取值如下表所示：

  Copy Code

该示例对应的ColumnFirstDynamicArray

row:0,  col:1,  eWeight:1,  nPOS:0,  sWord: 始@A 
row:1,  col:2,  eWeight:1,  nPOS:0,  sWord: A@B 
row:1,  col:3,  eWeight:2,  nPOS:0,  sWord: A@C 
row:2,  col:3,  eWeight:1,  nPOS:0,  sWord: B@C 
row:2,  col:4,  eWeight:1,  nPOS:0,  sWord: B@D 
row:3,  col:4,  eWeight:1,  nPOS:0,  sWord: C@D 
row:4,  col:5,  eWeight:1,  nPOS:0,  sWord: D@E 
row:3,  col:6,  eWeight:2,  nPOS:0,  sWord: C@末 
row:4,  col:6,  eWeight:3,  nPOS:0,  sWord: D@末 
row:5,  col:6,  eWeight:1,  nPOS:0,  sWord: E@末

2、计算出每个结点上可达最短路的PreNode

在求解N-最短路径之前，先看看如何求最短PreNode。如下图所示：

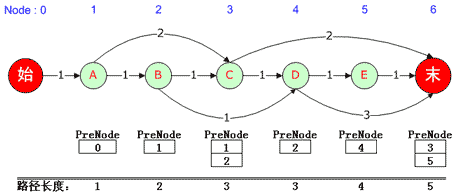
（图三）

首先计算出到达每个结点的最短路径，并将该结点的父结点压入该结点所对应的队列。例如3号“C”结点，到达该结点的最短路径长度为3，它的Parent结点可以是1号“A”结点，也可以是2号“B”结点，因此在队列中存储了两个PreNode结点。

而在实际计算时，如何知道到达3号“C”结点的路径有几条呢？其实我们首先计算所有到达3号“C”结点的路径长度，并按照路径长度从小到大的顺序排列（所有这些都是靠CQueue这个类完成的），然后从队列中依次向后取值，取出所有最短路径对应的PreNode。

计算到当前结点（nCurNode）可能的边，并根据总路径长度由小到大压入队列的代码如下（经过简化）：

  Copy Code

EnQueueCurNodeEdges方法

//==================================================================== 
// 将所有到当前结点（nCurNode）可能的边根据eWeight排序并压入队列 
//==================================================================== 
private  void EnQueueCurNodeEdges( ref CQueue queWork,  int nCurNode) 
{ 
    int nPreNode; 
    double eWeight; 
   ChainItem<ChainContent> pEdgeList; 

   queWork.Clear(); 
   pEdgeList = m_apCost.GetFirstElementOfCol(nCurNode); 

    // 获取所有到当前结点的边 
    while (pEdgeList !=  null && pEdgeList.col == nCurNode) 
   { 
      nPreNode = pEdgeList.row;   //  很特别的命令，利用了row与col的关系  
      eWeight = pEdgeList.Content.eWeight; 

       // 第一个结点，没有PreNode，直接加入队列 
       if (nPreNode == 0) 
      { 
         queWork.EnQueue( new QueueElement(nPreNode, eWeight)); 
          break; 
      } 

      queWork.EnQueue( new QueueElement(nPreNode, eWeight + m_pWeight[nPreNode - 1])); 
      pEdgeList = pEdgeList.next; 
   } 
} 

这段代码中有一行很特别的命令，就是用红颜色注释的那句“nPreNode = pEdgeList.row;”，让我琢磨了半天终于弄明白原有ICTCLAS用意的一句话。这需要参考本文图二，为了方便起见，我将它挪到了这里：

注意 3 号“C”结点在该表中处于第 3 列，所有可以到达该结点的边就是该列中的元素（目前有两个元素“A@C”与“B@C”）。而与 3 号“C”结点构成这两条边的PreNode结点恰恰是这两个元素的“行号”，分别是 1 号“A”结点与 2 号“B”结点。正是因为这种特殊的对应关系，为我们检索所有可达边提供了便捷的方法。阅读上面那段代码务必把握好这种关系。

3、求解最短路径

求出每个结点上最短路径的PreNode后就需要据此推导出完整的最短路径。原ICTCLAS代码中是靠GetPaths方法实现的，只是到现在我也没有读懂这个方法的代码究竟想干什么 ，只知道它用了若干个while，若干个if，若干个嵌套...（将ICTCLAS中的GetPaths放上来，如果谁读懂了，回头给我讲讲 ，感觉应该和我的算法差不多）。

  Copy Code

NShortPath.cpp程序中的GetPaths方法

void CNShortPath::GetPaths(unsigned  int nNode, unsigned  int nIndex,  int 
  **nResult,  bool bBest) 
{ 
  CQueue queResult; 
  unsigned  int nCurNode, nCurIndex, nParentNode, nParentIndex, nResultIndex = 0; 

   if (m_nResultCount >= MAX_SEGMENT_NUM) 
   //Only need 10 result 
     return ; 
  nResult[m_nResultCount][nResultIndex] =  - 1;  //Init the result  
  queResult.Push(nNode, nIndex); 
  nCurNode = nNode; 
  nCurIndex = nIndex; 
   bool bFirstGet; 
   while (!queResult.IsEmpty()) 
  { 
     while (nCurNode > 0) 
     // 
    { 
       //Get its parent and store them in nParentNode,nParentIndex 
       if (m_pParent[nCurNode - 1][nCurIndex].Pop(&nParentNode, &nParentIndex, 0, 
         false,  true) !=  - 1) 
      { 
        nCurNode = nParentNode; 
        nCurIndex = nParentIndex; 
      } 
       if (nCurNode > 0) 
        queResult.Push(nCurNode, nCurIndex); 
    } 
     if (nCurNode == 0) 
    { 
       //Get a path and output 
      nResult[m_nResultCount][nResultIndex++] = nCurNode;  //Get the first node 
      bFirstGet =  true; 
      nParentNode = nCurNode; 
       while (queResult.Pop(&nCurNode, &nCurIndex, 0,  false, bFirstGet) !=  - 1) 
      { 
        nResult[m_nResultCount][nResultIndex++] = nCurNode; 
        bFirstGet =  false; 
        nParentNode = nCurNode; 
      } 
      nResult[m_nResultCount][nResultIndex] =  - 1;  //Set the end 
      m_nResultCount += 1;  //The number of result add by 1 
       if (m_nResultCount >= MAX_SEGMENT_NUM) 
       //Only need 10 result 
         return ; 
      nResultIndex = 0; 
      nResult[m_nResultCount][nResultIndex] =  - 1;  //Init the result  

       if (bBest) 
       //Return the best result, ignore others 
         return ; 
    } 
    queResult.Pop(&nCurNode, &nCurIndex, 0,  false,  true);  //Read the top node 
     while (queResult.IsEmpty() ==  false && (m_pParent[nCurNode - 
      1][nCurIndex].IsSingle() || m_pParent[nCurNode - 1][nCurIndex].IsEmpty 
      ( true))) 
    { 
      queResult.Pop(&nCurNode, &nCurIndex, 0);  //Get rid of it 
      queResult.Pop(&nCurNode, &nCurIndex, 0,  false,  true);  //Read the top node 
    } 
     if (queResult.IsEmpty() ==  false && m_pParent[nCurNode - 
      1][nCurIndex].IsEmpty( true) ==  false) 
    { 
      m_pParent[nCurNode - 1][nCurIndex].Pop(&nParentNode, &nParentIndex, 0, 
         false,  false); 
      nCurNode = nParentNode; 
      nCurIndex = nParentIndex; 
       if (nCurNode > 0) 
        queResult.Push(nCurNode, nCurIndex); 
    } 
  } 
}

我重写了求解最短路径的方法，其算法表述如下：

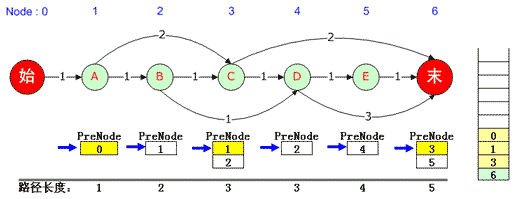
（图四）

1）首先将最后一个元素压入堆栈（本例中是6号结点），什么时候这个元素弹出堆栈，什么时候整个任务结束。

2）对于每个结点的PreNode队列，维护了一个当前指针，初始状态都指向PreNode队列中第一个元素。

3）从右向左依次取出PreNode队列中的当前元素并压入堆栈，并将队列指针重新指向队列中第一个元素。如图四：6号元素PreNode是3，3号元素PreNode是1，1号元素PreNode是0。

4）当第一个元素压入堆栈后，输出堆栈内容即为一条队列。本例中0, 1, 3, 6便是一条最短路径。

5）将堆栈中的内容依次弹出，每弹出一个元素，就将当时压栈时对应的PreNode队列指针下移一格。如果到了末尾无法下移，则继续执行第5步，如果仍然可以移动，则执行第3步。

对于本例，先将“0”弹出堆栈，该元素对应的是1号“A”结点的PreNode队列，该队列的当前指针已经无法下移，因此继续弹出堆栈中的“1” ；该元素对应3号“C”结点，因此将3号“C”结点对应的PreNode队列指针下移。由于可以移动，因此将队列中的2压入队列，2号“B”结点的PreNode是1，因此再压入1，依次类推，直到0被压入，此时又得到了一条最短路径，那就是0，1，2，3，6。如下图：

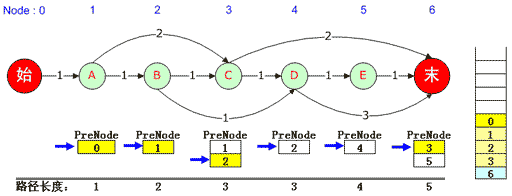
（图五）

再往下，0、1、2都被弹出堆栈，3被弹出堆栈后，由于它对应的6号元素PreNode队列记录指针仍然可以下移，因此将5压入堆栈并依次将其PreNode入栈，直到0被入栈。此时输出第3条最短路径：0, 1, 2, 4, 5, 6。入下图：

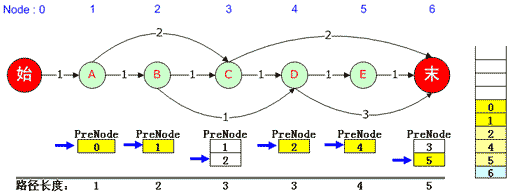
（图六）

输出完成后，紧接着又是出栈，此时已经没有任何堆栈元素对应的PreNode队列指针可以下移，于是堆栈中的最后一个元素6也被弹出堆栈，此时输出工作完全结束。我们得到了3条最短路径，分别是：

• 0, 1, 3, 6,
• 0, 1, 2, 3, 6,
• 0, 1, 2, 4, 5, 6,

让我们看看在SharpICTCLAS中，该算法是如何实现的：

  Copy Code

SharpICTCLAS中的GetPaths方法

//==================================================================== 
// 注：index ＝ 0 : 最短的路径； index = 1 ： 次短的路径 
//     依此类推。index <= this.m_nValueKind 
//==================================================================== 
public List< int[]> GetPaths( int index) 
{ 
   Stack<PathNode> stack =  new Stack<PathNode>(); 
    int curNode = m_nNode - 1, curIndex = index; 
   QueueElement element; 
   PathNode node; 
    int[] aPath; 
   List< int[]> result =  new List< int[]>(); 

   element = m_pParent[curNode - 1][curIndex].GetFirst(); 
    while (element !=  null) 
   { 
       // ---------- 通过压栈得到路径 ----------- 
      stack.Push( new PathNode(curNode, curIndex)); 
      stack.Push( new PathNode(element.nParent, element.nIndex)); 
      curNode = element.nParent; 

       while (curNode != 0) 
      { 
         element = m_pParent[element.nParent - 1][element.nIndex].GetFirst(); 
         stack.Push( new PathNode(element.nParent, element.nIndex)); 
         curNode = element.nParent; 
      } 

       // -------------- 输出路径 -------------- 
      PathNode[] nArray = stack.ToArray();             
      aPath =  new  int[nArray.Length]; 
       
       for( int i=0; i<aPath.Length; i++) 
         aPath[i] = nArray[i].nParent; 

      result.Add(aPath); 

       // -------------- 出栈以检查是否还有其它路径 -------------- 
       do 
      { 
         node = stack.Pop(); 
         curNode = node.nParent; 
         curIndex = node.nIndex; 

      }  while (curNode < 1 || (stack.Count != 0 && !m_pParent[curNode - 1][curIndex].CanGetNext)); 

      element = m_pParent[curNode - 1][curIndex].GetNext(); 
   } 

    return result; 
}

注意，上面的代码是N-最短路径的，比起1-最短路径来说增加了点复杂度，但总体架构不变。这段代码将原有ICTCLAS的70多行求解路径代码缩短到了40多行。

• 小结

1）N-最短路径的求解比较复杂，本文先从求解1-最短路径着手，说明SharpICTCLAS是如何计算的，在下篇文章中将推广到N-最短路径。

2）1-最短路径并不意味着只有一条最短路径，而是路径最短的若干条路径。就如本文案例所示，1-最短路径算法最终求得了3条路径，它们的长度都是5，因此都是最短路径。