文章目录
P o s i t i v e Positive Positive 数据中的正类数
N e g a t i v e Negative Negative 数据中的反类数
分类预测结果出现四种情况
T r u e P o s i t i v e TruePositive TruePositive ---- 将正类预测为正类数, 真正例, 真阳性.
F
a
l
s
e
P
o
s
i
t
i
v
e
FalsePositive
FalsePositive ---- 将负类预测为正类数, 假正例, 假阳性
在统计学假设检验中被称为第 I 类错误. 零假设
H
0
H_0
H0 为不是正类, 结果把它判定为正类而拒绝(reject)
H
0
H_0
H0 (incorrectly reject the null hypothesis[6], 弃真[3]). 测试怀孕为阳性, 事实上没有怀孕(
H
0
H_0
H0为没有怀孕).
p.s. 在统计学中, 一般零假设是一个被普遍接受的假设, 认为其它的观测数据或者现象是偶然的、没有什么新奇的、与观测到的现象没有什么关联, 而检验人员由自己所观测到的数据或者现象提出备择假设并试图用相反的证据使零假设无效[5], [7], [8]. 如 H 0 H_0 H0 地球不是宇宙的中心. 一位业余天文爱好者坐在那里观察星星、太阳、月亮绕着地球转, 而认为 H 0 H_0 H0是无效假设, 犯了一类假阳性错误.
F
a
l
s
e
N
e
g
a
t
i
v
e
FalseNegative
FalseNegative ---- 将正类预测为负类数, 假反例,
在统计学假设检验中被称为第 II 类错误. 零假设
H
0
H_0
H0 为负类, 结果把正类的判定为负类而接受(not reject)
H
0
H_0
H0. 样本容量固定不变的情况下,想办法减少犯一类错误的概率可能会增加犯二类错误的概率, 反之亦然 [3]. 假设检验中, 固定样本容量的情况下, 一般控制一类发生的概率, 而不考虑二类发生的概率, 这种检验称为显著性检验 [3].
T r u e N e g a t i v e TrueNegative TrueNegative ---- 将负类预测为负类数, 真反例,
所有情况加起来的总数为总的结果数.
T P + F N + F P + T N = 总 的 结 果 数 TP+FN+FP+TN=总的结果数 TP+FN+FP+TN=总的结果数.
混淆矩阵 Confusion matrix
| 实际数据 | 实际数据 | ||
|---|---|---|---|
| 实际为正类 | 实际为负类 | ||
| 预测结果 | 预测为正类 | TruePositive (with hit) | FalsePositive I 类错误 |
| 预测结果 | 预测为负类 | FalseNegative II 类错误 (with miss) | TrueNegative |
与统计学中的假设检验比较[5]
| H 0 H_0 H0 假设 | H 0 H_0 H0 假设 | ||
|---|---|---|---|
| 实际无效 | 实际为真 | ||
| 检验 | 判断为无效(reject H 0 H_0 H0) | TruePositive 1 − β 1-\beta 1−β | FalsePositive I 类错误 (弃真) α \alpha α |
| 检验 | 判断为真(Don’t reject H 0 H_0 H0) | FalseNegative II 类错误 (取伪) β \beta β | TrueNegative 1 − α 1-\alpha 1−α |
例
有13只动物 8 只猫 5 只狗
| 实际数据 | Dog | Cat | Cat | Dog | Cat | Cat | Dog | Cat | Cat | Dog | Dog | Cat | Cat |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 预测结果 | Dog | Dog | Cat | Dog | Cat | Cat | Dog | Cat | Dog | Cat | Cat | Dog | Cat |
| 实际数据 | 实际数据 | ||
|---|---|---|---|
| Cat | Dog | ||
| 预测结果 | 预测为Cat | 5 | 2 |
| 预测结果 | 预测为Dog | 3 | 3 |
5 + 3 + 2 + 3 = 13 5+3+2+3=13 5+3+2+3=13
confusion marix
| 实际数据 | 实际数据 | ||
|---|---|---|---|
| Cat | Non-Cat | ||
| 预测结果 | 预测为Cat | TruePositive 5 (with hit) | FalsePositive I 类错误 2 |
| 预测结果 | 预测为Non-Cat | FalseNegative II 类错误 3 (with miss) | TrueNegative 3 |
查准率 Precision
所有预测为正类数的结果中确实是正类数的比例, 或者说预测的结果中确实是正类占结果中所有预测为正类数的比例.
预测结果中所有预测为正类数的结果: T P + F P TP+FP TP+FP.
P r e c i s i o n = T P T P + F P Precision=\frac{TP}{TP+FP} Precision=TP+FPTP
主要受一类错误的影响.
- 挑出的好西瓜中有多少是真正的好西瓜
- 检索出的用户感兴趣的信息中有多少是真正用户感兴趣的
查全率, 召回率 Recall
所有的确实是正类数的样本在结果中被预测为正类数的比例, 或者说预测为正类的数占所有真正正类数的比例.
实际中所有真正正类数: T P + F N TP+FN TP+FN.
R e c a l l = T P T P + F N Recall=\frac{TP}{TP+FN} Recall=TP+FNTP
主要受二类错误的影响.
- 所有真正的好西瓜有多少被挑出来了
- 所有用户感兴趣的信息有多少被检索出来了
信息检索示例图示
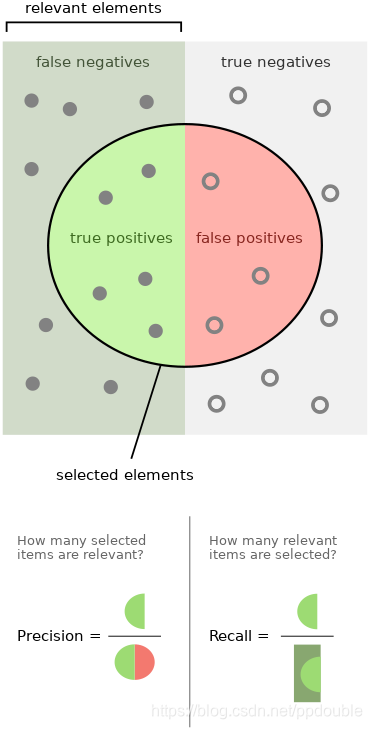
如何实现
学习器为测试样本产生一个实值或概率预测, 然后将这个预测概率值与一个分类阈值比较, 若大于阈值则分为正类, 否则分为反类. 若更重视查准率, 则阈值大一点, 则概率较大的为正例. 若更重视查全率, 则阈值小一点, 让那些更不可能是正类的样本, 即概率小的样本也划成正类. 也可以把预测概率值进行排序, 阈值作为截断点. 截断点前面作为正类. 后面作为反类. 可以想像成一个数值段, 截断点偏左端或者偏右端.
于是, 查准率大了查全率会小. 查准率小了查全率会大. 比如西瓜打分, 分越大瓜越好. 如果要高查准率则要选打分较高的那一部分, 即打分的有序降序序列上截断点靠左, 减少了一类错误假阳数, 更准确, 更有把握获得好瓜, 但是增加了二类错误假反例, 有一些好瓜可能被分为反类, 降低了查全率. 同样如果截断值较小, 靠有序降序分数右端, 好瓜基本上都被分类正类, 减少了二类错误把正类预测为负类的概率, 提高了查全率. 但是增加了一类错误假阳性判例, 降底了查准率.
综合查全率和查准率
-
希望有较高的查准率同时有较高的查全率, 即查的准又查的全.
-
倾向于高准确率
商品推荐系统中, 为了尽可能打扰用户, 希望推荐用户感兴趣的, 希望高准确率 -
倾向于高查全率
逃犯信息检索系统中, 希望尽可能少漏掉逃犯, 希望高的查全率
F 1 F1 F1 综合考虑查全率和查准率
对于第一种要综合查全率和查准率来考虑. 则使用调和平均数进行表示.
F 1 = 2 × P × R P + R F1=\frac{2\times P\times R}{P+R} F1=P+R2×P×R
F β F_\beta Fβ 侧重于查全率或查准率
对于第二种和第三种有所侧重的情况, 对二者使用加权调和平均. 权重分别为 α \alpha α, 1 − α 1-\alpha 1−α.
F α = α + 1 − α α P + 1 − α R = 1 α P + 1 − α R = 1 α R + ( 1 − α ) P P R = P R α R + ( 1 − α ) P F_\alpha = \frac{\alpha+1-\alpha}{\frac{\alpha}{P}+\frac{1-\alpha}{R}}=\frac{1}{\frac{\alpha}{P}+\frac{1-\alpha}{R}}=\frac{1}{\frac{\alpha R+(1-\alpha)P}{PR}}=\frac{PR}{\alpha R +(1-\alpha)P} Fα=Pα+R1−αα+1−α=Pα+R1−α1=PRαR+(1−α)P1=αR+(1−α)PPR
令 α = 1 1 + β 2 \alpha=\frac{1}{1+\beta^2} α=1+β21, β > 0 \beta>0 β>0, 0 < α < 1 0<\alpha< 1 0<α<1,
F β = F α = 1 1 + β 2 = P R 1 1 + β 2 R + ( 1 − 1 1 + β 2 ) P = ( 1 + β 2 ) P R β 2 P + R F_\beta=F_{\alpha=\frac{1}{1+\beta^2}}=\frac{PR}{\frac{1}{1+\beta^2} R +(1-\frac{1}{1+\beta^2})P}=\frac{(1+\beta^2)PR}{\beta^2P+R} Fβ=Fα=1+β21=1+β21R+(1−1+β21)PPR=β2P+R(1+β2)PR
又或者 ( 1 + β 2 ) P R β 2 P + R = 1 + β 2 1 P + β 2 R \frac{(1+\beta^2)PR}{\beta^2P+R}=\frac{1+\beta^2}{\frac{1}{P}+\frac{\beta^2}{R}} β2P+R(1+β2)PR=P1+Rβ21+β2, 相当于权重分别为: 1 1 1, β 2 \beta^2 β2
当
β
=
1
\beta=1
β=1,
α
=
1
2
\alpha=\frac{1}{2}
α=21,
F
α
=
1
2
=
F
1
F_{\alpha=\frac{1}{2}}=F1
Fα=21=F1
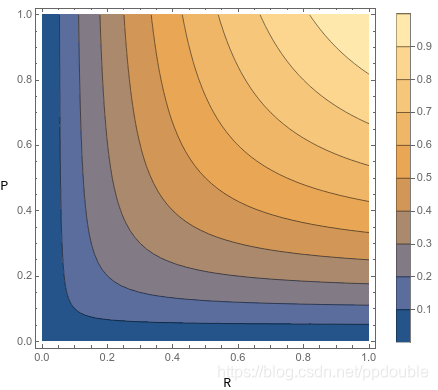
β
<
1
\beta<1
β<1, 则
α
>
1
2
\alpha>\frac{1}{2}
α>21, 查准率
P
P
P 的权重较大, 因此受查准率影响更大.
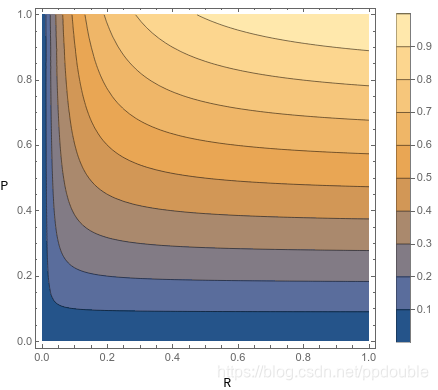
β
>
1
\beta>1
β>1, 则
α
<
1
2
\alpha<\frac{1}{2}
α<21, 查全率
R
R
R 的权重较大, 因此受查全率影响更大.
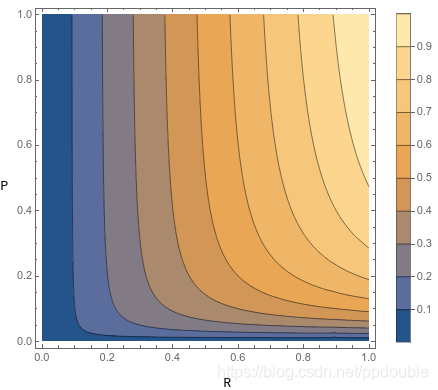
又或者找一个效率函数
E
=
E
(
P
,
R
)
E = E(P, R)
E=E(P,R)综合考虑查全率和查准率
构造
E
E
E, 使得
∂
E
∂
P
=
∂
E
∂
R
\frac{\partial E}{\partial P}=\frac{\partial E}{\partial R}
∂P∂E=∂R∂E,
E
E
E综合考虑查全率和查准率,
P
P
P,
R
R
R 对于
E
E
E 的变化是一样的.
构造 E = 1 − 1 α 1 P + ( 1 − α ) 1 R , 0 ≤ α ≤ 1 E=1-\frac{1}{\alpha\frac{1}{P}+(1-\alpha)\frac{1}{R}}, 0\leq \alpha \leq 1 E=1−αP1+(1−α)R11,0≤α≤1
更具体地, 令
α
=
1
1
+
β
2
\alpha=\frac{1}{1+\beta^2}
α=1+β21;
β
→
∞
,
α
→
0
\beta\rightarrow\infty, \alpha\rightarrow 0
β→∞,α→0;
β
→
0
,
α
→
1
\beta\rightarrow 0, \alpha\rightarrow 1
β→0,α→1
E
=
1
−
(
1
+
β
2
)
P
R
β
2
P
+
R
E=1-\frac{(1+\beta^2)PR}{\beta^2 P + R}
E=1−β2P+R(1+β2)PR
∵
\because
∵
∂
E
∂
P
=
−
(
1
+
β
2
)
R
2
(
β
2
P
+
R
)
2
\frac{\partial E}{\partial P}=-\frac{(1+\beta^2)R^2}{(\beta^2 P+R)^2}
∂P∂E=−(β2P+R)2(1+β2)R2,
∂
E
∂
R
=
−
(
1
+
β
2
)
β
2
P
2
(
β
2
P
+
R
)
2
\frac{\partial E}{\partial R}=-\frac{(1+\beta^2)\beta^2P^2}{(\beta^2 P+R)^2}
∂R∂E=−(β2P+R)2(1+β2)β2P2;
∂
E
∂
P
/
∂
E
∂
R
=
R
2
β
2
P
2
\frac{\partial E}{\partial P}/\frac{\partial E}{\partial R}=\frac{R^2}{\beta^2 P^2}
∂P∂E/∂R∂E=β2P2R2
∴
\therefore
∴ 当
R
P
=
β
\frac{R}{P}=\beta
PR=β 时,
∂
E
∂
P
=
∂
E
∂
R
\frac{\partial E}{\partial P}=\frac{\partial E}{\partial R}
∂P∂E=∂R∂E
此也用于
R
R
R 是
β
\beta
β 倍的
P
P
P时的综合评价结果, 对查全率的重视程度是查准率的
β
\beta
β 倍.
Ref.
[1] 李航 统计学习 第一版
[2] 周志华 机器学习
[3] 浙江大学 概率论与数理统计 第三版
[4] https://en.wikipedia.org/wiki/Precision_and_recall
[5] https://en.wikipedia.org/wiki/Type_I_and_type_II_errors
[6] https://www.statisticshowto.datasciencecentral.com/false-positive-definition-and-examples/
[7] https://www.statisticshowto.datasciencecentral.com/probability-and-statistics/statistics-definitions/type-i-error-type-ii-error-decision/
[8] https://en.wikipedia.org/wiki/Null_hypothesis
[9] https://blog.youkuaiyun.com/Tomxiaodai/article/details/81836769
[10]1995 Rijsbergen. Information Retrieval






















 8721
8721

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








