练车加端盘子也挡不住我学习系列——归并排序算法

什么是归并排序？

归并排序，是创建在归并操作上的一种有效的排序算法，效率为O(nlogn)。1945年由约翰·冯·诺伊曼首次提出。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用，且各层分治递归可以同时进行。速度仅次于快速排序，为稳定排序算法，一般用于对总体无序，但是各子项相对有序的数列，归并排序的比较次数小于快速排序的比较次数，移动次数一般多于快速排序的移动次数。你懂了吗？哈哈哈（手动滑稽~）

经典案例

我给你一个无序的数组，让你给我排序成从小到大的数组！你怎么排？
选择排序法？

for(int i=0;i<n-1;i++)
    	for(int j=i+1;j<n;j++)
    	{
    		if(a[i]>a[j])
    		{
    			int t;
    			t=a[i];
    			a[i]=a[j];
    			a[j]=t;
    		}
    	}

时间复杂度为O(n^2)，咱说，多少有点low啊，哈哈哈哈嗝。

归并排序算法

从早上10点练完车开始思考这个问题，中午端盘子，下午练车也在思考，现在才勉强能理解，但理解的还很不到位。这个算法对新手真的是不太友好。需要慢慢去捂，怎么实现的呢，看下面这个图！

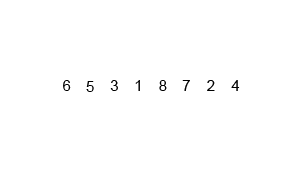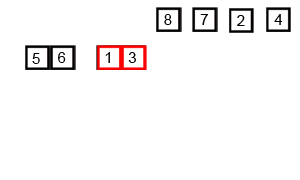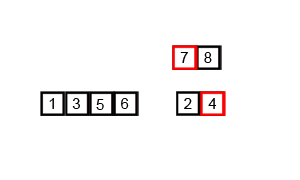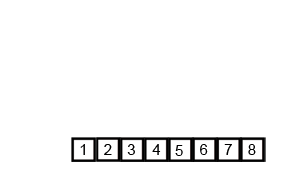
归并排序原来就是将一堆数字分开，再合成有序的数列。
其实，这就是分治的思想，将大问题化小问题，将每个最小的问题处理好，合并起来大问题也就处理OK了。

代码实现

#define Max 100
    void merge(int A[],int L1,int R1,int L2,int R2)//合并序列
    {
    	int i=L1,j=L2;
    	int temp[Max],counts=0;
    	while(i<=R1&&j<=R2)
    	{
    		if(A[i]<=A[j]) temp[counts++]=A[i++];
    		else temp[counts++]=A[j++];
    	}
    	while(i<=R1) temp[counts++]=A[i++];
    	while(j<=R2) temp[counts++]=A[j++];
    	for(int i=0;i<counts;i++)
    		A[L1+i]=temp[i];
    }
    void mergeSort(int A[],int left,int right)
    {
    	int mid;
    	if(left<right)
    	{
    		mid=(left+right)/2;
    		mergeSort(A,left,mid);//递归,对左边序列进行拆分
    		mergeSort(A,mid+1,right);//递归,对右边序列进行拆分
    		merge(A,left,mid,mid+1,right)//合并序列
    	}
    }

不懂就慢慢悟吧，俺也一样。