研习代码 day32 | 贪心策略终结——单调递增的数字 && 监控二叉树-优快云博客

一、单调递增的数字

1.1 题目

当且仅当每个相邻位数上的数字 x 和 y 满足 x <= y 时，我们称这个整数是单调递增的。

给定一个整数 n ，返回小于或等于 n 的最大数字，且数字呈 单调递增 。

示例 1:

输入: n = 10
输出: 9

示例 2:

输入: n = 1234
输出: 1234

示例 3:

输入: n = 332
输出: 299

提示:

0 <= n <= 10^9

1.2 题目链接

738.单调递增的数字

1.3 解题思路和过程想法

（1）解题思路

暴力解法：从 n 开始倒推判断，判断当前数是不是符合“单调递增”
整数转成字符串：从数字的每位数进行判断处理，从后往前遍历处理字符串：如果当前字符大于前一字符，则前一字符 -1 ，flag 置为当前位置（flag 标记需处理为9的初始位置，若只是将当前位置置为'9'，后面的数字不一定是最大的，例如 1000 ---> 900）。

（2）过程想法

暴力解法最好向，但会提示超时；整数转字符串的方法，思路不难，但是需注意 flag 的妙用。

1.4 代码

1.4.1 暴力解法（提示超时）

class Solution:
    # 判断当前数是不是符合“单调递增”
    def isValid(self,n) -> bool:
        num = n
        last = num % 10
        while num:
            if num % 10 > last:
                return False
            last = num % 10
            num = num // 10
        return True
    
    def monotoneIncreasingDigits(self, n: int) -> int:
        # 暴力解法：从 n 开始倒推判断
        for i in range(n,-1,-1):
            if self.isValid(i):
                return i

1.4.2 转成字符串

class Solution:   
    def monotoneIncreasingDigits(self, n: int) -> int:
        # 从 n 开始倒推判断的暴力解法会超时，故而借用字符串来进行判定
        # python 中不能修改字符串，故而将其转为列表
        s = list(str(n))

        # 标记需处理为9的初始位置
        flag = len(s)

        # 从后往前遍历处理字符串：如果当前字符大于前一字符，则前一字符 -1 ，flag 置为 当前位置
        for i in range(len(s)-1,0,-1):
            if s[i-1] > s[i]:
                s[i-1] = str(int(s[i - 1]) - 1)
                flag = i        # 若只是将当前位置置为'9'，后面的数字不一定是最大的，例如 1000 ---> 900

        # 将 flag 后的所有字符置为'9'   
        for i in range(flag,len(s)):
            s[i] = '9'

        return int(''.join(s))

二、监控二叉树

2.1 题目

给定一个二叉树，我们在树的节点上安装摄像头。

节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。

计算监控树的所有节点所需的最小摄像头数量。

示例 1：

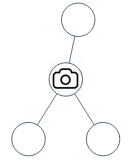
输入：[0,0,null,0,0]
输出：1
解释：如图所示，一台摄像头足以监控所有节点。

示例 2：

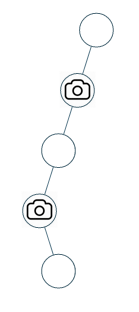
输入：[0,0,null,0,null,0,null,null,0]
输出：2
解释：需要至少两个摄像头来监视树的所有节点。 上图显示了摄像头放置的有效位置之一。

提示：

给定树的节点数的范围是 [1, 1000]。
每个节点的值都是 0。

2.2 题目链接

968.监控二叉树

2.3 解题思路和过程想法

（1）解题思路

从下往上遍历节点，根据左右孩子的情况，判断当前节点的情况。
                # 0：该节点未被覆盖
        # 1：该节点有摄像头
        # 2：该节点有被覆盖
        # 因叶子节点的父亲才有覆盖且有摄像头，所以空节点被视为有覆盖，但没有摄像头
        # 如果左右子树都被覆盖，则根节点不需被覆盖
        # 如果左右子树中至少有一个没有被覆盖，则根节点需加一个摄像头：(0,1)、(1,0)、(2,0)、(0,2)、(0,0)
        # 如果左右子树至少有一个仅被覆盖，则根节点为已覆盖（经过上述判断之后，这只会有(1,2)、(2,1)、(1,1)）

（2）过程想法

有后序遍历的想法，但是没有具有处理的思路。

2.4 代码

class Solution:
    def dfs(self,node,camera_count) ->int:
        # 因叶子节点的父亲才有覆盖且有摄像头，所以空节点被视为有覆盖，但没有摄像头
        if not node:
            return 2

        left = self.dfs(node.left,camera_count)   # 递归遍历左子树
        right = self.dfs(node.right,camera_count)   # 递归遍历右子树

        if left == 2 and right == 2: # 如果左右子树都被覆盖，则根节点不需被覆盖
            return 0   

        if left == 0 or right == 0: # 如果左右子树中至少有一个没有被覆盖，则根节点需加一个摄像头：(0,1)、(1,0)、(2,0)、(0,2)、(0,0)
            camera_count[0] += 1   
            return 1   

        if left == 1 or right == 1: # 如果左右子树至少有一个仅被覆盖，则根节点为已覆盖（经过上述判断之后，这只会有(1,2)、(2,1)、(1,1)）
            return 2

    def minCameraCover(self, root: Optional[TreeNode]) -> int:
        # 从下往上：后序遍历

        camera_count = [0]   # 初始摄像头数量为0

        # 0：该节点未被覆盖
        # 1：该节点有摄像头
        # 2：该节点有被覆盖
           
        result = self.dfs(root,camera_count)

        if result == 0 :      # 若根节点没有被覆盖
            return camera_count[0]+1
        else:
            return camera_count[0]           # 返回最终的摄像头数量