以下给出的均较为高效的算法
1.1字符串的旋转
题目描述:给出一个字符串,,将前面的若干个字符移到字符串的尾部,例如:“abcdef”的前3个字符‘a’、‘b’、‘c’移到字符串的尾部,那么原字符串将变成“defabc”。
算法描述:将原字符串分为X和Y两个部分,其中X为“abc”,Y为“def”,分别将X和Y进行翻转,X为“cba”。最后,将整个字符串进行翻转。得出结果。
参考代码如下:
void ReverseString(char* s,int from,int to){
while(from<to){
char t=s[from];
s[from]=s[to];
s[to]=t;
from++;
to--;
}
}
void LeftRotateString(char* s,int n,int m){
ReverseString(s,0,m-1);
ReverseString(s,m,n-1);
ReverseString(s,0,n-1);
}
时间复杂度:O(n),,空间复杂度:O(1)
1.2字符串的包含
题目描述:给定一长字符串a和一短字符串b,请问如何快速地判断出短字符串是否在长字符串中,例如字符串a是“ABCD”,字符串是“AA”,答案是true,否则为false。
算法描述:排序后轮询(很多算法进过排序都会降低时间复杂度)
代码如下:
bool StringContain(string &a,string &b){
sort(a.begin(),a.end());
sort(b.begin(),b.end());
for(int pa=0,pb=0;pb<b.length();){
while((pa<a.length())&&(a[pa]<b[pb])){
++p;
}
if((pa>=a.length())||(a[pa]>b[pb]))
{
return false;
}
++pb;
}
return true;
}
算法时间复杂度:O(mlogm)+O(nlogn)+O(m+n)
方法二:素数相乘
算法描述:首先,让长字符串a中的每个字母与一个素数一一对应,如a对应2,b对应3,c对应5,以此类推,遍历a,把a中的每个字母对应的素数相乘,得到一个整数,,然后,让短字符串也对应一个整数,再用a除以b如果结果有余数,结果为false,如果没有余数,结果为true,b为a的子集。
bool StringContain(string &a,string &b)
{
const int p[26]={2,3,5,7,11,13,17,19,23,29,31,37}; // 太多了,自己补吧
int f=1;
for(int i=0;i<a.length();i++){
int x=p[a[i]-'A'];
if(f%x){
f=f*x;
}
}
for(int i=0;i<b.length();i++){
int x=p[b[i]-'A'];
if(f%x){
return false;
}
}
return true;
}
这种算法的思想很好,实际上是不能运行的,因为素数的相乘的结果会很大,从而导致整数溢出,long long可以表示前16位。算法时间复杂度位O(m+n)。
1.3 字符串全排列-递归实现
算法思考
根据递归的特点,深度划分子逻辑-递归,标识出口。全排列一个思维:对待全排序的序列中从左选定一个数作为基数,然后对他右边的数进行全排列,以此递归。
算法描述
以字符串1234为例:
1 – 234
2 – 134
3 – 214
4 – 231
如何保证不遗漏: 每次递归前,保证1234的顺序不变。
算法演进
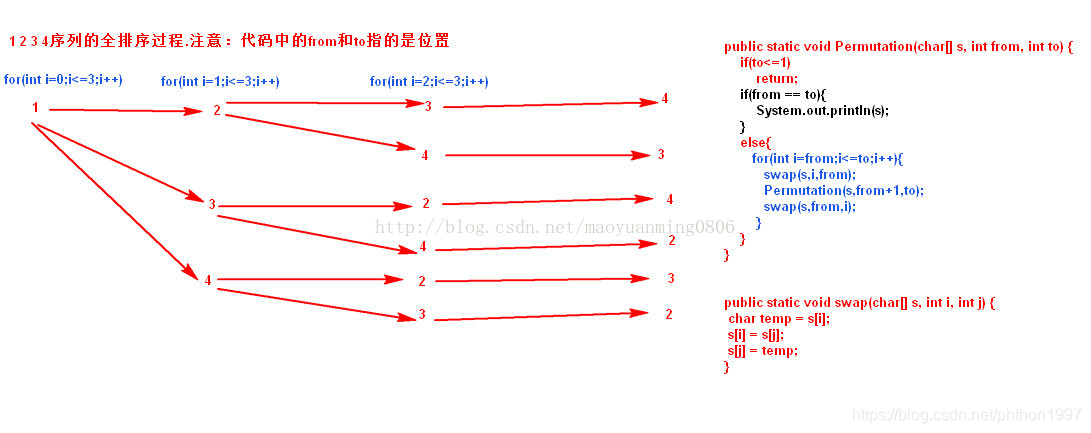
如1234序列,其中from和to指的是待全排序序列的首位置和尾位置。位置参考的是原序列长度
第一次就是from 0 to 3的全排列,选定1为基数,逐一的与后面序列每个数交换就得到以它为首的全部全排序序列,234就是进行 子全排列;然后在子全排列序列中就是from 1 to 3的全排列,选定2作为基数,34就是继续进行的 子全排列;然后在34中就是from 2 to 3的全排列,选定3为基数,4就是继续进行的 子全排列;…这时递归的深度会变大
当from == to相等时,自然不需要交换,全排序序列只有一个就是他自己,此时打印就好,此时return,递归就会往回走,然后根据循环走其他分支递归,直到没有分支递归,本层递归结束继续向上走。
void qpl(char* perm,int from,int to){
if(to<=1){ // 第一个不用动的
return;
}
if(from==to){
for(int i=0;i<=to;i++){
cout<<perm[i];
}
cout<<endl;
}
else{
for(int j=from;j<=to;j++){
swap(perm[j],perm[from]);
qpl(perm,from+1,to);
swap(perm[j],perm[from]);
}
}
}




 本文介绍三种高效的字符串操作算法,包括字符串旋转、字符串包含检测及字符串全排列。详细解析了每种算法的实现原理,提供了代码示例,并分析了时间与空间复杂度。
本文介绍三种高效的字符串操作算法,包括字符串旋转、字符串包含检测及字符串全排列。详细解析了每种算法的实现原理,提供了代码示例,并分析了时间与空间复杂度。
















 272
272

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








