Cheapest Flights Within K Stops

[leetcode]Cheapest Flights Within K Stops

链接：https://leetcode.com/problems/cheapest-flights-within-k-stops/description/

Question

There are n cities connected by m flights. Each fight starts from city uand arrives at v with a price w.

Now given all the cities and fights, together with starting city src and the destination dst, your task is to find the cheapest price from src to dst with up to k stops. If there is no such route, output -1.

Example 1

Input: 
n = 3, edges = [[0,1,100],[1,2,100],[0,2,500]]
src = 0, dst = 2, k = 1
Output: 200
Explanation: 
The graph looks like this:

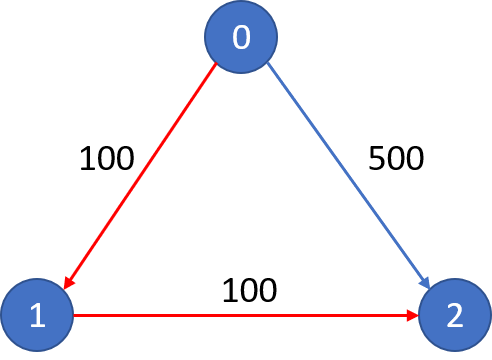
The cheapest price from city 0 to city 2 with at most 1 stop costs 200, as marked red in the picture.

Example 2

Input: 
n = 3, edges = [[0,1,100],[1,2,100],[0,2,500]]
src = 0, dst = 2, k = 0
Output: 500
Explanation: 
The graph looks like this:

The cheapest price from city 0 to city 2 with at most 0 stop costs 500, as marked blue in the picture.

Note:

• The number of nodes n will be in range [1, 100], with nodes labeled from 0 to n`` - 1.
• The size of flights will be in range [0, n * (n - 1) / 2].
• The format of each flight will be (src, ``dst``, price).
• The price of each flight will be in the range [1, 10000].
• k is in the range of [0, n - 1].
• There will not be any duplicated flights or self cycles.

Solution

class Solution {
public:
  #define offset 10
  #define inf 0x3fffffff
  struct headnode {
    int node, dist, p;
    headnode(int n, int d, int p_): node(n), dist(d), p(p_) {}
    bool operator<(const headnode& another) const { return dist > another.dist; }
  };

  int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int K) {

    vector<vector<int> > d;
    d.resize(120, vector<int>());
    for (int i = 0; i < 120; i++) d[i].resize(120, inf);

    priority_queue<headnode> pq;
    d[src][-1+offset] = 0;
    pq.push(headnode(src, d[src][0], -1));
    while (!pq.empty()) {
      headnode top = pq.top(); pq.pop();
      int node = top.node;
      int p = top.p;
      if (p >= K) continue;
      for (int i = 0; i < flights.size(); i++) {
        if (flights[i][0] == node) {
          int another = flights[i][1];
          int dist = flights[i][2];
          if (d[another][p+1+offset] > d[node][p+offset]+dist) {
            d[another][p+1+offset] = d[node][p+offset]+dist;
            pq.push(headnode(another, d[another][p+1+offset], p+1));
          }
        }
      }
    }
    int min_value = inf;
    for (int i = -1; i <= K; i++) 
      min_value = min(min_value, d[dst][i+offset]);
    if (min_value == inf) min_value = -1;
    return min_value;
  }
};

思路：这是一道最短路径改编的题目，需要在结点加入一个p来看当前节点处于哪个stop。而记录原来路径信息的dp[i]也变成了dp[i][p]，最后需要从同一个结点的小于等于K的所有stop中挑出最小的值就是结果了。