算法笔记-图的搜索

社交网络中，有一个六度分割理论，就是你跟世界任何一个人间隔的关系不会超过六度，也就是通过六步就能将你跟另一个陌生人连接起来。

对应到社交好友中，你的好友就是你的一度连接，你的好友的好友就是你的二度连接，你的好友的好友的好友就是你的三度连接。

对应用图存储的社交关系，找到你的一度二度三度好友就是在图中找到搜索相关的顶点。这就运用到图的搜索算法：深度优先和广度优先搜索。

图结构的代码实现

public class Graph {
	
	private int v; // 顶点的个数
	private LinkedList<Integer> adj[]; // 邻接表:数组中的元素是链表

	/**
	 * 初始化图结构
	 * @param v
	 */
	public Graph(int v) {
		this.v = v;
		adj = new LinkedList[v];
		for (int i = 0; i < v; ++i) {
			adj[i] = new LinkedList<>();
		}
	}

	/**
	 * 构建图中顶点的关系，
	 * 该结构实现的是无向图，
	 * 所以需要给两个顶点的链表中都存储对方
	 * @param s
	 * @param t
	 */
	public void addEdge(int s, int t) {
		adj[s].add(t);
		adj[t].add(s);
	}
}

上述代码中，初始化图的时候，构建一个以顶点个数为长度的数组，同时初始化数组中的元素都是链表。

广度优先搜索

广度优先搜索简称 BFS，是一种地毯式搜索算法。对给定顶点，先搜索与之关联的顶点，然后搜索与之关联顶点相关联的顶点，直至最后搜索到需要查找的顶点。图例如下：

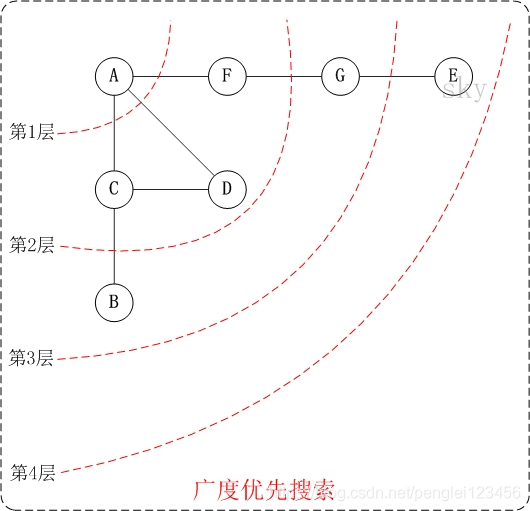
代码实现如下：

	/**
	 * 广度优先搜索
	 * @param s
	 * @param t
	 */
	public void bfs(int s, int t) {
		//开始顶点和结束顶点是一个顶点
		if (s == t){
			return;
		}
		//记录访问过的顶点，访问过用 true 表示
		boolean[] visited = new boolean[v];
		visited[s] = true;
		//待访问顶点的队列，先加入开始顶点
		Queue<Integer> queue = new LinkedList<>();
		queue.add(s);
		//记录每个顶点是通过哪一个顶点访问过来的，
		//如果该顶点被访问了，数组中存储上一个顶点的下标,否则存储-1
		int[] prev = new int[v];
		for (int i = 0; i < v; ++i) {
			prev[i] = -1;
		}
		//循环队列
		while (queue.size() != 0) {
			//出列
			int w = queue.poll();
			//遍历与该顶点关联的顶点
			for (int i = 0; i < adj[w].size(); ++i) {
				//获取下标
				int q = adj[w].get(i);
				//判断该顶点是否被访问
				if (!visited[q]) {
					//记录该顶点是被下标 w 的顶点访问过来的
					prev[q] = w;
					if (q == t) {
						//输出路径
						print(prev, s, t);
						return;
					}
					//记录顶点被访问
					visited[q] = true;
					//入列
					queue.add(q);
				}
			}
		}
	}
	
	/**
	 * 由于 pre 中记录的是访问该下标顶点的顶点下标，
	 * 所以路径是一个逆向过程，需要利用递归找到完整的路径 
	 * @param prev
	 * @param s
	 * @param t
	 */
	private void print(int[] prev, int s, int t) { // 递归打印 s->t 的路径
		//不是开始节点，并且该节点被访问
		if (prev[t] != -1 && t != s) {
			print(prev, s, prev[t]);
		}
		System.out.print(t + " ");
	}

代码中有着详细的注释，额外再补充以下几点：visited 用来判断该顶点是否被访问过，queue 中存储需要访问的顶点，prev 中存储连接到顶点的上个顶点下标。

代码执行过程示例：

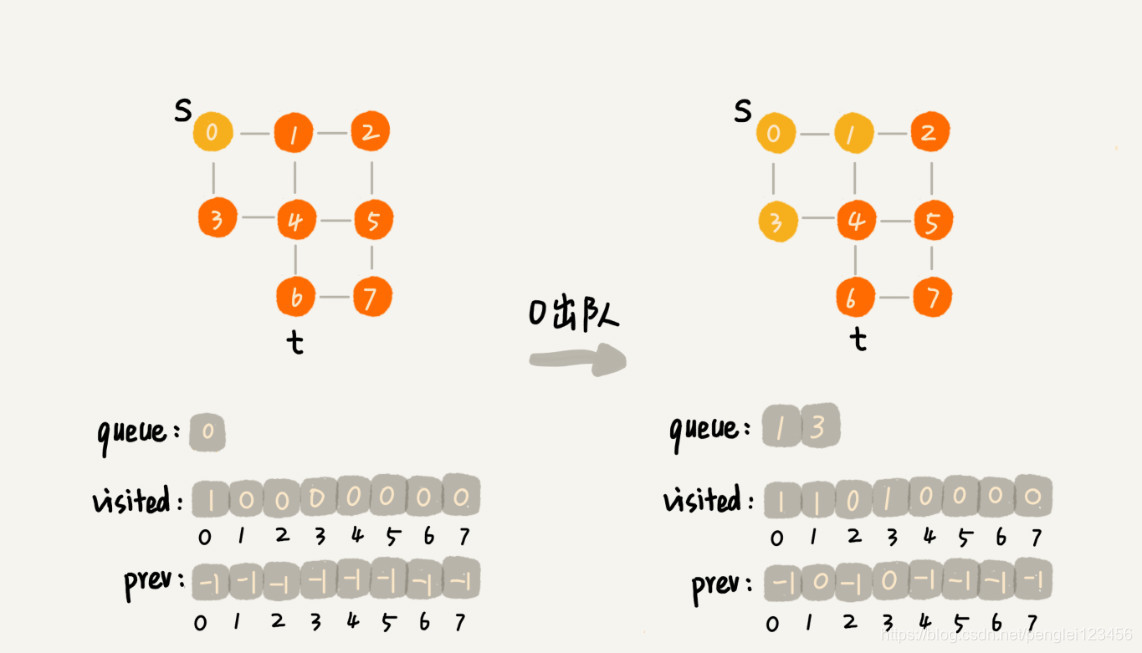
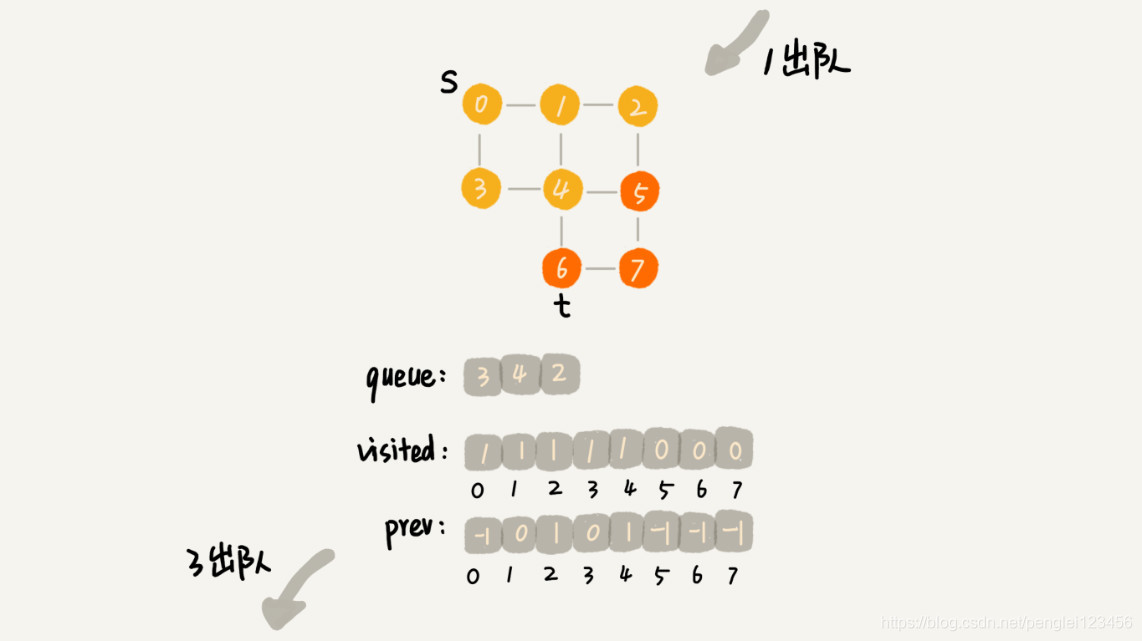
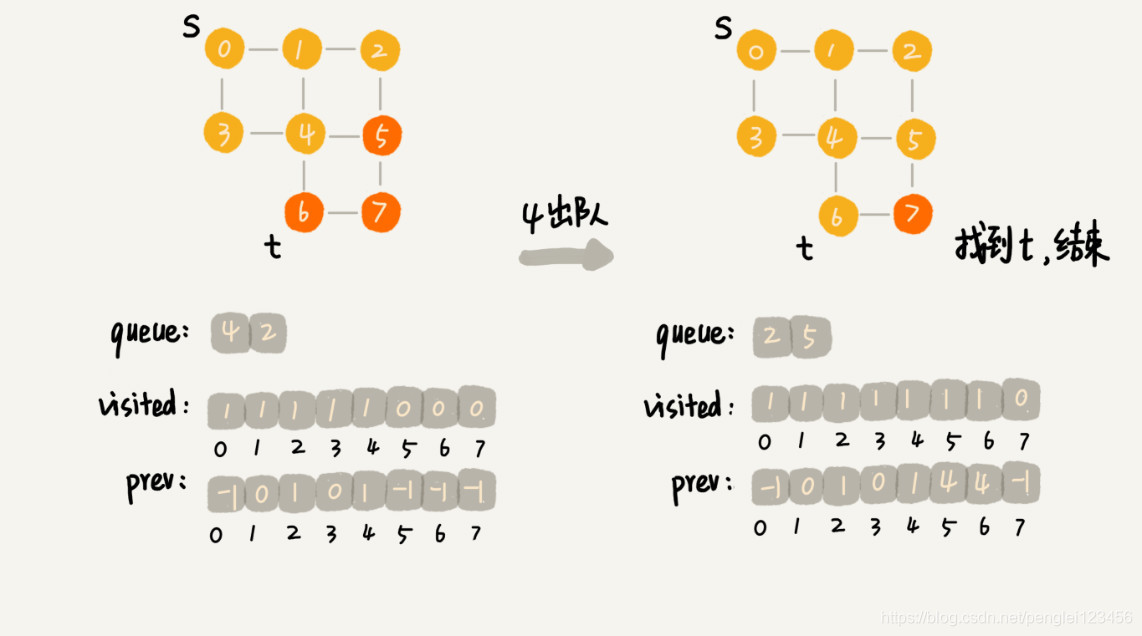
广度优先搜索中时间复杂度：从 s 顶点到 t 顶点 ，每个顶点都会被访问一次，每条边也会被访问一次。假如有 n 个顶点，边数最多为 n - 1，所以时间复杂度为 O(n)。visited，queue，prev 的内存不会超过 n，所以空间复杂度为 O(n)。

深度优先搜索

深度优先搜索，简称 DFS。

类似于走迷宫，在迷宫中遇到分叉路口，选择其中一条路走下去。如果走不通，则返回选择另外一条路，直至最后走出迷宫。

对于图，从开始顶点选择一条边访问另外一个顶点，如果该顶点后续没有边可选择，则原路返回，选择另一条边走，直至访问到要访问的顶点。

代码实现如下：

	// 标识变量 ture 停止搜索
	boolean found = false; // 全局变量或者类成员变量

	public void dfs(int s, int t) {
		found = false;
		// 初始化被访问数组
		boolean[] visited = new boolean[v];
		// 记录每个顶点是通过哪一个顶点访问过来的，
		// 如果该顶点被访问了，数组中存储上一个顶点的下标,否则存储-1
		int[] prev = new int[v];
		for (int i = 0; i < v; ++i) {
			prev[i] = -1;
		}
		// 调用深度优选搜索
		recurDfs(s, t, visited, prev);
		// 输出路径
		print(prev, s, t);
	}

	/**
	 * 
	 * @param w
	 * @param t
	 * @param visited
	 * @param prev
	 */
	private void recurDfs(int w, int t, boolean[] visited, int[] prev) {
		//判断是否搜索到顶点
		if (found == true){
			return;
		}
		// 下标 w 对应的顶点标记被访问
		visited[w] = true;
		// 找到要搜索的顶点，found 赋值为 true 结束递归
		if (w == t) {
			found = true;
			return;
		}
		for (int i = 0; i < adj[w].size(); ++i) {
			//获取下标 q 关联的顶点
			int q = adj[w].get(i);
			//判断是否被访问过
			if (!visited[q]) {
				//标记访问
				prev[q] = w;
				//从顶点 q 搜索顶点 t
				recurDfs(q, t, visited, prev);
			}
		}
	}

	/**
	 * 由于 pre 中记录的是访问该下标顶点的顶点下标， 所以路径是一个逆向过程，需要利用递归找到完整的路径
	 * 
	 * @param prev
	 * @param s
	 * @param t
	 */
	private void print(int[] prev, int s, int t) { // 递归打印 s->t 的路径
		// 不是开始节点，并且该节点被访问
		if (prev[t] != -1 && t != s) {
			print(prev, s, prev[t]);
		}
		System.out.print(t + " ");
	}

代码运行图例如下：

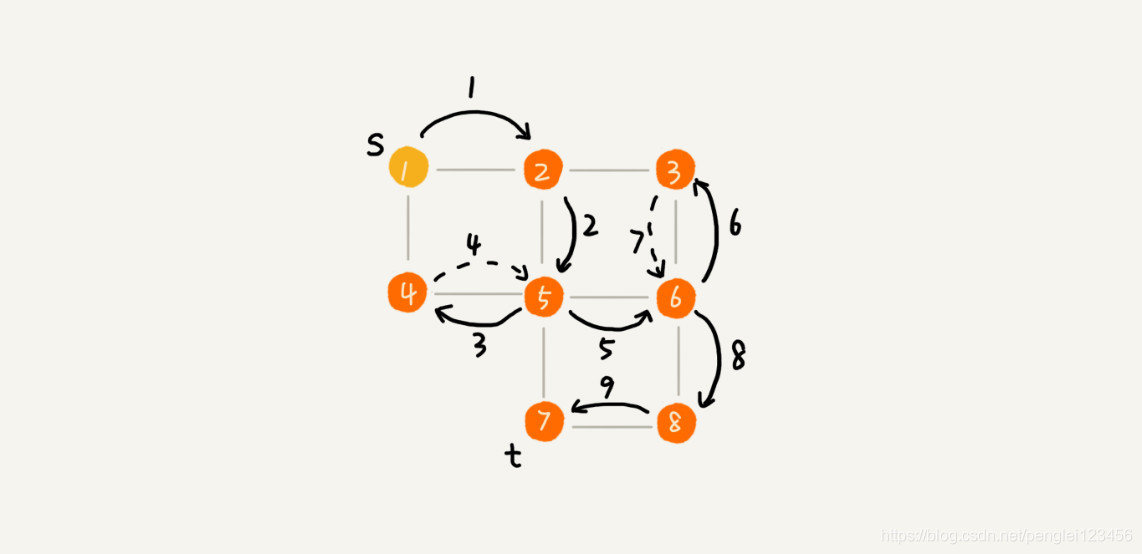
深度优先搜索的时间复杂度跟访问边的次数相关，每条边最多被访问两次，一次是正常访问，一次是返回。所以时间复杂度也是 O(n)，空间复杂度分析与广度优先搜索一样，都是 O(n)。深度优先搜索采用的是回溯思想，利用递归实现的搜索算法。

总结

本文创作灵感来源于 极客时间 王争老师的《数据结构与算法之美》课程，通过课后反思以及借鉴各位学友的发言总结，现整理出自己的知识架构，以便日后温故知新，查漏补缺。

初入算法学习，必是步履蹒跚，一路磕磕绊绊跌跌撞撞。看不懂别慌，也别忙着总结，先读五遍文章先，无他，唯手熟尔~
与诸君共勉

关注本人公众号，第一时间获取最新文章发布，每日更新一篇技术文章。