数据结构实验九：图的应用+线性查找_16.对22个记录的有序表作折半查找,当查找失败时,至少需要比较( )次关键字。-优快云博客

本节课实验课总体安排：

1、完成图的应用-深度优先遍历和广度优先遍历的习题讲解

2、两个班进度统一一下，把2班的理论课讲完分块查找

3、查找的算法设计讲解

一、图的应用之深度优先遍历和广度优先遍历习题

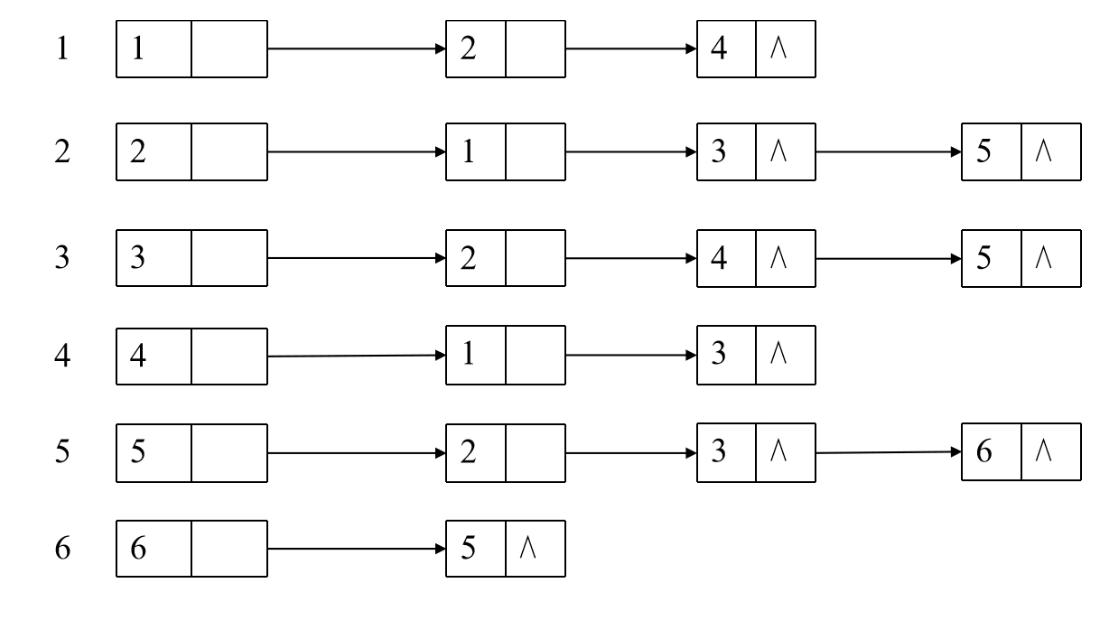
已知无向图G的邻接表如图 1 所示，分别写出从顶点 1 出发的深度优先遍历和广度优先遍历序列，并画出相应的生成树。

二、查找的算法设计题

1、（选择题）对22个记录的有序表作折半查找，当查找失败时，至少需要比较（）次关键宇。

A、3 B、4 C、5 D、6

对折半查找来说：

查找失败时，不同路径可能导致比较次数不同；
最少比较次数是最短路径的比较次数。
对 22 个元素的有序表：
- 最少比较次数 = 树高度的下限
- 二分查找对应的“完全二叉树”高度：
  ⌊log⁡2n⌋=4⌊log2n⌋=4
- 因此至少比较 4 次就能确定查找失败。

2、顺序查找算法设计

给定一个升序排列的整型数组nums = [-1, 0, 3, 5, 9, 12]，请编写一个使用折半查找（Binary Search）思想的函数，在数组中查找目标值 target所在的数组下标。

测试用例：

输入：9

输出：4

#include <stdio.h>

int binarySearch(int nums[], int n, int target) {
    int left = 0, right = n - 1;

    while (left <= right) {
        int mid = (left + right) / 2;
        if (nums[mid] == target) {
            return mid;
        } else if (nums[mid] < target) {
            left = mid + 1;
        } else {
            right = mid - 1;
        }
    }

    return -1;
}

int main() {
    int nums[] = {-1, 0, 3, 5, 9, 12};
    int n = sizeof(nums) / sizeof(nums[0]);
    int target;

    scanf("%d", &target);

    int result = binarySearch(nums, n, target);

    printf("%d", result);

    return 0;
}

三、代码讲解

顶层说明（先把整体意图说清楚）

这个程序实现的是折半查找（Binary Search）：在一个升序排列的整型数组 nums 中寻找 target，若找到返回对应下标（从 0 起），找不到返回 -1。主函数 main 固定给出数组并从标准输入读入 target，binarySearch 函数完成查找并返回结果，main 将结果打印到标准输出。

逐行讲解与原因

#include <stdio.h>

功能：包含标准输入输出库，使得程序可以使用 scanf、printf 等函数。
为什么要写：没有它 scanf/printf 等函数的声明不可用，编译会警告或失败。

int binarySearch(int nums[], int n, int target) {

功能：定义一个名为 binarySearch 的函数，返回 int（找到则返回下标，否则返回 -1）。
参数解释：
- int nums[]：要搜索的数组（在函数形参中，int nums[] 等价于 int *nums —— 数组名退化为指针）。
- int n：数组长度（因为数组在传入函数时退化为指针，函数内部无法通过 sizeof 得到长度，所以需要把长度传入）。
- int target：要查找的目标值。
为什么要分函数：把查找逻辑封装到函数里，便于重用、测试和理解；使 main 更清晰。

int left = 0, right = n - 1;

功能：初始化查找区间的左右边界索引：
- left 指向当前查找区间的左端（初始为 0，数组第一个元素）。
- right 指向当前查找区间的右端（初始为 n-1，数组最后一个元素）。
为什么这样：二分查找在有序数组上通过不断缩小 [left, right] 区间来定位目标，初始区间为整数组。

while (left <= right) {

功能：循环条件，表示当区间仍有元素时继续查找。
为什么是 <= 而不是 <：当 left == right 时区间仍包含一个元素，需要检查这个元素，所以用 <=。当 left > right 时，区间为空，查找结束。

int mid = (left + right) / 2;

功能：计算当前区间的中间下标 mid，把区间分为两半。
为什么要取中点：将有序区间对半分，二分查找的核心就是每步比较中点元素并根据大小决定舍弃哪一半，从而在对数时间内缩小范围。
注意与改进（溢出问题）：表达式 (left + right) 在极大数组索引情况下可能溢出（当 left + right 超过 int 上限）。更安全的写法是 int mid = left + (right - left) / 2;。
在本程序因为数组很小（定长 6），不会有实际问题，但教学时应指出这一点。

if (nums[mid] == target) {

功能：比较中间元素与目标值。
如果相等：找到了目标，返回 mid（下标）。

return mid;

功能：函数直接返回找到的下标，结束查找。
为什么直接返回：找到目标后无需继续查找，返回结果即可。

} else if (nums[mid] < target) {

功能：如果中点元素小于目标，表示目标（若存在）只能出现在中点右侧（因为数组升序）。
为什么这样判断：数组有序，若 nums[mid] < target，则左半部分（含 mid）都小于目标，可全部排除。

left = mid + 1;

功能：把左边界移动到 mid + 1，排除 mid 及其左侧元素，开始在右半区继续查找。
为什么是 mid + 1：mid 已确定不是目标（上一步比较），因此查找区间从 mid+1 开始。

} else {

否则（即 nums[mid] > target），目标（若存在）只能在左半区。

right = mid - 1;

功能：把右边界移动到 mid - 1，排除 mid 及其右侧元素，继续在左半区查找。
为什么是 mid - 1：mid 不是目标并且比目标大，所以 mid 及其右侧没有目标。

}

结束 if-else 分支。

}

结束 while 循环。循环会在 left > right（区间为空）或在函数中返回（找到了）时结束。

return -1;

功能：当循环结束但没有找到目标时返回 -1 表示失败。
为什么要返回 -1：约定失败返回一个不可能的合法下标（数组下标非负），-1 常用作未找到的标志。

}

结束 binarySearch 函数定义。

main 函数逐行解释

int main() {

程序入口。标准的 C 语言 main 函数。

int nums[] = {-1, 0, 3, 5, 9, 12};

功能：在程序中直接定义并初始化数组 nums，元素为题目指定的升序数组。
为什么固定数组在程序中：题目要求数组在代码中给定，不从输入读取。

int n = sizeof(nums) / sizeof(nums[0]);

功能：计算数组元素个数 n。
解释 sizeof：
- sizeof(nums) 返回数组占用的字节总数（例如 6 个 int，若 int 为 4 字节则为 24）。
- sizeof(nums[0]) 返回数组第一个元素的字节大小（即 int 的字节数）。
- 两者相除得到元素个数。
为什么在 main 可以用 sizeof：在定义数组的作用域（这里是 main）可以用 sizeof 得到整个数组的字节大小。但如果数组被当做参数传到函数（比如 binarySearch），在函数内 nums 已退化为指针，此时 sizeof(nums) 不能得到数组长度，因此必须在外部计算并传入 n。

int target;

声明整型变量 target，用来接收用户输入的查找值。

scanf("%d", &target);

功能：从标准输入读入一个整数并存入 target。
为什么用 scanf：题目要求“输入只包含数字”，所以直接读取整数即可；没有任何额外的提示输出，符合要求。
注意：scanf 返回成功读取值的个数，可用于更严格的错误检查（例如 if (scanf("%d", &target) != 1) { /* 处理输入错误 */ }）。本程序为简洁未加检查。

int result = binarySearch(nums, n, target);