剑指Offer(1)-[BinaryTree]重建二叉树

点击查看剑指Offer全解【Java & Golang】实现

题目描述

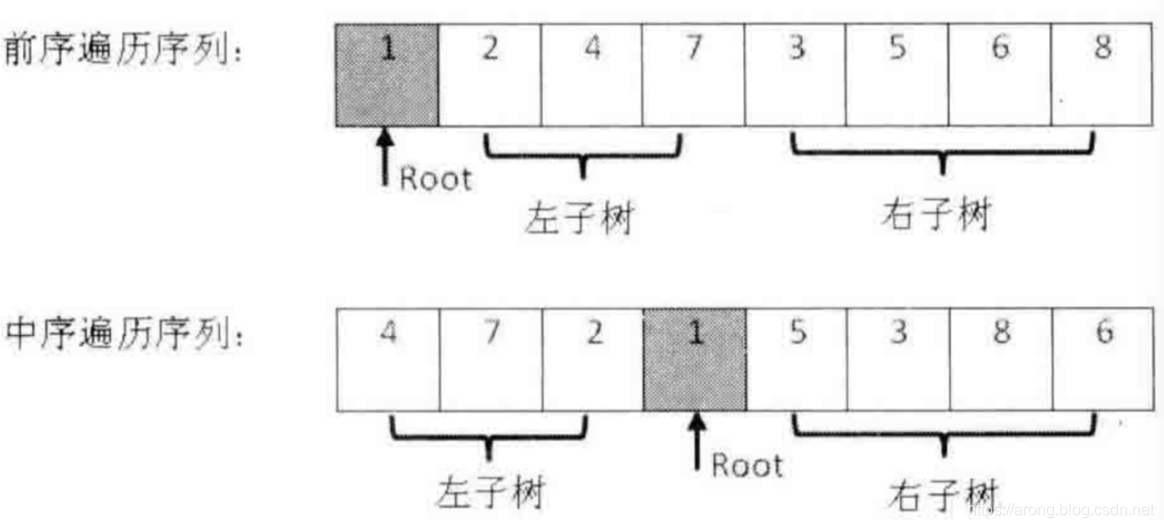
输入某二叉树的前序遍历和中序遍历的结果，请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}，则重建二叉树并返回。

---

思路

前序遍历：跟节点 + 左子树前序遍历 + 右子树前序遍历

中序遍历：左子树中序遍历 + 跟节点 + 右字数中序遍历

后序遍历：左子树后序遍历 + 右子树后序遍历 + 跟节点

根据上面的规律：

前序遍历找到根结点root
找到root在中序遍历的位置 -> 左子树的长度和右子树的长度 ->
截取左子树的中序遍历、右子树的中序遍历 ->
截取左子树的前序遍历、右子树的前序遍历 ->
递归重建二叉树

---

Java第一种做法【传递数组索引定位，高效，但比较复杂】

/**
 * Definition for binary tree
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
public class Solution {
    public TreeNode reConstructBinaryTree(int [] pre,int [] in) {
        return helper(pre, in, 0, pre.length - 1, 0, in.length - 1);
    }
    private TreeNode helper(int[] pre, int[] in, int preLeft, int preRight, int inLeft, int inRight) {
        // 
        if (preLeft > preRight || inLeft > inRight) {
            return null;
        }
        // 由前序遍历序列获取根节点
        int rootValue = pre[preLeft];
        TreeNode root = new TreeNode(rootValue);    
        // 在中序遍历序列中，搜索出根节点的位置
        int index = findRootIndex(rootValue, in);
        // 通过根节点位置，在中序遍历序列中可划分出左子树和右子树的中序遍历序列
        // 在前序遍历中，可划分出左子树和右子树的前序遍历序列,继续递归地构建树
        // preLeft + index - inLeft：通过preLeft + 左子树节点数（index - inLeft）确定左子树前序遍历的右边界
        // preLeft + index - inLeft + 1:通过左子树前序遍历序列的右边界+1确定右子树前序遍历序列的左边界
        root.left = helper(pre, in, preLeft + 1, preLeft + index - inLeft, inLeft, index - 1);
        root.right = helper(pre, in, preLeft + index - inLeft + 1, preRight, index + 1, inRight);
        return root;
    }
    private int findRootIndex(int target, int[] array) {
        for (int i = 0; i < array.length; i++) {
            if (array[i] == target) {
                return i;
            }
        }
        return -1;
    }
    
}

Java第二种做法 【使用Arrays工具类复制数组，比较占用空间，但简洁】

/**
 * Definition for binary tree
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
import java.util.Arrays;
public class Solution {
    public TreeNode reConstructBinaryTree(int [] pre,int [] in) {
        // 当前序遍历序列或后序遍历序列为空时，说明该节点为空节点
        if (pre.length == 0 || in.length == 0) {
            return null;
        }
        // 由前序遍历序列获取根节点
        int rootValue = pre[0];
        TreeNode root = new TreeNode(rootValue);
        // 在中序遍历序列中，搜索出根节点的位置
        int index = findRootIndex(rootValue, in);
        // 通过根节点位置，在中序遍历序列中可划分出左子树和右子树的中序遍历序列
        // 在前序遍历中，可划分出左子树和右子树的前序遍历序列,继续递归地构建树
        root.left = reConstructBinaryTree(
            Arrays.copyOfRange(pre, 1, index + 1),
            Arrays.copyOfRange(in, 0, index)
        );
        root.right = reConstructBinaryTree(
            Arrays.copyOfRange(pre, index + 1, pre.length),
            Arrays.copyOfRange(in, index + 1, in.length)
        );
        return root;
    }
    private int findRootIndex(int target, int[] array) {
        for (int i = 0; i < array.length; i++) {
            if (array[i] == target) {
                return i;
            }
        }
        return -1;
    }
}

Golang第一种做法

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func buildTree(pre []int, in []int) *TreeNode {
	return helper(pre, in, 0, len(pre) - 1, 0, len(in) - 1)
}
func helper(pre []int, in []int, preLeft int, preRight int, inLeft int, inRight int) *TreeNode{
	if preLeft > preRight || inLeft > inRight {
		return nil
	}
	var rootValue int = pre[preLeft]
	var root *TreeNode = &TreeNode{rootValue, nil, nil}
	var index = findRootIndex(rootValue, in)
	root.Left = helper(pre, in, preLeft + 1, preLeft + index - inLeft, inLeft, index - 1)
	root.Right = helper(pre, in, preLeft + index - inLeft + 1, preRight, index + 1, inRight)
	return root
}
func findRootIndex(target int, array []int) int{
	for i := 0; i < len(array); i++ {
		if array[i] == target {
			return i
		}
	}
	return -1
}

Golang第二种做法

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func buildTree(pre []int, in []int) *TreeNode {
	if len(pre) == 0 || len(in) == 0 {
		return nil
	}
	var rootValue int = pre[0]
	var root *TreeNode = &TreeNode{rootValue, nil, nil}
	var index = findRootIndex(rootValue, in)
	root.Left = buildTree(pre[1:index + 1], in[0:index])
	root.Right = buildTree(pre[index + 1:], in[index + 1:])
	return root
}
func findRootIndex(target int, array []int) int{
	for i := 0; i < len(array); i++ {
		if array[i] == target {
			return i
		}
	}
	return -1
}