剑指Offer(9)-位运算问题

最新推荐文章于 2024-04-17 21:01:23 发布

原创最新推荐文章于 2024-04-17 21:01:23 发布 · 379 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#位运算

编程基本功训练同时被 2 个专栏收录

70 篇文章

订阅专栏

计算机科学基础

54 篇文章

订阅专栏

本文深入探讨了位运算的基础知识及实用技巧，包括计算二进制中1的个数、判断整数是否为2的幂，以及计算两个整数转换所需的位变化数。通过具体的代码示例，详细解析了每种方法的实现原理与步骤。

文章目录

1.0 位运算相关

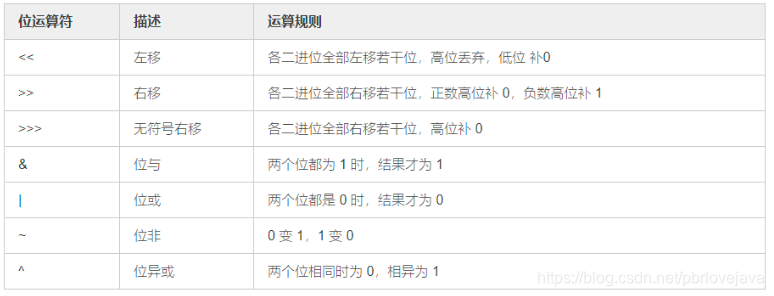
在这里插入图片描述

1.1 二进制中1出现的次数

第一个做法是将n和1做与运算，若这个数的最低位为1，那么结果为1；若最低位为0，则结果为0，所以在这里可以直接累加来获取末尾1的个数。之后需要将n无符号右移1位消去最低位的1或0，继续重复上述过程，直到n为0；。（为什么不使用有符号右移？当n为负数时，最高位符号位为1，那么在>>之后还会在最高位补1，造成n != 0这个条件永远成立）。这个做法需要循环的次数为n的位数。

public class Solution {
    public int NumberOf1(int n) {
        // >> 带符号右移位，当最高位为符号位且为 1时，右移补位的还是1,为0则补0:1001>>3 = 1111
        // >>> 不带符号的右移位，当最高符号位为1时，右移位补的还是0:1001>>>3 = 0001
        int res = 0;
        while (n != 0) {
            //和1做与运算，若最低位为1则结果为1，若最低位为0则结果为0
            res += n & 1;
            //n无符号右移一位
            n = n >>> 1;
        }
        return res;
    }
}

第二个做法是利用一个整数减去1之后在与原来的整数做与运算，得到的结果相当于二进制中最右边的1变为0，例如1010减去1得1001,1001 & 1010 = 1000,最右边的1变为了0这个性质来统计n中1的个数，这个做法的循环次数为n中含有1的位数。

public class Solution {
    public int NumberOf1(int n) {
        int res = 0;
       	while (n != 0) {
       		res ++;
       		n = (n - 1) & n;
       	}
        return res;
    }
}

1.2 判断一个整数是否为2的幂

如果一个数是2的次方，那么这个数的二进制数中只有一个1;利用 (n - 1) & n会将最右边的1变为0的特性，只需要判断这个数消去1后是否为0则可知道其是否为2的次方(0和负数除外)

class Solution {
    public boolean isPowerOfTwo(int n) {
        if (n <= 0) return false;
        return ((n - 1) & n) == 0;
    }
}

1.3 A改变多少次才能变为B

将整数A、B转化为二进制，请问A需要改变其中的几位才能够转化为B？
例如0110需要改变3位才能变为1000,这里就是异或即可：0110 ^ 1000 = 3

public class Solution {
    // you need to treat n as an unsigned value
    public int solve(int a, int b) {
        return a ^ b;
    }
}