Leetcode题解： LCP2 分式化简

最新推荐文章于 2020-08-21 13:52:03 发布

原创最新推荐文章于 2020-08-21 13:52:03 发布 · 341 阅读

CC 4.0 BY-SA版权

本文介绍了如何解决LeetCode上的LCP2问题，即分式化简。通过将连分数转化为不断计算ax+1/(n/m)的形式，并从an-1开始递推，最终使用辗转相除法求得最简分数[n, m]，确保其最大公约数为1。" 16946095,1321511,理解编译原理：正则表达式与词法分析,"['正则表达式', '编译原理', '编程语言', '词法分析']

题目描述

有一个同学在学习分式。他需要将一个连分数化成最简分数，你能帮助他吗？

连分数是形如上图的分式。在本题中，所有系数都是大于等于0的整数。

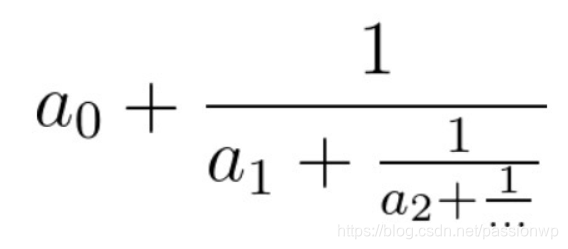
在这里插入图片描述

输入的cont代表连分数的系数（cont[0]代表上图的a0，以此类推）。返回一个长度为2的数组[n, m]，使得连分数的值等于n / m，且n, m最大公约数为1。

解题思路

首先将计算连分数过程抽象为不断计算ax+1/(n/m)的过程。以an-1为起点，递推地执行该过程。最后使用辗转相除法进行化简。

代码

class Solution {
public:
    vector<int> fraction(vector<int>& cont) {
        vector<int> result;
        int n,m;//n为分子，m为分母
        int oldN,oldM;
        //首先以an-1为起点,初始化[n,m]
        n = cont.at(cont.size()-1);
        m = 1;

        //接下来循环处理an-2到a0
        for(int i= cont.size()-2;i >= 0;i--){
            oldN = n;
            oldM = m;
            n = cont.at(i) * oldN + oldM;
            m = oldN; 
        }


        //下面进行分式化简
        int a,b,c,d=1;
        a = n, b = m;
        while(a!=0){
            c = a/b;
            d = a - (b*c);
            if(d == 0)
                break;
            a = b;
            b = d;
        }
        if(a==0){
            result.push_back(0);
            result.push_back(1);
        }
        else{
            n = n/b;
            m = m/b;
            result.push_back(n);
            result.push_back(m);
        }
        return result;
    }
};