20200309_PID控制实现

最新推荐文章于 2023-04-20 20:52:13 发布

原创最新推荐文章于 2023-04-20 20:52:13 发布 · 560 阅读

14 ·

CC 4.0 BY-SA版权

技术日记专栏收录该内容

0 篇文章

订阅专栏

本文探讨了二维码导航AGV（自动导引车）控制系统的实现，详细讲解了PID控制算法在AGV定位和路径跟踪中的应用。通过C语言实现了位置型、增量型和积分分离型PID控制器，并讨论了抗积分饱和的PID控制策略。

二维码导航AGV控制系统研究

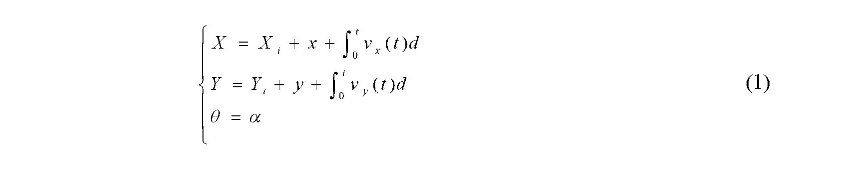
计算出二维码中心相对于图像坐标系原点的位置X1, Y1和二维码的L边线在坐标系中的倾角ɑ1, 经坐标变换后计算AGV相对于二维码的位姿P (x, y, α) [5], 其中x=-x1, y=-y1,。

右转运动方程在这里插入图片描述

PID的C语言实现

位置型PID的实现

/*偏差不为0，比例环节起作用
 * 积分环节用来消除静差，将积累误差加到原有系统上以抵消系统的静差。
 * ************************************
 * 微分环节，根据偏差信号的变化趋势来进行调节，增加系统的快速性
***********变量说明
 * 1.输入量为rin(t)
 * 2.输出量为rout(t)
 * 3.偏差量为err(t)=rin(t)-rout(t)
 * **连续公式u(x)=kp*err(t)+(1/T)*Ierr(t)dt+Td*derr(t)/dt
 ************离散化
 *假设采样间隔为T，在第KT时刻
 * err(K)=rin(K)-rout(K)
 * 积分环节的表达：（加和）err(K)+err(K+1)+...
 * 微分环节的表达：（斜率）[err(K)-err(K-1)]/T
 * (位置型) u(K)=kp*err(k)+ki*Eerr(K)+kd*(err(k)-err(k-1))
 */
#include<stdio.h>
#include<stdlib.h>
struct _pid
{
    float f_setSpeed;/*设定速度*/
    float f_actualSpeed;/*实际速度*/
    float f_err;/*偏差值*/
    float f_errLast;/*上一个偏差值*/
    float f_Kp,f_Ki,f_Kd;/*比例积分微分系数*/
    float voltage;/*执行器变量*/
    float integral;/*定义积分值*/
}pid;
void PID_init()
{
    pid.f_setSpeed=0.0;
    pid.f_actualSpeed==0.0;
    pid.f_err=0.0;
    pid.f_errLast=0.0;
    pid.voltage=0.0;
    pid.integral=0.0;
    pid.f_Kp=0.2;
    pid.f_Ki=0.015;
    pid.f_Kd=0.2;
}
float PID_realize(float speed)
{
    pid.f_setSpeed=speed;
    pid.f_err=pid.f_setSpeed-pid.f_actualSpeed;
    pid.integral+=pid.f_err;
    /*u(K)=kp*err(k)+ki*Eerr(K)+kd*(err(k)-err(k-1))*/
    pid.voltage=pid.f_Kp*pid.f_err+pid.f_Ki*pid.integral+pid.f_Kd*(pid.f_err-pid.f_errLast);
    pid.f_actualSpeed=pid.voltage;
    pid.f_errLast=pid.f_err;
    return pid.f_actualSpeed;
}
int main()
{
    PID_init();
    int cout=0;
    while(cout<1000)
    {
        float speed =PID_realize(200.0);
        printf("%4d,   %f\n",cout,speed);
        ++cout;
    }
    return 0;
}

 * ****在启动、结束或大幅度增减设定时，短时间内系统输出有很大的偏
 * 差，会造成PID运算的积分积累，导致控制量超过执行机构可能允许的最
 * 大动作范围，引起较大的超调，甚至是震荡。

增量型PID的实现

偏差不为0，比例环节起作用

积分环节用来消除静差，将积累误差加到原有系统上以抵消系统的静差
微分环节，根据偏差信号的变化趋势来进行调节，增加系统的快速性
***********变量说明
1.输入量为rin(t)
2.输出量为rout(t)
3.偏差量为err(t)=rin(t)-rout(t)
**连续公式u(x)=kp*err(t)+(1/T)Ierr(t)dt+Tdderr(t)/dt
************离散化
*假设采样间隔为T，在第KT时刻
err(K)=rin(K)-rout(K)
积分环节的表达：（加和）err(K)+err(K+1)+…
微分环节的表达：（斜率）[err(K)-err(K-1)]/T
(位置型) u(K)=kperr(k)+kiEerr(K)+kd*(err(k)-err(k-1))
(增量型)tri U(K)=kp*(err(K)-err(k-1))+kierr(K)+kd(err(K)-2*err(K-1)+err(K-2)）

/*偏差不为0，比例环节起作用
 * 积分环节用来消除静差，将积累误差加到原有系统上以抵消系统的静差
 * 微分环节，根据偏差信号的变化趋势来进行调节，增加系统的快速性
***********变量说明
 * 1.输入量为rin(t)
 * 2.输出量为rout(t)
 * 3.偏差量为err(t)=rin(t)-rout(t)
 * **连续公式u(x)=kp*err(t)+(1/T)*Ierr(t)dt+Td*derr(t)/dt
 ************离散化
 *假设采样间隔为T，在第KT时刻
 * err(K)=rin(K)-rout(K)
 * 积分环节的表达：（加和）err(K)+err(K+1)+...
 * 微分环节的表达：（斜率）[err(K)-err(K-1)]/T
 * (位置型) u(K)=kp*err(k)+ki*Eerr(K)+kd*(err(k)-err(k-1))
 * (增量型)tri U(K)=kp*(err(K)-err(k-1))+ki*err(K)+kd*(err(K)-2*err(K-1)+err(K-2))
*/
#include<stdio.h>
#include<stdlib.h>
/*定义变量*/
struct _pid
{
    float f_setSpeed;/*设定速度*/
    float f_actualSpeed;/*实际速度*/
    float f_err;/*偏差值*/
    float f_errLast;/*上一个偏差值*/
    float f_errLastL;/*上上一个偏差*/
    float f_Kp,f_Ki,f_Kd;/*比例积分微分系数*/
}pid;
/*初始化PID*/
void PID_init()
{
    pid.f_setSpeed=0.0;
    pid.f_actualSpeed==0.0;
    pid.f_err=0.0;
    pid.f_errLast=0.0;
    pid.f_errLastL=0.0;
    pid.f_Kp=0.2;
    pid.f_Ki=0.015;
    pid.f_Kd=0.2;
}
/*实现增量PID*/
float incrementalPID_realize(float speed)
{
    pid.f_setSpeed=speed;
    pid.f_err=pid.f_setSpeed-pid.f_actualSpeed;
    /*tri U(K)=kp*(err(K)-err(k-1))+ki*err(K)+kd*(err(K)-2*err(K-1)+err(K-2))*/
    float incrementalSpeed=pid.f_Kp*(pid.f_err-pid.f_errLast)+pid.f_Ki*pid.f_err+pid.f_Kd*(pid.f_err+pid.f_errLastL-2*pid.f_errLast);
    pid.f_actualSpeed+=incrementalSpeed;
    pid.f_errLastL=pid.f_errLast;
    pid.f_errLast=pid.f_err;
    return pid.f_actualSpeed;
}/*算法测试*/
int main()
{
    PID_init();
    int cout=0;
    while(cout<1022)
    {
        float speed =incrementalPID_realize(200.0);
        printf("%4d,   %f\n",cout,speed);
        ++cout;
    }
    return 0;
}

积分分离型PID的实现

/*偏差不为0，比例环节起作用
 * 积分环节用来消除静差，将积累误差加到原有系统上以抵消系统的静差。
 * ************************************
 * 微分环节，根据偏差信号的变化趋势来进行调节，增加系统的快速性
***********变量说明
 * 1.输入量为rin(t)
 * 2.输出量为rout(t)
 * 3.偏差量为err(t)=rin(t)-rout(t)
 * **连续公式u(x)=kp*err(t)+(1/T)*Ierr(t)dt+Td*derr(t)/dt
 ************离散化
 *假设采样间隔为T，在第KT时刻
 * err(K)=rin(K)-rout(K)
 * 积分环节的表达：（加和）err(K)+err(K+1)+...
 * 微分环节的表达：（斜率）[err(K)-err(K-1)]/T
 * (位置型) u(K)=kp*err(k)+ki*Eerr(K)+kd*(err(k)-err(k-1))
 */
#include<stdio.h>
#include<stdlib.h>
struct _pid
{
    float f_setSpeed;/*设定速度*/
    float f_actualSpeed;/*实际速度*/
    float f_err;/*偏差值*/
    float f_errLast;/*上一个偏差值*/
    float f_Kp,f_Ki,f_Kd;/*比例积分微分系数*/
    float voltage;/*执行器变量*/
    float integral;/*定义积分值*/
    float f_KpFlag;/*积分标志位*/
}pid;
void PID_init()
{
    pid.f_setSpeed=0.0;
    pid.f_actualSpeed==0.0;
    pid.f_err=0.0;
    pid.f_errLast=0.0;
    pid.voltage=0.0;
    pid.integral=0.0;
    pid.f_Kp=0.2;
    pid.f_Ki=0.015;
    pid.f_Kd=0.2;
    pid.f_KpFlag=0;
}
float PID_realize(float speed)
{
    pid.f_setSpeed=speed;
    pid.f_err=pid.f_setSpeed-pid.f_actualSpeed;
    if(abs(pid.f_err)>10)
    {
        pid.f_kpFlag=0;
    }
    else{
    pid.integral+=pid.f_err;    
    pid.f_kpFlag=0;
    }
    
    /*u(K)=kp*err(k)+ki*Eerr(K)+kd*(err(k)-err(k-1))*/
    pid.voltage=pid.f_Kp*pid.f_err+pid.f_Ki*pid.integral+pid.f_Kd*(pid.f_err-pid.f_errLast);
    pid.f_actualSpeed=pid.voltage;
    pid.f_errLast=pid.f_err;
    return pid.f_actualSpeed;
}
int main()
{
    PID_init();
    int cout=0;
    while(cout<1000)
    {
        float speed =PID_realize(200.0);
        printf("%4d,   %f\n",cout,speed);
        ++cout;
    }
    return 0;
}

/*偏差不为0，比例环节起作用
 * 积分环节用来消除静差，将积累误差加到原有系统上以抵消系统的静差。
 * ******************积分分离PID控制
 * 当被控量与设定值偏差较大时，取消积分作用，当被控量接近给定值时
 * ，引入积分控制，消除静差，提高精度。
 * ************************************
 * 微分环节，根据偏差信号的变化趋势来进行调节，增加系统的快速性
***********变量说明
 * 1.输入量为rin(t)
 * 2.输出量为rout(t)
 * 3.偏差量为err(t)=rin(t)-rout(t)
 * **连续公式u(x)=kp*err(t)+(1/T)*Ierr(t)dt+Td*derr(t)/dt
 ************离散化
 *假设采样间隔为T，在第KT时刻
 * err(K)=rin(K)-rout(K)
 * 积分环节的表达：（加和）err(K)+err(K+1)+...
 * 微分环节的表达：（斜率）[err(K)-err(K-1)]/T
 * (位置型) u(K)=kp*err(k)+ki*Eerr(K)+kd*(err(k)-err(k-1))
 * (增量型)trℹ U(K)=kp*(err(K)-err(k-1))+ki*err(K)+kd*(err(K)-2*err(K-1)+err(K-2))
*/
#include<stdio.h>
#include<stdlib.h>
const int Vl=2;
const int t=1;//
const int B=50;
struct _pid
{
    float f_set;/*设定速度*/
    float f_actual;/*实际速度*/
    float f_e;/*偏差值*/
    float f_eLast;/*上一个偏差值*/
    float f_Kp,f_Ki,f_Kd;/*比例积分微分系数*/
    float P;/*执行器变量*/
    float integral;/*定义积分值*/
    int int_KpFlag;
}ypid,qpid;
void PID_init()
{
    /*位置pid纠正初始化*/
    ypid.f_set=0.0;
    ypid.f_actual=0.0;
    ypid.f_e=0.0;
    ypid.f_eLast=0.0;
    ypid.P=1;
    ypid.integral=0.0;
    ypid.f_Kp=0.2;
    ypid.f_Ki=8;
    ypid.f_Kd=67;
    /*角度pid纠正初始化*/
    qpid.f_set=0.0;
    qpid.f_actual=0;
    qpid.f_e=0;
    qpid.f_eLast=0.0;
    qpid.P=1;
    qpid.integral=0.0;
    qpid.f_Kp=28.9;
    qpid.f_Ki=89;
    qpid.f_Kd=1;
}
void YPID_realize(float postion,float en,float angle,float aen)
{
    ypid.f_actual=postion;
    ypid.f_e=postion;
    qpid.f_actual=angle;
    qpid.f_e=angle;
    int cout=0;
    while((abs(ypid.f_e)>en*0.2||abs(qpid.f_e)>aen*0.2)&&cout<1000)
    {
       float Vc=(1+(ypid.P-1)/2)*Vl;//中心速度
       float v=(1-ypid.P)*Vl;//差速
    //ypid.f_e=ypid.f_e+(2*(abs(1-ypid.P)*Vl*t))/B;
       qpid.f_e=qpid.f_e+2*v*t/B;
       ypid.f_e=ypid.f_e+Vc*1*t+Vc*v*t*t/B;//纠正之后的误差
           /*位移的分离积分PID*/
    if(abs(ypid.f_e)>=en*1)
    {
        ypid.int_KpFlag=0;
    }
    else
    {
         ypid.integral+=ypid.f_e;
         if(abs(ypid.f_e)<en&&abs(ypid.f_e)>=en*0.5)
         {
             ypid.int_KpFlag=0.2;
         }
         else if(abs(ypid.f_e)<en*0.5&&abs(ypid.f_e)>=en*0.3){
             ypid.int_KpFlag=0.5;
         }
         else
         {
             ypid.int_KpFlag=1;
         }
    }
    /*u(K)=kp*err(k)+ki*Eerr(K)+kd*(err(k)-err(k-1))*/
    ypid.P=ypid.f_Kp*ypid.f_e+ypid.int_KpFlag*ypid.f_Ki*ypid.integral+ypid.f_Kd*(ypid.f_e-ypid.f_eLast);
    /******/
    /**角度的积分分离的PID*/
    if(abs(qpid.f_e)>=aen*1)
    {
        qpid.int_KpFlag=0;
    }
    else
    {
         qpid.integral+=qpid.f_e;
         if(abs(qpid.f_e)<aen&&abs(qpid.f_e)>=aen*0.5)
         {
             qpid.int_KpFlag=0.2;
         }
         else if(abs(qpid.f_e)<aen*0.5&&abs(qpid.f_e)>=aen*0.3){
             qpid.int_KpFlag=0.5;
         }
         else
         {
             qpid.int_KpFlag=1;
         }
    }
    /*u(K)=kp*err(k)+ki*Eerr(K)+kd*(err(k)-err(k-1))*/
    qpid.P=qpid.f_Kp*qpid.f_e+qpid.int_KpFlag*qpid.f_Ki*qpid.integral+qpid.f_Kd*(qpid.f_e-qpid.f_eLast);
    qpid.P=abs(qpid.P)>3?3:qpid.P;
    ypid.P=abs(ypid.P)>3?3:qpid.P;
    /****/
    ypid.f_eLast=ypid.f_e;
    qpid.f_eLast=qpid.f_e;
    printf("%4d, en=%0.2f,aen=%0.1f,yP=%5.2f qP=%5.2f ye=%0.2f qe=%0.2f\n",cout++,en,aen,ypid.P,qpid.P,ypid.f_e,qpid.f_e);
    }
}
int main()
{
    PID_init();
    YPID_realize(10,1,60,2);
    return 0;
}

抗积分饱和的PID控制算法

由于积分作用不断累加，导致执行机构达到极限位置，执行器开度不可能再增大。出现反向偏差，从饱和区退出。进入饱和区越深退出饱和区时间越长。在这段时间内执行机构停留在极限位置不随偏差反向做出改变，系统像失控般，造成控制性能恶化。

方法：在计算u(k)时，判断上一时刻的控制量u(k-1)是否超出极限范围：如果>max,只累加负偏差；如果<min，只累加正偏差，避免长期停留在饱和区。

/*偏差不为0，比例环节起作用
 * 积分环节用来消除静差，将积累误差加到原有系统上以抵消系统的静差。
 * ************************************
 * 微分环节，根据偏差信号的变化趋势来进行调节，增加系统的快速性
***********变量说明
 * 1.输入量为rin(t)
 * 2.输出量为rout(t)
 * 3.偏差量为err(t)=rin(t)-rout(t)
 * **连续公式u(x)=kp*err(t)+(1/T)*Ierr(t)dt+Td*derr(t)/dt
 ************离散化
 *假设采样间隔为T，在第KT时刻
 * err(K)=rin(K)-rout(K)
 * 积分环节的表达：（加和）err(K)+err(K+1)+...
 * 微分环节的表达：（斜率）[err(K)-err(K-1)]/T
 * (位置型) u(K)=kp*err(k)+ki*Eerr(K)+kd*(err(k)-err(k-1))
 */
#include<stdio.h>
#include<stdlib.h>
struct _pid
{
    float f_setSpeed;/*设定速度*/
    float f_actualSpeed;/*实际速度*/
    float f_err;/*偏差值*/
    float f_errLast;/*上一个偏差值*/
    float f_Kp,f_Ki,f_Kd;/*比例积分微分系数*/
    float voltage;/*执行器变量*/
    float integral;/*定义积分值*/
    float umax;/*极大值*/
    float umin;/*极小值*/
}pid;
void PID_init()
{
    pid.f_setSpeed=0.0;
    pid.f_actualSpeed==0.0;
    pid.f_err=0.0;
    pid.f_errLast=0.0;
    pid.voltage=0.0;
    pid.integral=0.0;
    pid.f_Kp=0.2;
    pid.f_Ki=0.015;
    pid.f_Kd=0.2;
    pid.umax=400;
    pid.umin=-200;
}
float PID_realize(float speed)
{int index;
    pid.f_setSpeed=speed;
    pid.f_err=pid.f_setSpeed-pid.f_actualSpeed;
 if(pid.f_actualSpeed>pid.umax)
 {
    if(abs(pid.f_err)>10)
    {
        index=0;
    }
    else{    
    index=1;
        if(pid.err<0)
        {
            pid.integral+=pid.err
        }
    }
     
 }
 else if(pid.f_actualSpeed<pid.umin)
 {
     
    if(abs(pid.f_err)>10)
    {
        index=0;
    }
    else{    
    index=1;
        if(pid.err>0)
        {
            pid.integral+=pid.err
        }
    }
 }
    
    /*u(K)=kp*err(k)+ki*Eerr(K)+kd*(err(k)-err(k-1))*/
    pid.voltage=pid.f_Kp*pid.f_err+index*pid.f_Ki*pid.integral+pid.f_Kd*(pid.f_err-pid.f_errLast);
    pid.f_actualSpeed=pid.voltage;
    pid.f_errLast=pid.f_err;
    return pid.f_actualSpeed;
}
int main()
{
    PID_init();
    int cout=0;
    while(cout<1000)
    {
        float speed =PID_realize(200.0);
        printf("%4d,   %f\n",cout,speed);
        ++cout;
    }
    return 0;
}

r
}
}
}

/*u(K)=kp*err(k)+ki*Eerr(K)+kd*(err(k)-err(k-1))*/
pid.voltage=pid.f_Kp*pid.f_err+index*pid.f_Ki*pid.integral+pid.f_Kd*(pid.f_err-pid.f_errLast);
pid.f_actualSpeed=pid.voltage;
pid.f_errLast=pid.f_err;
return pid.f_actualSpeed;

}
int main()
{
PID_init();
int cout=0;
while(cout<1000)
{
float speed =PID_realize(200.0);
printf("%4d, %f\n",cout,speed);
++cout;
}
return 0;
}