一、算法原理
(1)基本算法
决策树(Decision Tree),基于“树”结构进行决策:
每个内部结点对应一个属性测试;
每个分支对应属性测试的一种可能取值;
每个叶结点对应一个决策结果。

学习过程:通过对训练样本的分析来确定“划分属性”(即内部结点所对应的属性)。
预测过程:将测试示例从根结点开始,沿着划分属性所构成的“判定测试序列”下行,直到叶结点。
策略:分而治之(Divide-and-Conquer)
自根至叶递归;
在每个内部结点寻找一个划分(或测试)属性。
递归停止条件:
当前结点包含的样本全属于同一类别,无需划分;
当前属性集为空, 或是所有样本在所有属性上取值相同,无法划分;
当前结点包含的样本集合为空,不能划分。

(2)划分
①信息增益
信息熵(Entropy):度量样本集合“纯度”最常用的一种指标。
假定当前样本集合D中第k类样本(k=1, 2, …, |y|)所占的比例为![]() ,则D的信息熵定义为:
,则D的信息熵定义为:

Ent(D)的值越小,则D的纯度越高:
Ent(D)的最小值:0,此时D中只有一类;
最大值![]() ,此时D中每个样本都是一类。
,此时D中每个样本都是一类。
信息增益(Information Gain):划分带来纯度的提升,信息熵的下降。
离散属性a的取值:![]()
![]() :D中在a上取值等于
:D中在a上取值等于![]() 的样本集合
的样本集合
以属性a对数据集D进行划分所获得的信息增益为:

信息增益越大,意味着使用属性a来进行划分所获得的“纯度提升”越大。
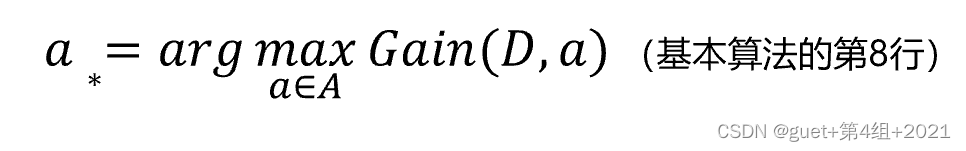
ID3决策树算法:在候选属性集合中选取信息增益最高的属性。
举例:西瓜数据集(后面以该数据集为例)
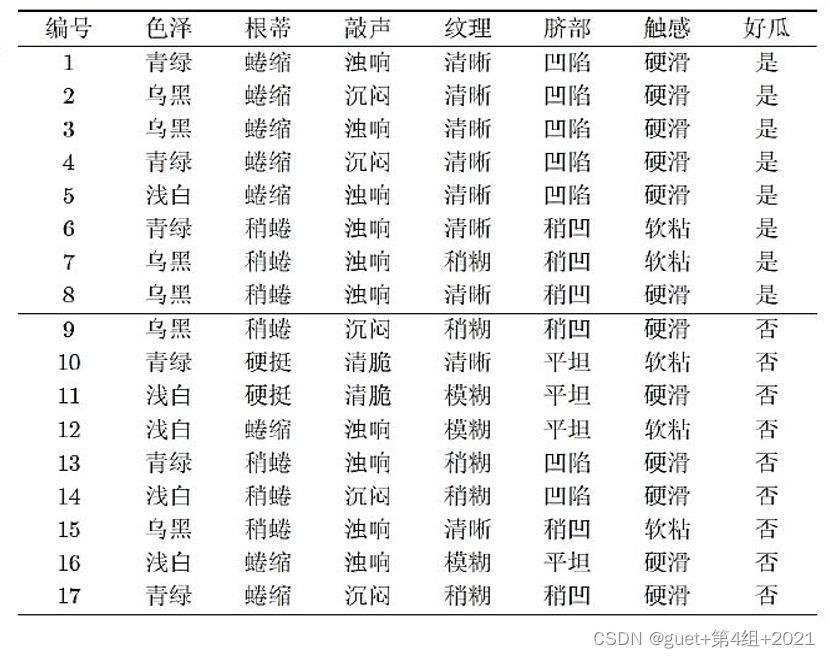
计算根结点的信息熵Ent(D):
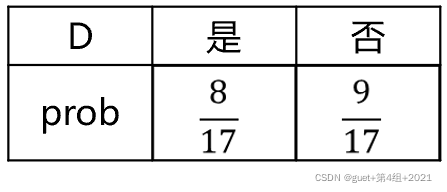
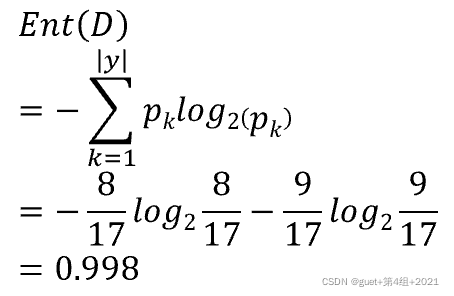
当前属性集合A={色泽,根蒂,敲声,纹理,脐部,触感}
以属性“色泽”为例,其对应的3个数据子集为:
![]() (色泽=青绿),
(色泽=青绿),![]() (色泽=乌黑),
(色泽=乌黑),![]() (色泽=浅白)
(色泽=浅白)
以子集![]() 为例,其包含6个样例,{1,4,6,10,13,17},占总样例数的6/17,其中正例占
为例,其包含6个样例,{1,4,6,10,13,17},占总样例数的6/17,其中正例占![]() 样例数p1=3/6,反例占D1样例数p2=3/6 ,因此
样例数p1=3/6,反例占D1样例数p2=3/6 ,因此
![]()
同理,
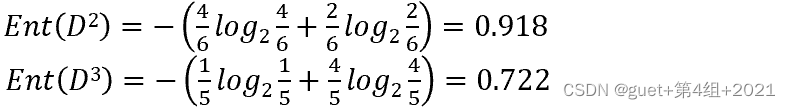
属性“色泽”的信息增益为:
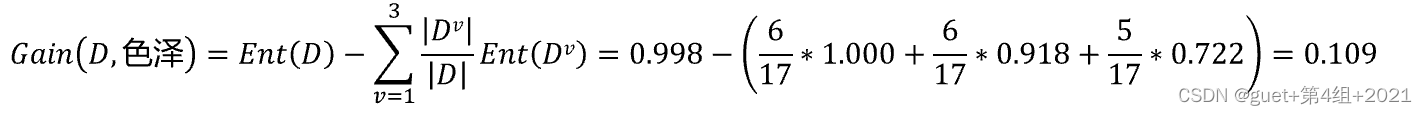
全部属性的信息增益为:

属性“纹理”的信息增益最大,被选为划分属性
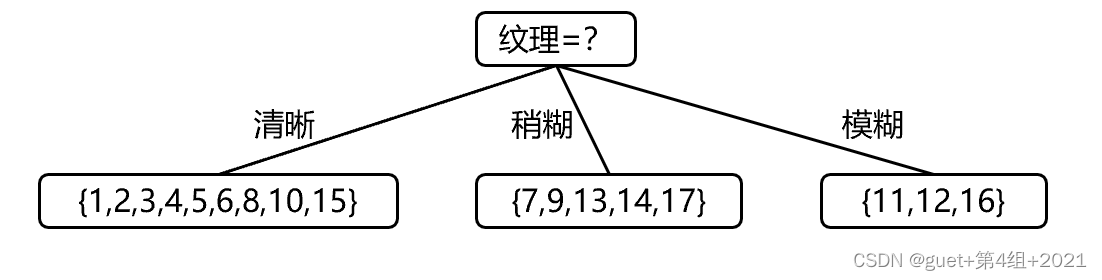
对每个分支结点根据信息增益准则做进一步划分,得到决策树:

信息增益准则对可取值数目较多的属性有所偏好。
②增益率
增益率(Gain Ratio):
![]()
属性a的固有值(Intrinsic Value):
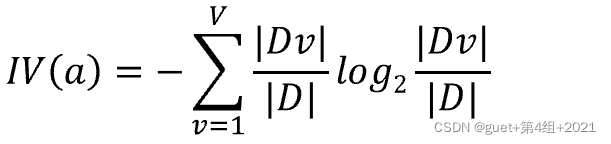
属性a的可能取值数目越多,即 V 越大,则IV(a)的值通常就越大。
增益率准则对可取值数目较少的属性有所偏好。
C4.5决策树算法:从候选属性集合中找出信息增益高于平均水平的,再从中选取增益率最高的。
③基尼指数
基尼值(Gini):度量数据集D的纯度
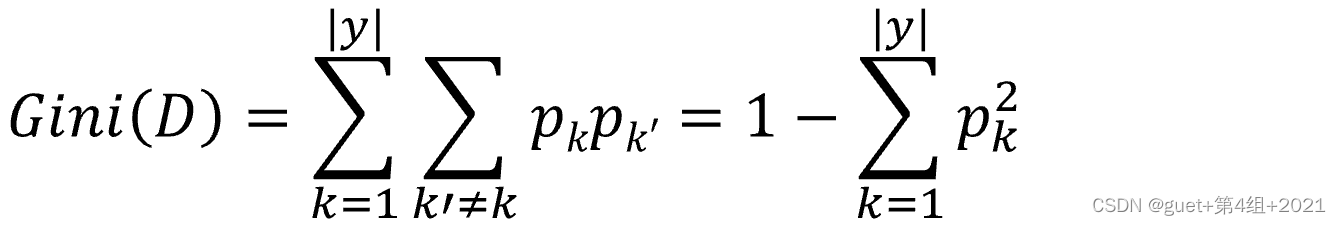
反映了从D中随机抽取两个样例,其类别标记不一致的概率。
Gini(D)越小,数据集D的纯度越高。
属性a的基尼指数(Gini Index):
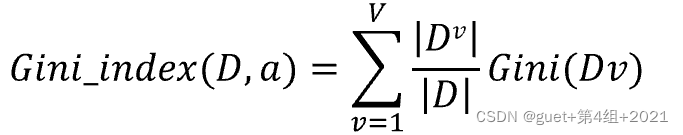
CART决策树算法:在候选属性集合中选取使划分后基尼指数最小的属性。
![]()
总结

(3)剪枝
为了尽可能正确分类训练样本,有可能造成分支过多,从而导致过拟合。
剪枝(Pruning):是决策树预防过拟合的主要手段,可通过主动去掉一些分支来降低过拟合的风险。
划分:划分选择对决策树的尺寸有较大影响,但对泛化性能的影响很有限。
剪枝:剪枝方法和程度对决策树泛化性能的影响更为显著。
剪枝的两种策略:
预剪枝(Pre-pruning):提前终止某些分支的生长(自上而下)。
后剪枝(Post-pruning):生成一棵完全树,再回头剪枝(自下而上)。
举例:
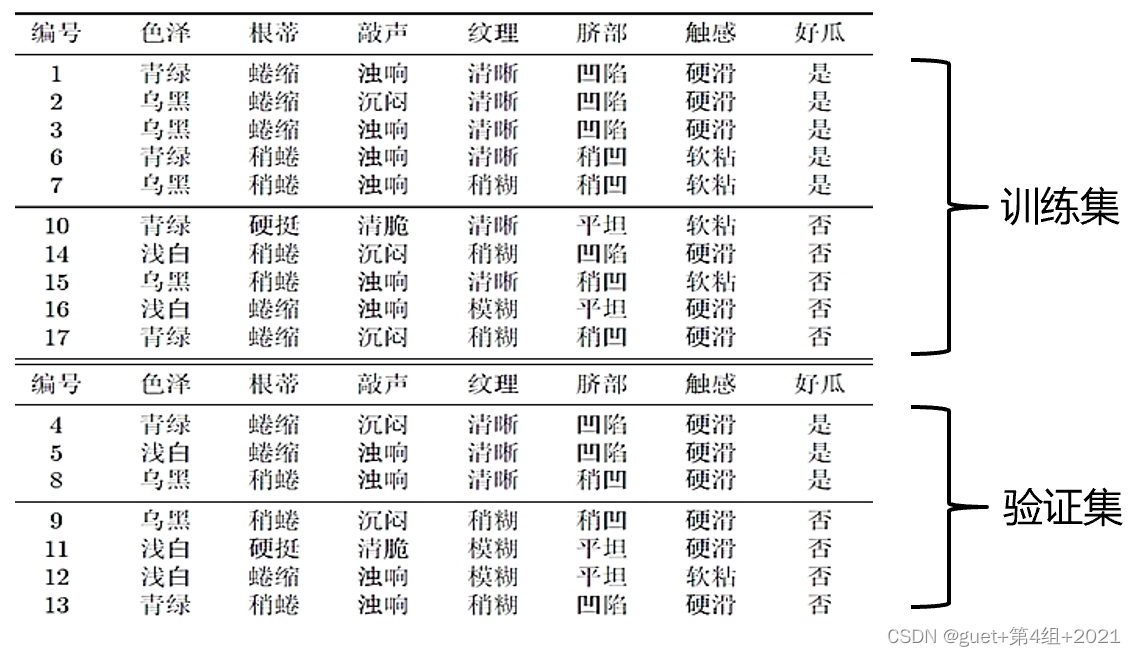
根据信息增益准则将训练集生成未剪枝决策树:
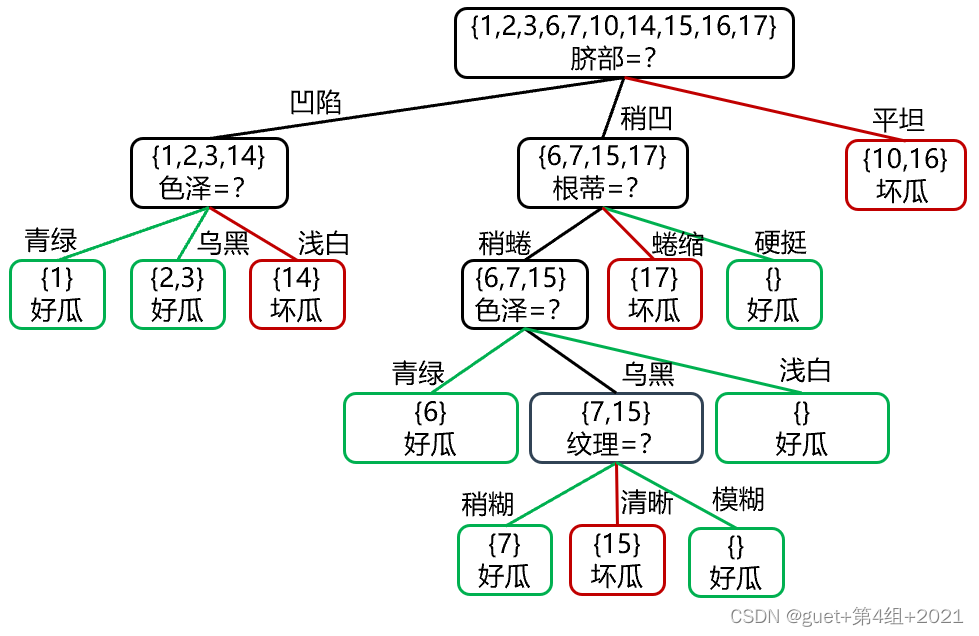
①预剪枝

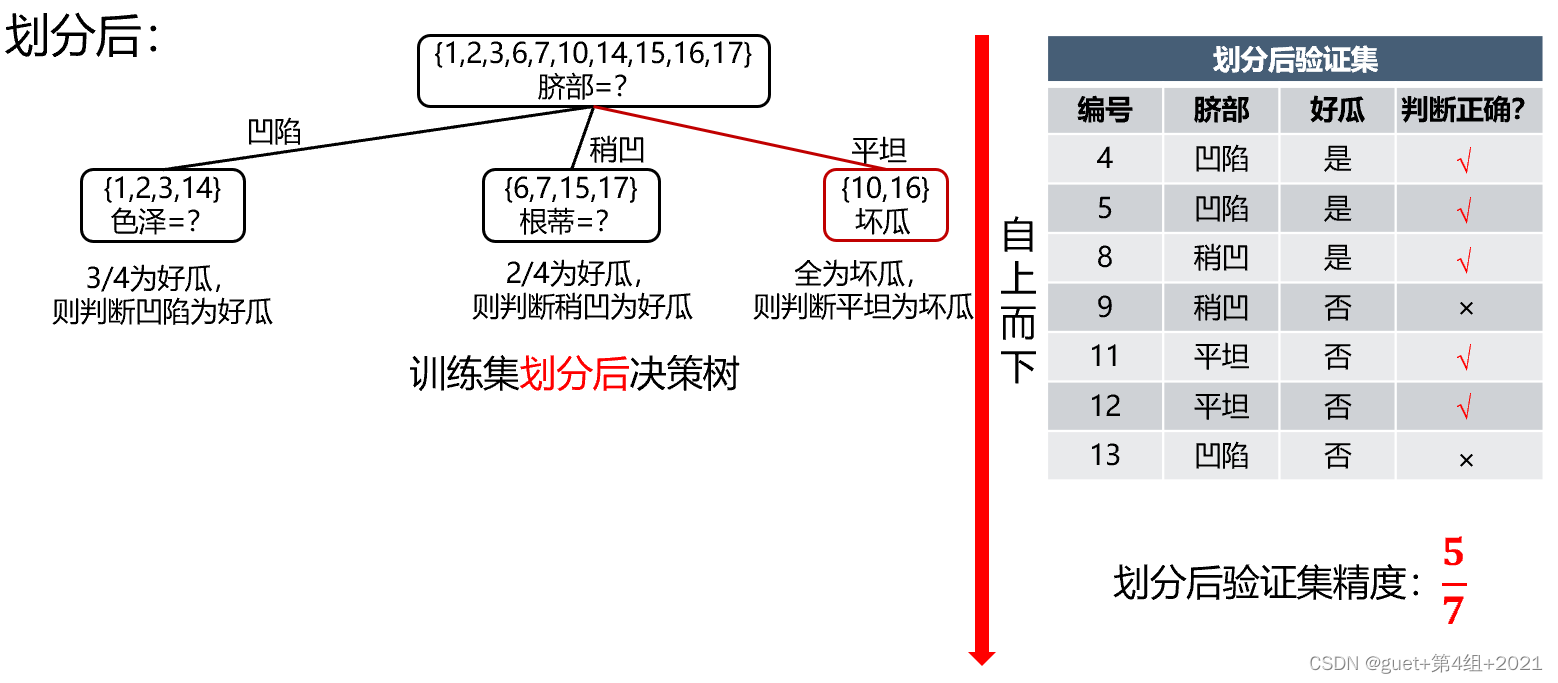
预剪枝决策判断:
划分前验证集精度:3/7 > 划分后验证集精度:5/7
划分后精度提高,保留划分;
精度降低或不变,禁止划分。
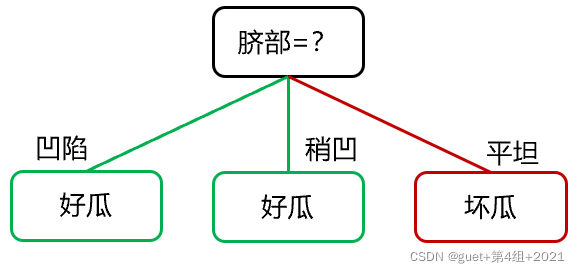
②后剪枝
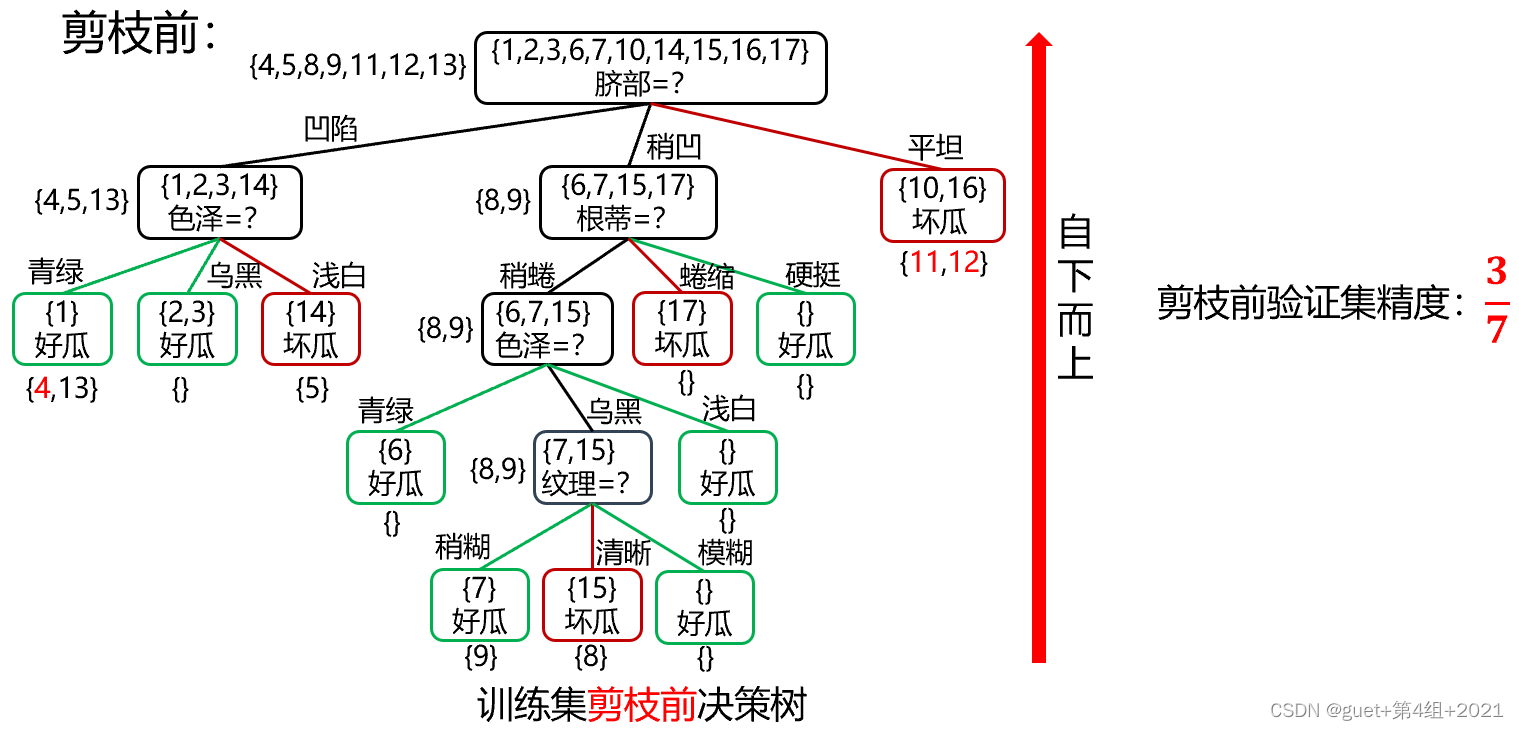
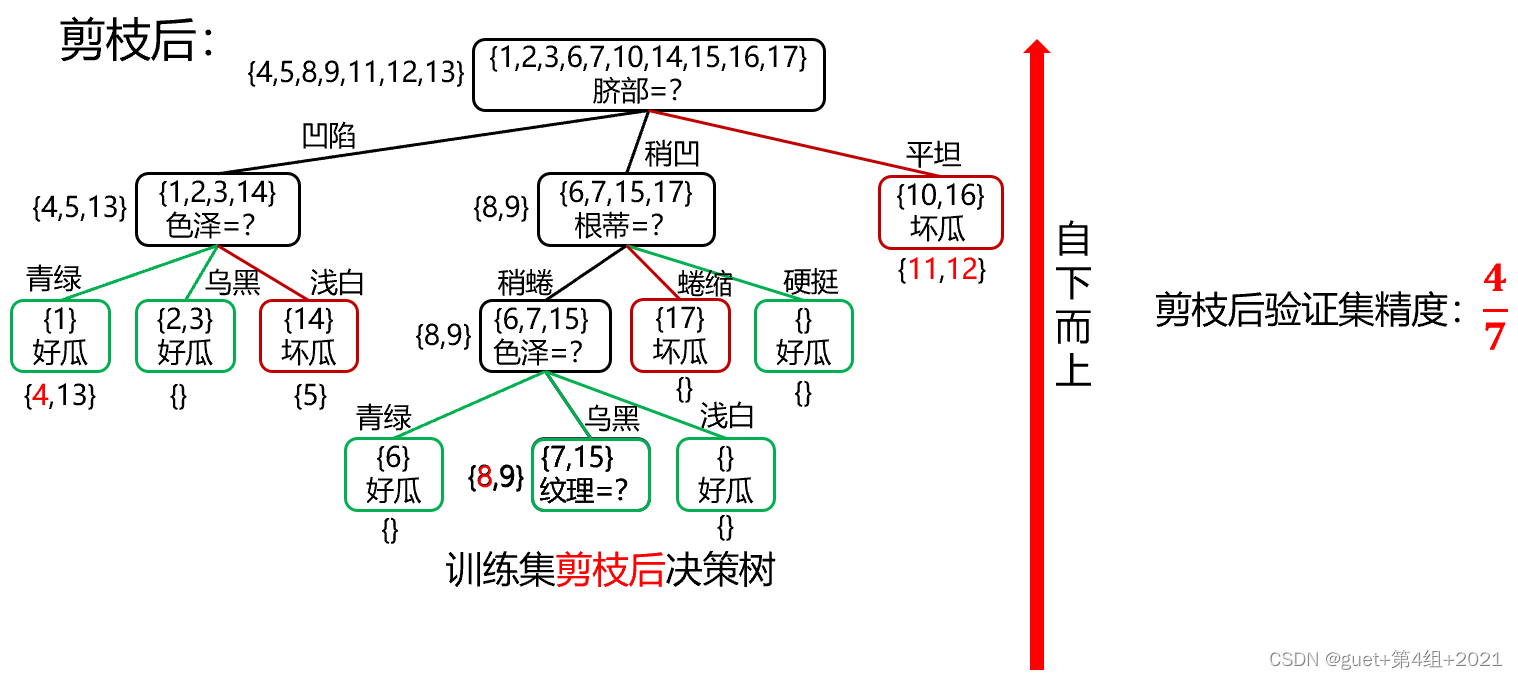
后剪枝决策判断:
剪枝前验证集精度:3/7 < 剪枝后验证集精度:4/7
剪枝后精度提高,进行剪枝;
精度降低或不变,不剪枝。
(奥卡姆剃刀准则(Occam’s Razor):如无必要,勿增实体。Entities should not be multiplied unnecessarily.)
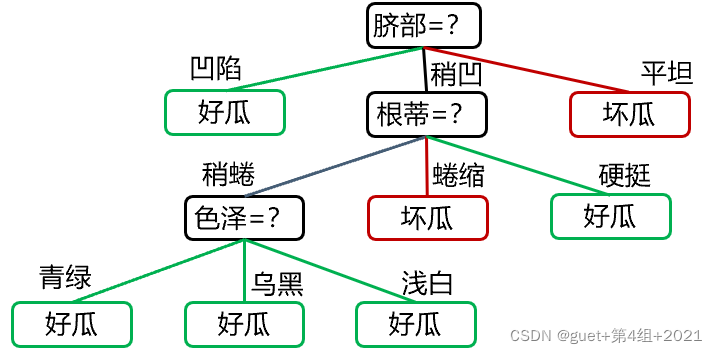
总结

二、算法实验
(1)任务
泰坦尼克乘客生存预测。
(2)步骤
①问题描述
泰坦尼克海难是著名的十大灾难之一,究竟多少人遇难,各方统计的结果不一。
数据集:
train.csv:训练数据集,包含特征信息和存活与否的标签。
test.csv:测试数据集,只包含特征信息。
训练集字段:
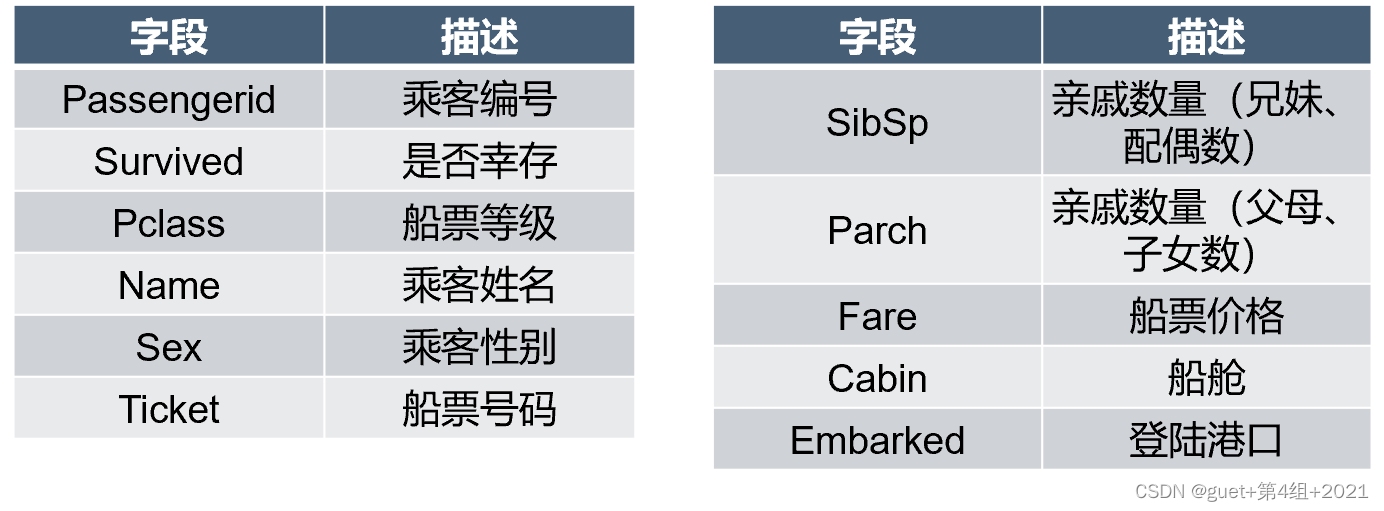
②准备过程
- 数据探索:
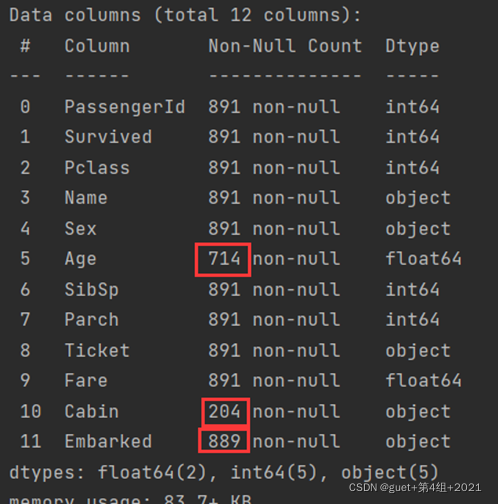
1、了解数据表的基本情况:行数、列数、每列的数据类型、数据完整度。
2、了解数据表的统计情况:总数、平均值、标准差、最小值、最大值等。
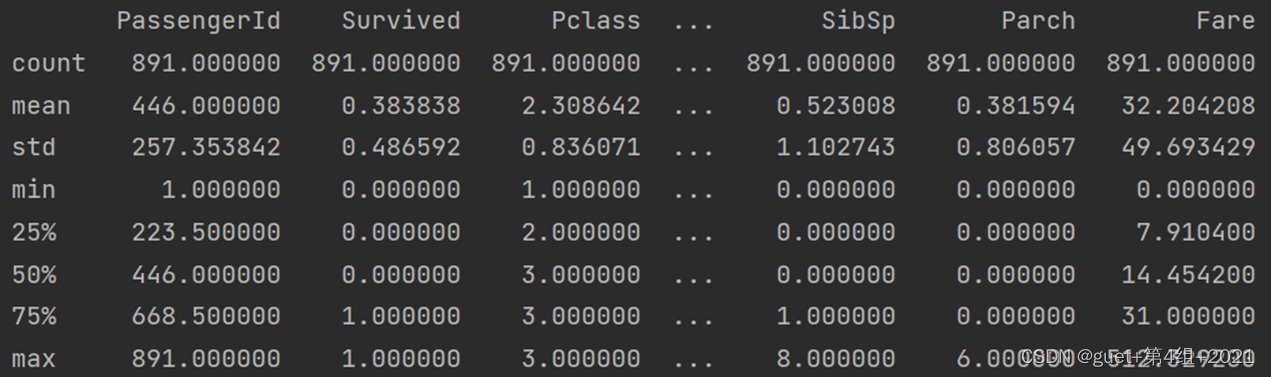
3、查看字符串类型(非数字)的整体情况。
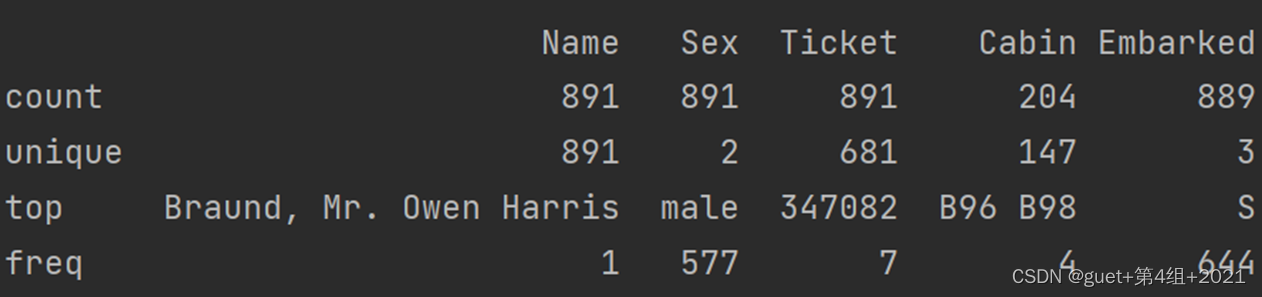
- 数据清洗:
1、Age、Embarked和 Cabin 这三个字段的数据有所缺失。
2、Age 为年龄字段,是数值型,通过平均值进行补齐。
3、Cabin 为船舱,有大量的缺失值,无法补齐。
4、Embarked 为登陆港口,有少量的缺失值。将其余缺失的 Embarked 数值均设置为 S(一共3个登陆港口,S港人数最多)。
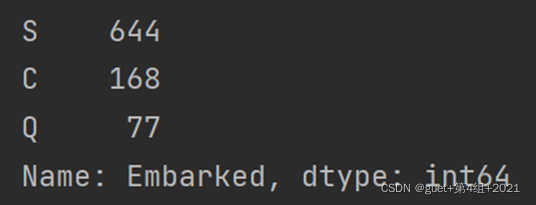
- 特征选择
1、PassengerId、Name对分类没有作用,放弃。
2、Cabin 字段缺失值太多,放弃。
3、Ticket 字段为船票号码,杂乱无章且无规律,放弃。
4、其余的字段包括:Pclass、Sex、Age、SibSp、Parch 和 Fare,可能会与乘客的生存预测分类有关系。
5、将特征值中为字符串的转成数值类型。如:sex用0,1表示。
![]()
- 生成决策树
1、使用sklearn生成决策树模型并训练。
2、criterion=‘entropy’意为基于信息熵标准建立决策树。
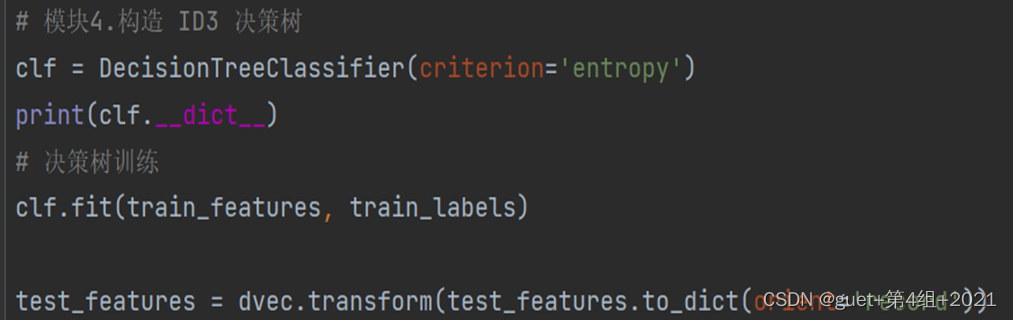
③模型预测及评估
- 决策树模型
1、由于没有测试集的实际结果,因此无法用测试集的预测结果与实际结果相对比。
2、使用K折交叉验证的方式,用大部分样本进行训练,少量的用于分类器的验证。
3、运行结果:
![]()
- 总结
1、特征选择是分类模型好坏的关键。选择什么样的特征,以及对应的特征值矩阵,决定了分类模型的好坏。通常情况下,特征值不都是数值类型,可以使用 DictVectorizer 类进行转化。
2、模型准确率需要考虑是否有测试集的实际结果可以做对比,当测试集没有真实结果可以对比时,需要使用 K 折交叉验证。





















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








