矩阵快速幂

最新推荐文章于 2025-06-01 00:01:08 发布

原创最新推荐文章于 2025-06-01 00:01:08 发布 · 243 阅读

0 ·

CC 4.0 BY-SA版权

算法同时被 3 个专栏收录

27 篇文章

订阅专栏

二分快速幂

3 篇文章

订阅专栏

矩阵二分快速幂优化dp

2 篇文章

订阅专栏

本文介绍了一种利用矩阵快速幂方法高效计算斐波那契数列第n项模m值的方法，适用于n最大可达10^18的情况。通过定义特定的矩阵形式并采用快速幂技巧，避免了传统递归方法的时间复杂度过高的问题。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

f(1)=1, f(2)=1 , f(n)=a*f(n-1)+b*f(n-2)，输出n和m，求 f(n) % m 的值。n是1到10^18次方的数。

如果按照朴素计算的话，由于18次方，还是特别慢。

如果使用矩阵形如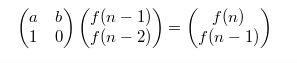，dp[n]=An−1⋅dp[1]

则f(n) :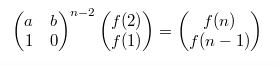

struct matrix{
    long long ab[k][k];
};

matrix mul(matrix a,matrix b){//两个矩阵相乘
    matrix c;

    for(int i = 0;i < k;i ++){
        for(int j = 0;j < k;j ++){
        c.ab[i][j] = 0;
        for(int l = 0;l < k;l ++){
            c.ab[i][j] += a.ab[i][l] * b.ab[l][j] % mod;
            c.ab[i][j] %= mod;
        }
    }
}
    return c;
}

matrix unit(){//单位矩阵
    matrix ras;

    for(int i = 0;i < k;i ++){
        for(int j = 0;j < k;j ++){
            if(i == j){
                ras.ab[i][j] = 1;
            }else{
                ras.ab[i][j] = 0;
            }
        }
    }
    return ras;
}

matrix pow(matrix A,long long n){/矩阵二分快速幂
    matrix ras = unit();
    matrix temp = A;
    for(;n;n/=2){
        if(n&1){
            ras = mul(ras,temp);
        }
        temp = mul(temp,temp);
    }
    return ras;
}