牛客ACM-[NOIP2002]过河卒

原创已于 2022-08-28 23:06:05 修改 · 259 阅读

5 ·

CC 4.0 BY-SA版权

文章标签：

#算法

于 2022-08-28 23:03:49 首次发布

牛客-dp 专栏收录该内容

5 篇文章

订阅专栏

本文介绍了一个经典的算法问题——过河卒问题，通过动态规划求解在存在障碍的情况下从起点到终点的不同路径数量。文章详细阐述了问题背景、解题思路及实现代码。

[NOIP2002]过河卒

题目描述

如图，A 点有一个过河卒，需要走到目标 B 点。卒行走规则：可以向下、或者向右。同时在棋盘上的任一点有一个对方的马（如上图的C点），该马所在的点和所有跳跃一步可达的点称为对方马的控制点。例如上图 C 点上的马可以控制 9 个点（图中的P1，P2 … P8 和 C）。卒不能通过对方马的控制点。
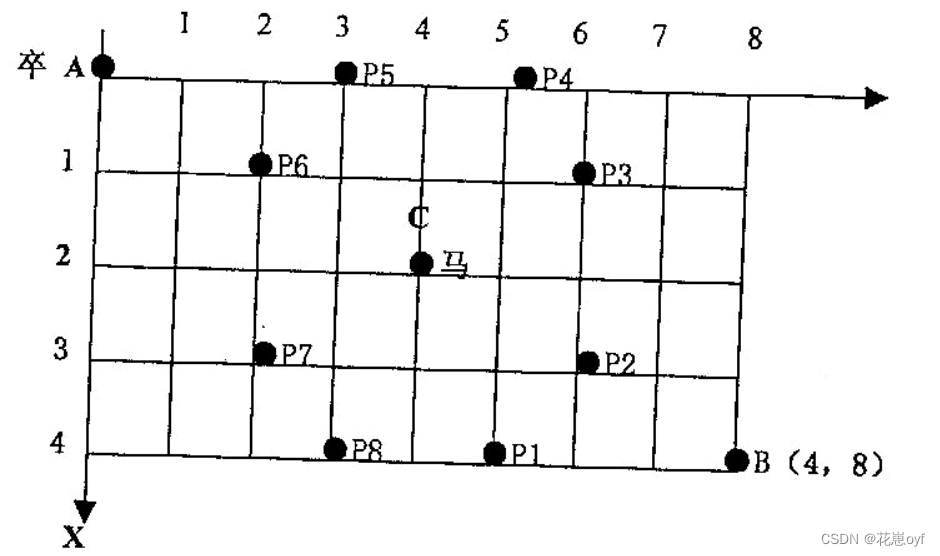
在这里插入图片描述
棋盘用坐标表示，A 点（0,0）、B 点（n,m）(n,m 为不超过 20 的整数，并由键盘输入)，同样马的位置坐标是需要给出的（约定: C<>A，同时C<>B）。现在要求你计算出卒从 A 点能够到达 B 点的路径的条数。

输入描述

输入B点的坐标（n,m）以及对方马的坐标（X,Y）{不用判错}

输出描述

输出一个整数（路径的条数）。

示例1

输入

6 6 3 2

输出

17

解题思路

把所有输入的坐标信息都自增一
用 dp[i][j] 表示从 (1,1) 走到 (i,j) 的方案数
先初始化马的控制点，用 ma[i][j]=1 表示
转台转移方程 dp[i][j]=dp[i-1][j]+dp[i][j-1]
注意 dp 数组要开 long long

代码

#include<iostream>
using namespace std;
typedef long long ll;
const int N=1e3+7;

int n,m,X,Y;
int ma[N][N];
ll dp[N][N];
int dx[]={-2,-2,-1,-1,1,1,2,2},dy[]={1,-1,2,-2,2,-2,1,-1};

void init(int x,int y){
    ma[x][y]=1;
    for(int i=0;i<8;i++){
        int xx=x+dx[i];
        int yy=y+dy[i];
        if(xx>=1&&yy>=1)
            ma[xx][yy]=1;
    }
}
int main(){
    ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
    cin>>n>>m>>X>>Y;
    init(X+1,Y+1);
    dp[1][1]=1;
    for(int i=1;i<=n+1;i++)
        for(int j=1;j<=m+1;j++){
            if(i==j&&i==1)continue;
            if(ma[i][j]==0)
                dp[i][j]=dp[i-1][j]+dp[i][j-1];
        }
    cout<<dp[n+1][m+1]<<endl;
    return 0;
}