[排序算法]选择排序

选择排序(Selection Sort)的基本思想是：首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。

第一个位置放最小的值(在未排序的范围选择)，第二个位置也放最小的值(在未排序的范围选择)，...，第n个位置也放最小的值。
排序过程：（默认升序）

1. 从原序列中找到最小值，与数组第一个元素交换；
2. 除第一个元素外，从剩下未排序的序列中找到最小值，与数组第二个元素交换；
3. 共N-1趟，每趟都找到未排序的最小值，放到已排序的序列后面。

唯一的好处可能就是不占用额外的内存空间了吧。
常用的选择排序方法有直接选择排序和堆排序。

#include <iostream>
#include <time.h>
#include <stdlib.h>
using namespace std;
void SelectSort(int* b,int len)
{
    for(int i=0;i<len-1;i++)
    {
        int minIndex = i;
        for(int j=i+1;j<len;j++)
        {
            if(b[minIndex]>b[j])
                minIndex=j;//记录最小值位置
        }
        if(minIndex != i)
        {
            int temp=b[minIndex];
            b[minIndex] = b[i];
            b[i] = temp;
        }
    }
}
int main()
{
    int a[10];
    srand(time(NULL));
    for (int i=0;i<10;i++)
    {
        a[i]=rand()%499+1;
    }
    cout<<"before sort numbers: ";
    for (int i=0;i<10;i++)
    {
        cout<<" "<<a[i];
    }
    cout<<endl;
    SelectSort(a,10);
    cout<<" after sort numbers: ";
    for (int i=0;i<10;i++)
    {
        cout<<" "<<a[i];
    }
    cout<<endl;
    return 0;
}

选择排序法的第一层循环从起始元素开始选到倒数第二个元素,主要是在每次进入的第二层循环之前,将外层循环的下标赋值给临时变量,接下来的第二层循环中,如果发现有比这个最小位置处的元素更小的元素,则将那个更小的元素的下标赋给临时变量,最后,在二层循环退出后,如果临时变量改变,则说明,有比当前外层循环位置更小的元素,需要将这两个元素交换.  

算法分析

其实选择排序是非常简单的，和冒泡排序有异曲同工之妙。就是把元素分成两部分，一部分是有序的，另外一部分是无序的；每次循环从无序的元素中选取一个元素放到有序的元素中，依次循环到最后把所有元素都放到了有序那一部分中；基本思路：

1. 外循环：循环每个位置（其实就是选择了这个位置，然后用内循环去选择一个合适的数，放到这个位置）；
2. 内循环：在无序元素中选择一个合适的数；
3. 把第二步选中的数据放到第一步选中的位置上就可以了；

 时间/空间复杂度

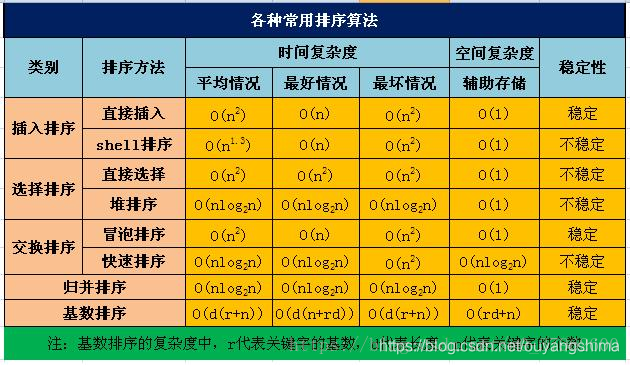
时间复杂度
可以很直观的看出选择排序的时间复杂度：就是两个循环消耗的时间；
比较时间：T = （n-1)）+ （n -2）+（n - 3）.... + 1; ?===>> ?T = ?[n*(n-1) ] / 2；
交换时间：最好的情况全部元素已经有序，则交换次数为0；最差的情况，全部元素逆序，就要交换 n-1 次；
所以最优的时间复杂度和最差的时间复杂度和平均时间复杂度都为 ：O(n^2)

空间复杂度
空间复杂度，最优的情况下（已经有顺序）复杂度为：O(0) ；最差的情况下（全部元素都要重新排序）复杂度为：O(n );；平均的时间复杂度：O(1)

稳定性

选择排序是给每个位置选择当前元素最小的，比如给第一个位置选择最小的，在剩余元素里面给第二个元素选择第二小的，依次类推，直到第n-1个元素，第n个元素不用选择了，因为只剩下它一个最大的元素了。那么，在一趟选择，如果一个元素比当前元素小，而该小的元素又出现在一个和当前元素相等的元素后面，那么交换后稳定性就被破坏了。比较拗口，举个例子，序列5 8 5 2 9，我们知道第一遍选择第1个元素5会和2交换，那么原序列中两个5的相对前后顺序就被破坏了，所以选择排序是一个不稳定的排序算法