拓扑排序-优快云博客

本文深入解析拓扑排序的概念，特别针对有向无环图（DAG），并详细阐述其算法流程，通过实例演示如何确定课程的正确学习顺序，同时提供Python实现代码。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

1. introduction

拓扑排序（Topological Sort）并不是一个纯粹的排序算法，它只是针对某一类图，找到一个可以执行的线性顺序

2. 有向无环图DAG

拓扑排序只是针对特定的一类图，那么是针对哪类图的呢？
答：Directed acyclic graph (DAG)，有向无环图。即：

这个图的边必须是有方向的；
图内无环

下图左边不是环，右边是
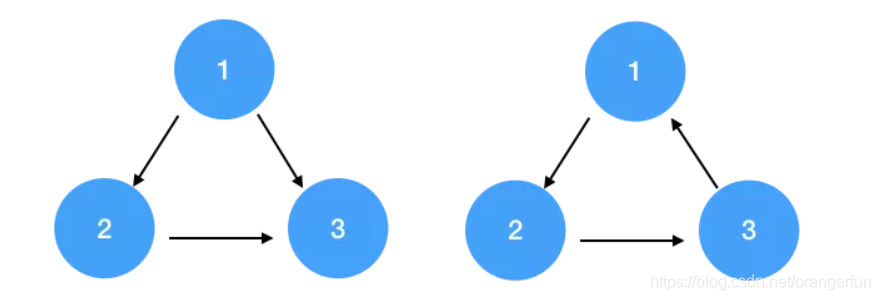
在这里插入图片描述
如果一个图里有环，比如右图，想执行1就要先执行3，想执行3就要先执行2，想执行2就要先执行1，这成了个死循环，无法找到正确的打开方式，所以找不到它的一个拓扑序

总结

如果这个图不是 DAG，那么它是没有拓扑序的；
如果是 DAG，那么它至少有一个拓扑序；
反之，如果它存在一个拓扑序，那么这个图必定是 DGA.

3. 拓扑排序

借用百度百科的这个课程表来说明
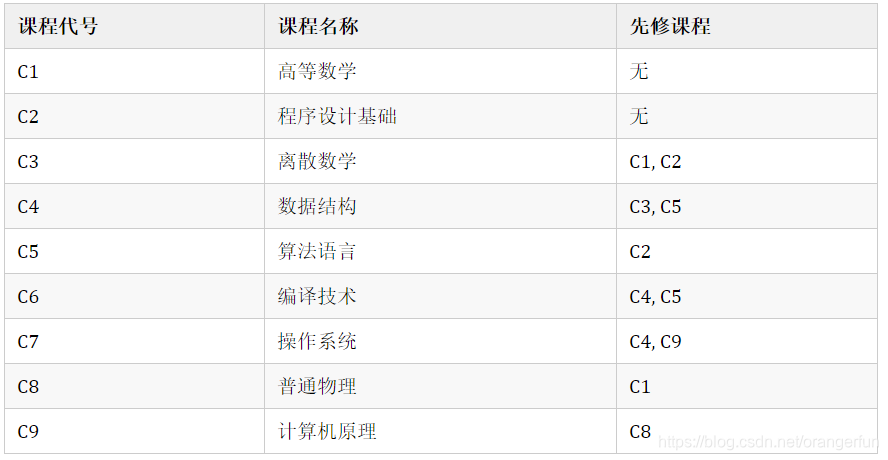
在这里插入图片描述
这里有 9 门课程，有些课程是有先修课程的要求的，就是你要先学了「最右侧这一栏要求的这个课」才能再去选「高阶」的课程。

画出图如下：
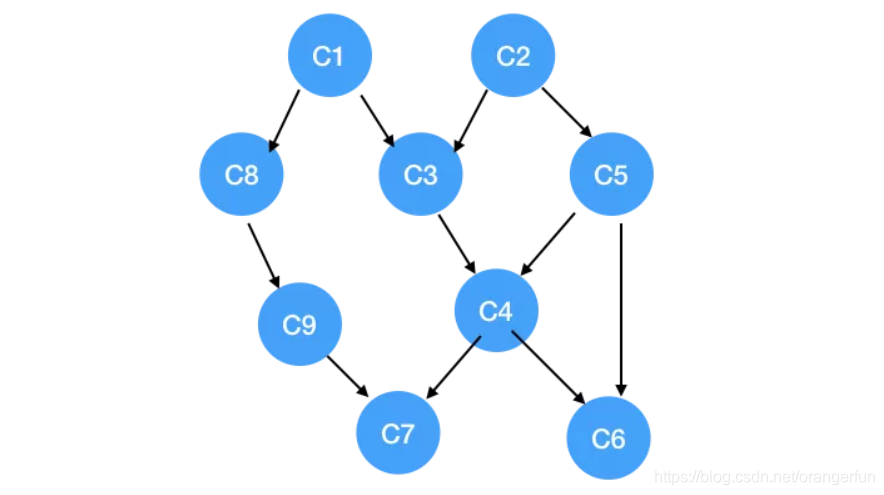
在这里插入图片描述
我们一眼可以看出来要先学 C1, C2，因为这两门课没有任何要求嘛，大一的时候就学呗；

大二就可以学第二行的 C3, C5, C8 了，因为这三门课的先修课程就是 C1, C2，我们都学完了；

大三可以学第三行的 C4, C9；

最后一年选剩下的 C6, C7。

这样，我们就把所有课程学完了，也就得到了这个图的一个拓扑排序。

4. 算法流程

为什么我们先看上了 C1, C2?因为它们没有依赖别人啊，也就是它的入度为 0

入度：顶点的入度是指「指向该顶点的边」的数量
出度：顶点的出度是指该顶点指向其他点的边的数量

step0:预处理得到每个点的入度
可以用一个 dict 来存放这个信息，或者用一个数组会更精巧；在文中为了方便展示，就用表格了：
在这里插入图片描述

step1
把入度为0的点放入一个queue中，然后就需要把某些点拿出去执行了，把 C1 拿出来执行，那这意味「以 C1 为顶点」的「指向其他点」的「边」都消失了，也就是 C1 的出度变成了 0.
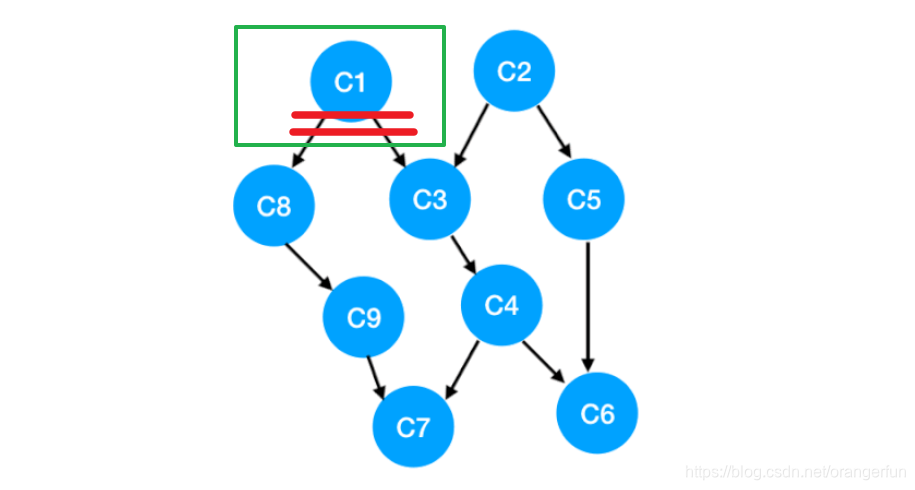
在这里插入图片描述
那么此时我们就可以更新 C1 所指向的那些点也就是 C3 和 C8 的入度了，更新后的数组如下：

C8 的入度变成了 0，也就意味着 C8 此时没有了任何依赖，可以放到我们的 queue 里等待执行了，此时我们的 queue 里就是：[C2, C8]

step2
下一个我们再执行 C2，C2 所指向的 C3, C5 的入度-1
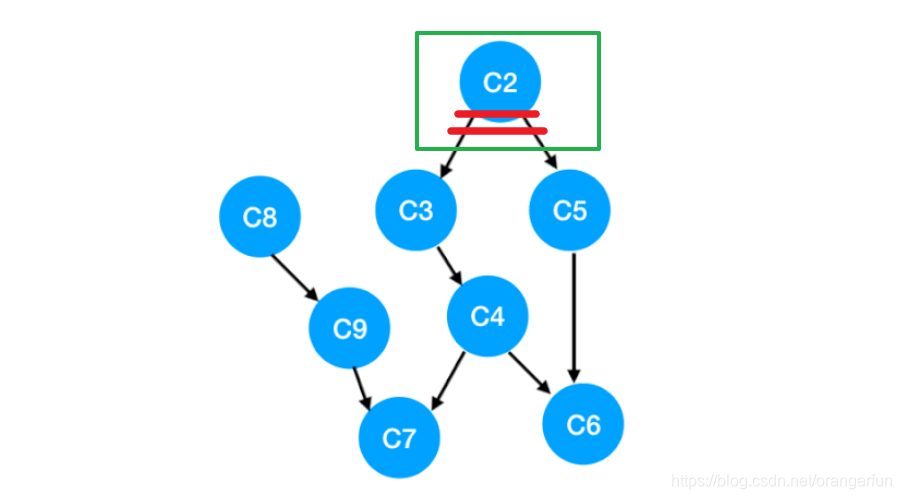
在这里插入图片描述
更新表格：

是 C3 和 C5 都没有了任何束缚，可以放进 queue 里执行了，queue 此时变成：[C8, C3, C5]

step3
如此继续执行，直到queue为空即可

总结
我们把入度为 0 的那些顶点放入 queue 中，然后通过每次执行 queue 中的顶点，就可以让依赖这个被执行的顶点的那些点的入度-1，如果有顶点的入度变成了 0，就可以放入 queue 了，直到 queue 为空。

当我们 check 是否有新的顶点的入度 == 0 时，没必要过一遍整个 map 或者数组，只需要 check 刚刚改动过的就好了

另一个是如果题目没有给这个图是 DAG 的条件的话，那么有可能是不存在可行解的，那怎么判断呢？很简单的一个方法就是比较一下最后结果中的顶点的个数和图中所有顶点的个数是否相等，或者加个计数器，如果不相等，说明就不存在有效解。所以这个算法也可以用来判断一个图是不是有向无环图。

5. 例题

现在你总共有 n 门课需要选，记为 0 到 n-1。

在选修某些课程之前需要一些先修课程。例如，想要学习课程 0 ，你需要先完成课程 1 ，我们用一个匹配来表示他们: [0,1]

给定课程总量以及它们的先决条件，返回你为了学完所有课程所安排的学习顺序。

可能会有多个正确的顺序，你只要返回一种就可以了。如果不可能完成所有课程，返回一个空数组。

例子：

输入: 2, [[1,0]] 
输出: [0,1]
解释: 总共有 2 门课程。要学习课程 1，你需要先完成课程 0。因此，正确的课程顺序为 [0,1] 。

输入: 4, [[1,0],[2,0],[3,1],[3,2]]
输出: [0,1,2,3] or [0,2,1,3]
解释: 总共有 4 门课程。要学习课程 3，你应该先完成课程 1 和课程 2。并且课程 1 和课程 2 都应该排在课程 0 之后。
     因此，一个正确的课程顺序是 [0,1,2,3] 。另一个正确的排序是 [0,2,1,3]

程序

class Solution:
    def findOrder(self, numCourses: int, prerequisites: List[List[int]]) -> List[int]:
        res = []
        in_degree = [0]*numCourses

        # 设置各个顶点的入度数
        for core in prerequisites:
            in_degree[core[0]] += 1
        
        # 设置起始queue
        queue = []
        for i in range(numCourses):
            if in_degree[i] == 0:
                queue.append(i)
        
        # 循环直到queue为空
        while queue:
            curr = queue.pop(0)
            res.append(curr)

            for item in prerequisites:
                if item[1] == curr:
                    in_degree[item[0]] -= 1
                    if in_degree[item[0]] == 0:
                        queue.append(item[0])
        # 最后输出时候比较结果中的节点数和实际节点数是否相同，若不同则说明有环，不能产生结果
        return res if len(res) == numCourses else []

reference

揭开「拓扑排序」的神秘面纱