数据结构：树的相关概念

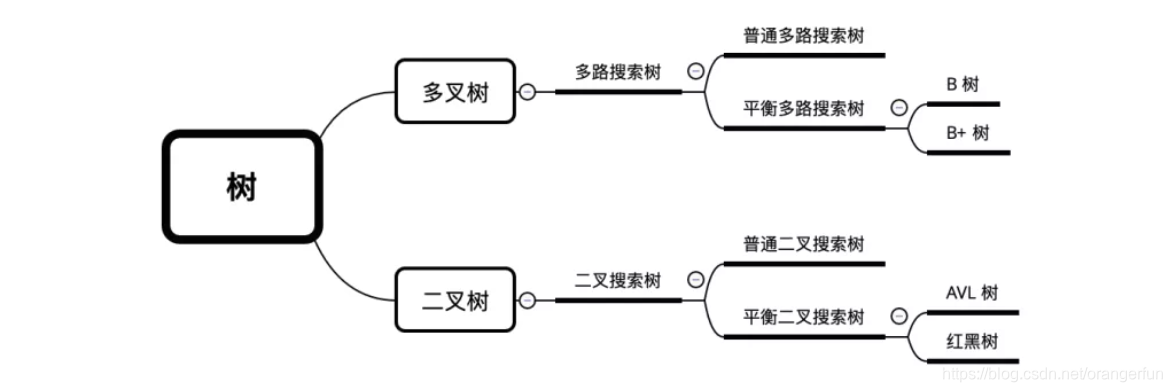
树的知识框架结构如下图所示：

1.平衡二叉搜索树

平衡二叉搜索树（Balanced Binary Search Tree），英文简称 BBST。经典常见的平衡二叉搜索树是AVL 树和红黑树

1.1 二叉搜索树

二叉搜索树（Binary Search Tree）是二叉树的一种，英文简称 BST。又称为二叉查找树、二叉排序树。
它的特点是任何一个结点的值都大于其左子树的所有结点的值，都小于其右子树的所有结点的值。

1.2 平衡

平衡（Balance）：就是当结点数量固定时，左右子树的高度越接近，这棵二叉树越平衡（高度越低）。而最理想的平衡就是完全二叉树/满二叉树，高度最小的二叉树。

一棵二叉搜索树平均时间复杂度可以认为是树的高度 O(h)。像左边这棵，结点的左右子树的高度接近，属于一棵平衡二叉搜索树，O(h) = O(logn)；而右边这棵，高度达到了最大，已经退化成了链表，O(h)=O(n)。

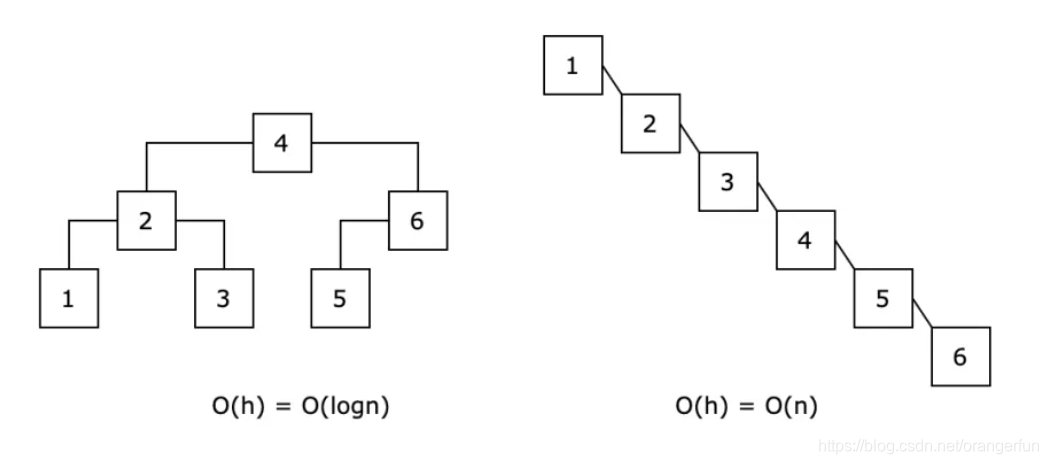
平衡二叉树就是任何节点的左右子树高度相差一的二叉树

1.3 AVL树

平衡因子（Balance Factor）：某结点的左右子树的高度差
每个叶子结点的平衡因子都是 0。看这棵二叉搜索树，红色数字标注了每个结点对应的平衡因子。

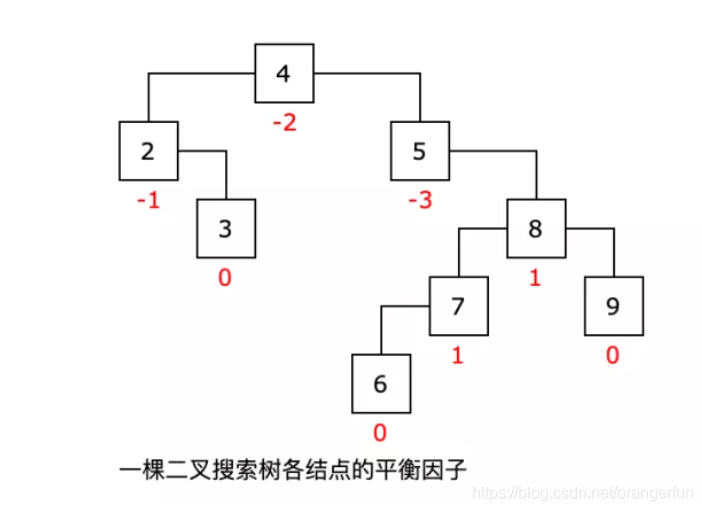
举例：8 的左子树高度为 2，右子树高度为 1，因此它的平衡因子为 1；5 的左子树高度为 0，右子树高度为 3，因此它的平衡因子为 -3；4 的左子树高度为 2，右子树高度为 4，因此它的平衡因子为 -2；

AVL 树具有以下特点：

• 每个结点的平衡因子只可能是 -1、0、1（如果绝对值超过 1，则认为是失衡）
• 每个结点的左右子树高度差不超过 1
• 搜索、插入、删除的时间复杂度是 O(logn)

如下是一棵AVL树

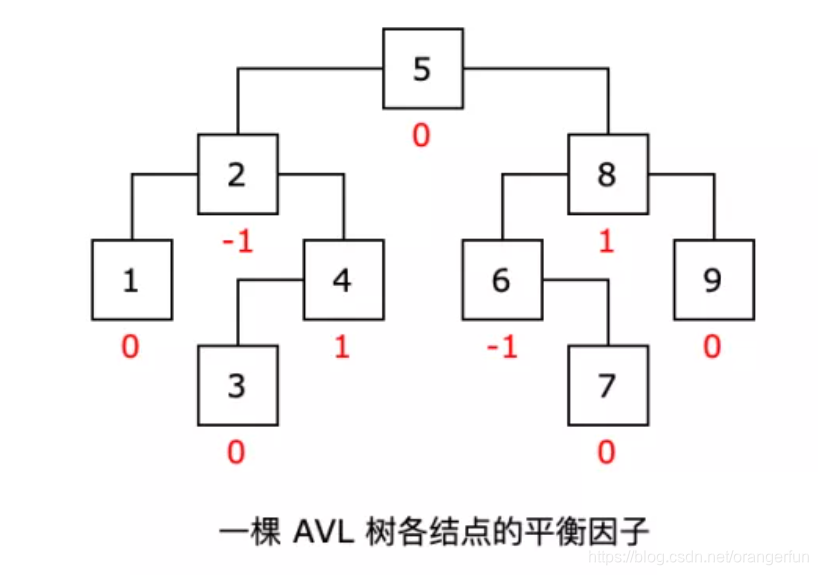
1.4 B树

B 树（Balanced Tree）是一种平衡的多路搜索树，特点如下：

• 1 个结点可以存储超过 2 个元素，可以拥有超过 2 个子结点
• 拥有二叉搜索树的一些性质
• 平衡，每个结点的所有子树高度一致
  

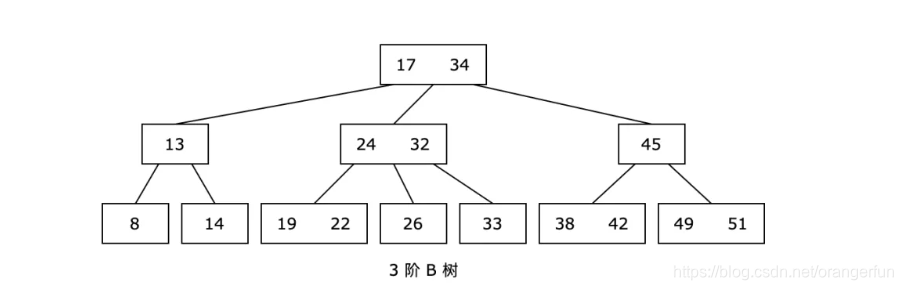
（1）m阶B树的性质
m 阶 B 树指的是一个结点最多拥有 m 个子结点。假设一个结点存储的元素个数为 x，那么如果这个结点是：
根节点：$1⩽x⩽m-1$
非根节点：ceiling(m / 2) - 1 ≤ x ≤ m - 1

如果有子结点，子结点个数为 y = x + 1，那么如果这个结点是：
根结点：2 ≤ y ≤ m
非根结点：ceiling(m / 2) ≤ y ≤ m

ceiling表示向上取整

2 红黑树

红黑树是一种含有红黑结点并能自平衡的二叉搜索树。

为了保证平衡，红黑树必须满足以下性质：

• 每个结点是要么是红色或黑色
• 根结点必须是黑色
• 叶结点（外部结点、空结点）是黑色
• 红色结点不能连续（也就是，红色结点的孩子和父亲都是黑色）
• 对于每个结点，从该点至 null（树尾端，Java 中为 null 的结点）的任何路径都包含所相同个数的黑色结点