二叉树算法精讲-优快云博客

本文深入解析二叉树的构建、遍历方法，包括深度优先（前序、中序、后序）与广度优先遍历，探讨子树、最大深度、平衡二叉树、最大路径和及直径等问题，提供详尽的代码实现。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

文章目录

1. 搜索二叉树建立
2. 二叉树深度优先遍历
3. 广度优先遍历
4. 另一棵树的子树-leetcode572
5. 二叉树的最大深度
6. 平衡二叉树
7. 二叉树中最大路径和
8. 二叉树的直径

1. 搜索二叉树建立

二叉搜索树：任意个节点，左节点比他小，右节点比他大

class TreeNode:
	def __init__(self, value):
		self.val = value
		self.left = None
		self.right = None

# 搜索二叉树的建立
def createTree(root, val):
	newnode = TreeNode(val)
	if root == None:
		root = newnode
		return root

	current = root
	while current != None:
		back = current
		if val < current.val:
			current = current.left
		else:
			current = current.right
	if val < back.val:
		back.left = newnode
	else:
		back.right = newnode
	return root

2. 二叉树深度优先遍历

树的深度优先遍历包含三种方法，分别是：

前序遍历（根左右）
中序遍历（左根右）
后序遍历（左右根）

区分这三种遍历方式主要看根的位置

而宽度优先的遍历方式主要是用队列，将节点存入，然后递归读取数据

具体实现见下方程序

2.1 前序遍历

递归方式

def preorder(root):
	if root != None:
		print(root.val, end="\t")
		preorder(root.left)
		preorder(root.right)

迭代方式

def preOder(root):
    if not root:
        return None
    ptr = root
    stack = []
    while ptr or stack:
        while ptr:
            print(ptr.value, end=" ")
            stack.append(ptr)
            ptr = ptr.left
        ptr = stack.pop()
        ptr = ptr.right

2.2 中序遍历

递归方式

def inorder(root):
	if root != None:
		inorder(root.left)
		print(root.val, end='\t')
		inorder(root.right)

迭代方式

def inOder(root):
    if not root:
        return None
    ptr = root
    stack = []
    while ptr or stack:
        while ptr:
            stack.append(ptr)
            ptr = ptr.left
        ptr = stack.pop()
        print(ptr.value, end=" ")
        ptr = ptr.right

2.3 后序遍历

递归方式

def postOrder(root):
	if root != None:
		postOrder(root.left)
		postOrder(root.right)
		print(root.val, end="\t")

迭代方式

def BehindOrder(root):
    if not root:
        return
    stack1 = []
    stack2 = []
    stack1.append(root)
    while stack1:
        node = stack1.pop()
        if node.left:
            stack1.append(node.left)
        if node.right:
            stack1.append(node.right)
        stack2.append(node)
    while stack2:
        print(stack2.pop().value, end=" ")

方法2（推荐）
后序遍历迭代和前序遍历的区别是把 left/right 互换，最后再把获得的数据逆序输出，前序遍历根左右 left/right互换后根右左, 最后逆序输出左右根即后序遍历

def postorderTraversal(self, root):
        T = root
        stack = []
        postData = []
        while (T or stack):
            while T:
                stack.append(T)
                postData.append(T.val)
                T = T.right               # 先 right，再 left
            if stack:
                T = stack.pop()
                T = T.left
        return postData[::-1]             # 最后逆序输出

3. 广度优先遍历

# 广度优先遍历
def bfs(root):
	nodes = [root]
	result = []
	while nodes:
		node = nodes.pop()
		result.append(node.val)
		if node.left != None:
			nodes.insert(0, node.left)
		if node.right != None:
			nodes.insert(0, node.right)
	print(result)

4. 另一棵树的子树-leetcode572

给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在，返回 true ；否则，返回 false 。

二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。

注意与子结构区分：剑指offer-17.树的子结构

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def isSubtree(self, root: TreeNode, subRoot: TreeNode) -> bool:
        if root == None and subRoot == None:
            return True
        elif root == None or subRoot == None:
            return False

        def help(root, subRoot):
            if root == None and subRoot == None:
                return True
            elif subRoot == None or root == None:
                return False

            if root.val == subRoot.val:
                return help(root.left, subRoot.left) and help(root.right, subRoot.right)
            else:
                return False
                
        return help(root, subRoot) or self.isSubtree(root.left, subRoot) or self.isSubtree(root.right, subRoot)

5. 二叉树的最大深度

leetcode 104
给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

1. 递归：深度优先搜索

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        if root == None:
            return 0
        else:
            return max(self.maxDepth(root.left), self.maxDepth(root.right))+1

时间复杂度：每个结点只访问一次，因此时间复杂度为 $O (N)$ ，其中 N是结点的数量

2. 广度优先：方法1

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        if root == None:
            return 0
        nodes = [[1, root]]
        maxdepth = 0
        while nodes:
            node = nodes.pop(0)
            maxdepth = max(maxdepth, node[0])
            if node[1].left:
                nodes.append([maxdepth+1, node[1].left])
            if node[1].right:
                nodes.append([maxdepth+1, node[1].right])
        return maxdepth

3. 广度优先：方法2（推荐）

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        if root == None:
            return 0
        
        nodes = [root]
        depth = 0
        while nodes:
            depth += 1
            for i in range(len(nodes)):
                no = nodes.pop(0)
                if no.left:
                    nodes.append(no.left)
                if no.right:
                    nodes.append(no.right)
        return depth

6. 平衡二叉树

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：一个二叉树每个节点的左右两个子树的高度差的绝对值不超过 1

1. 暴力法
从顶到底判断每一个节点为根节点的子树是否为平衡二叉树

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def isBalanced(self, root: TreeNode) -> bool:

        def getDepth(root):
            if root == None:
                return 0
            else:
                return max(getDepth(root.left), getDepth(root.right))+1
        
        if root == None:
            return True
        if abs(getDepth(root.left)-getDepth(root.right))>1:
            return False
        else:
            return self.isBalanced(root.left) and self.isBalanced(root.right)

时间复杂度： $N l o g (N)$
isBalanced(root) 遍历树所有节点， $O (N)$ ，遍历每个节点时需要计算该子树的高度 $l o g (N)$ ，合起来为 $O (N l o g (N))$
二分查找的时间复杂度为什么是O(logn)

方法2: 从下往上（推荐）
递归到最底层，然后往上合并：
left == -1:表示左子树不平衡直接返回
right == -1: 表示右子树不平衡直接返回
abs(left-right)>2: 表示以当前节点为根节点的树不平衡

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def isBalanced(self, root: TreeNode) -> bool:

        def help(root):
            if root == None:
                return 0
            left = help(root.left)
            right = help(root.right)
            if left == -1 or right == -1 or abs(left-right)>1:
                return -1
            else:
                return max(left,right)+1    # 返回当前节点的最大深度
        
        res = help(root)
        return res != -1

时间复杂度： $O (n)$

7. 二叉树中最大路径和

leetcode 124

路径被定义为一条从树中任意节点出发，沿父节点-子节点连接，达到任意节点的序列。同一个节点在一条路径序列中至多出现一次。该路径至少包含一个节点，且不一定经过根节点。

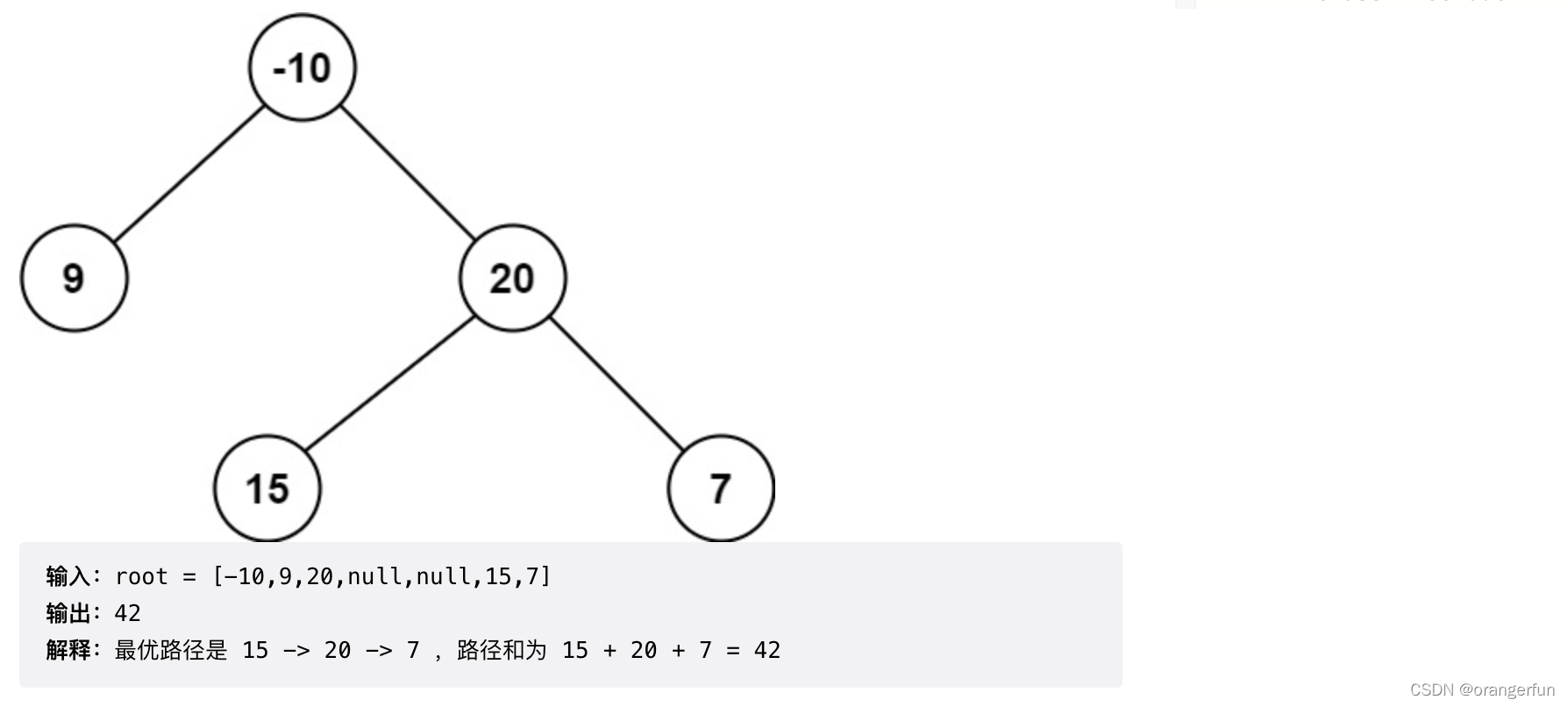
在这里插入图片描述
思路
统计以每个节点为root节点的路径，然后取出最大路径作为最后结果

空节点的最大贡献值等于 0
非空节点的最大贡献值等于节点值与其子节点中的最大贡献值之和（对于叶节点而言，最大贡献值等于节点值）

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def __init__(self):
        self.res = -float("inf")
    def maxPathSum(self, root: Optional[TreeNode]) -> int:
        if root == None:
            return 0

        def help(root):
            if root == None:
                return 0
             # 左子节点的贡献值：注意如果为负则取0
            left = max(help(root.left),0)
            # 右子节点的贡献值
            right = max(help(root.right), 0)
            # 最大路径
            self.res = max(self.res, root.val+left+right)
            # 返回当前节点的贡献值
            return root.val + max(left,right)
        
        tmp = help(root)
        return self.res

8. 二叉树的直径

二叉树的直径
给定一棵二叉树，你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。

返回 3, 它的长度是路径 [4,2,1,3] 或者 [5,2,1,3]

1. 深度优先
一条路径的长度为该路径经过的节点数减一，所以求直径（即求路径长度的最大值）等效于求路径经过节点数的最大值减一。

任意一条路径都可以看作是：左子树中最长路径+右子树最长路径+1

空节点路径长度为0
非空节点：left+right+1
遍历每个节点，获取最长的一个

# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def diameterOfBinaryTree(self, root: TreeNode) -> int:
        if root == None:
            return 0
        maxlen = -float("inf")
        def help(root):
            nonlocal maxlen
            if root == None:
                return 0
            left = help(root.left)
            right = help(root.right)
            maxlen = max(maxlen, left+right+1)
            # 当前节点对其父节点的贡献值
            return max(left, right)+1
        help(root)
        return maxlen-1