机器学习中偏差和方差的区别

今天在看L1和L2正则的相关知识时，看到这样一段话：

        L2与L1的区别在于，L1正则是拉普拉斯先验，而L2正则则是高斯先验。它们都是服从均值为0，协方差为1λ。当λ=0时，即没有先验）没有正则项，则相当于先验分布具有无穷大的协方差，那么这个先验约束则会非常弱，模型为了拟合所有的训练集数据， 参数w可以变得任意大从而使得模型不稳定，即方差大而偏差小。λ越大，标明先验分布协方差越小，偏差越大，模型越稳定。即，加入正则项是在偏差bias与方差variance之间做平衡tradeoff。

        让我很困惑的是为什么参数w任意大时模型不稳定会出现方差大偏差小的情况，那么方差和偏差作为两种度量方式有什么区别呢？

        首先看了下百度百科中偏差的解释为：偏差又称为表观误差，是指个别测定值与测定的平均值之差。感觉这个解释并不太应用于机器学习中，那么这句话在机器学习中的意思应该是预测值与真实值之间的距离。

        在知乎上看到了几种解释，还是比较有助于自己理解的：

         1、偏差：描述的是预测值（估计值）的期望与真实值之间的差距。偏差越大，越偏离真实数据，如下图第二行所示。

              方差：描述的是预测值的变化范围，离散程度，也就是离其期望值的距离。方差越大，数据的分布越分散，如下图右列所示。

 

2、从上面的解释仅仅能够知道偏差和方差的区别，还是不能够解释文章开始提出的问题，再来看下面这个解释：

Bias：误差，对象是单个模型，期望输出与真实标记的差别（可以解释为描述了模型对本训练集的拟合程度）

Variance：方差，对象是多个模型（这里更好的解释是换同样规模的训练集，模型的拟合程度怎么样；也可以说方差是刻画数据扰动对模型的影响，描述的是训练结果的分散程度）
从同一个数据集中，用科学的采样方法得到几个不同的子训练集，用这些训练集训练得到的模型往往并不相同。

 

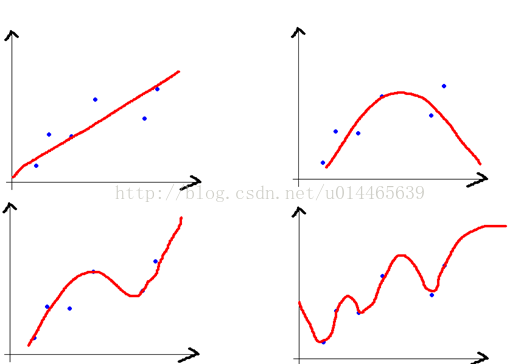
以上图为例：
1. 左上的模型偏差最大，右下的模型偏差最小；
2. 左上的模型方差最小，右下的模型方差最大（根据上面红字的解释这里就很好理解了）

一般来说，偏差、方差和模型的复杂度之间的关系是这样的：

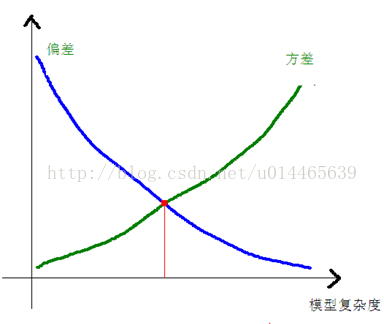
实际中，我们需要找到偏差和方差都较小的点。

XGBOOST中，我们选择尽可能多的树，尽可能深的层，来减少模型的偏差；
通过cross-validation，通过在验证集上校验，通过正则化，来减少模型的方差

从而获得较低的泛化误差。