剑指offer：数组中出现次数超过一半的数字

题目描述

数组中有一个数字出现的次数超过数组长度的一半，请找出这个数字。例如输入一个长度为9的数组{1,2,3,2,2,2,5,4,2}。由于数字2在数组中出现了5次，超过数组长度的一半，因此输出2。如果不存在则输出0。

思路一：拿到题目，首先想到的是可以遍历一遍数组，把数组中出现元素及其出现的次数存入一个字典当中，这样遍历完成后就可以很快获得出现次数最多的元素，并比较它的出现次数是否是数组长度的一半。

一、用HashMap实现

 

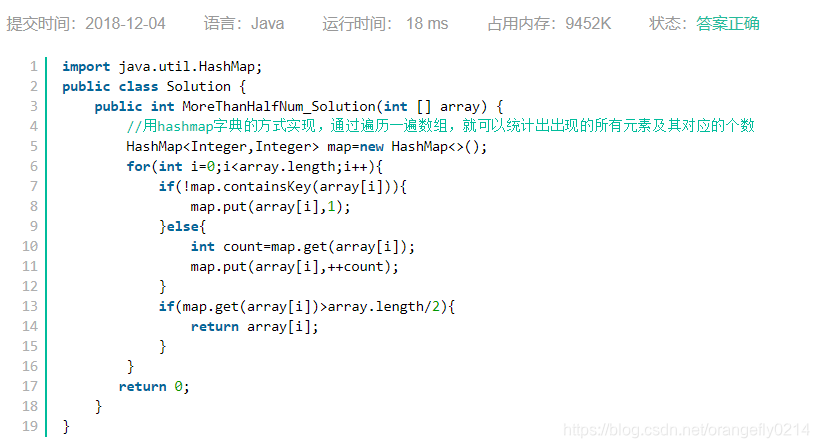
思路二、观察数组的特点

数组中一个数字出现的次数超过数组长度的一半，则这个数字出现的次数比其他所有数字出现的和还要多。

我们可以根据以下步骤来实现统计：

step1:从头向后遍历数组，记录元素和次数，如果后一个数和前一个数相等，则次数+1，否则，次数-1；
step2:如果次数为0，则保留当前最新的这个元素并将其次数置位1；经过这个遍历，可以统计出数组中出现次数最多的那个数。
step3:遍历数组，计算出现次数最多的这个数的出现次数，如果它比数组长度的一半大，则返回这个数，否则返回0.

二、观察数组的特点

 

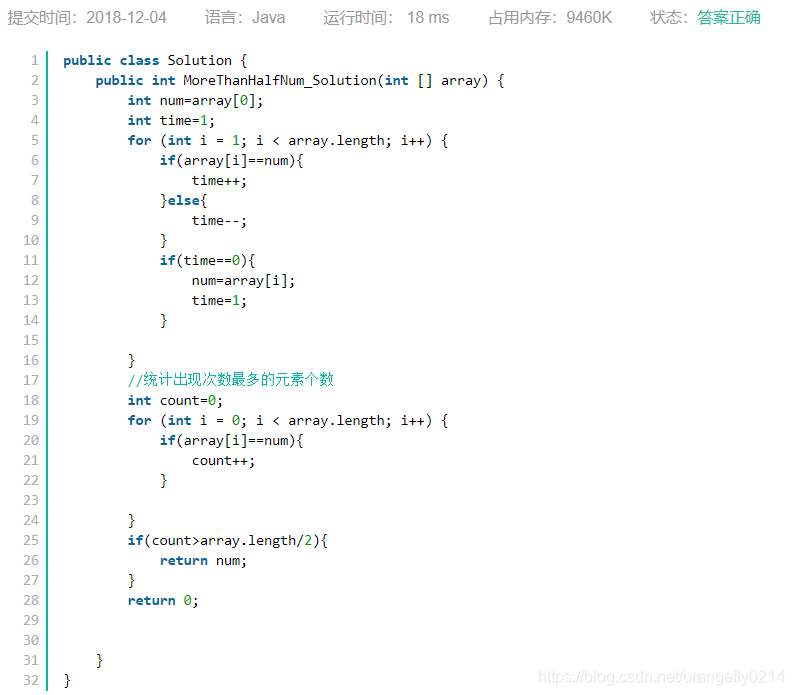
解法三、

对数组进行排序，则在已排序的数组中，位于中间位置的元素即为出现次数大于数组长度一半的数。

我们可以用java自带的排序功能。

三、排序后直接比较

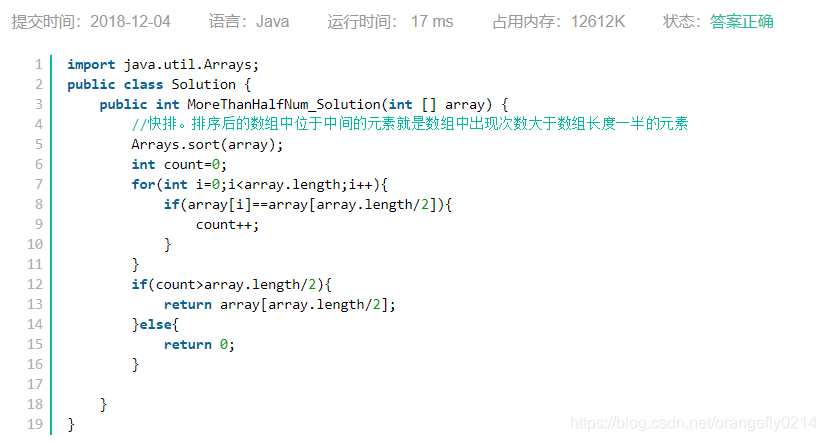
解法四、利用快速排序

对数组进行排序，排序后数组的中位数即为数组中出现次数大于数组长度一半的元素。

根据快排算法的思想，从数组中随机选取一个数，调整数组元素的顺序，使得比这个数小的数都位于该数的左边，比它大的数都位于这个数的右边。调整后如果选中这个数的下标刚好是n/2，则这个数就是中位数。如果下标大于n/2，则中位数位于它的左边，我们接着在左半边中查找；如果下标小于n/2，则中位数位于它的右边，则接着在右边部分的数组中查找。依次递归，直到选取的这个数的排序后的下标等于n/2.

实现如下：

实现1：

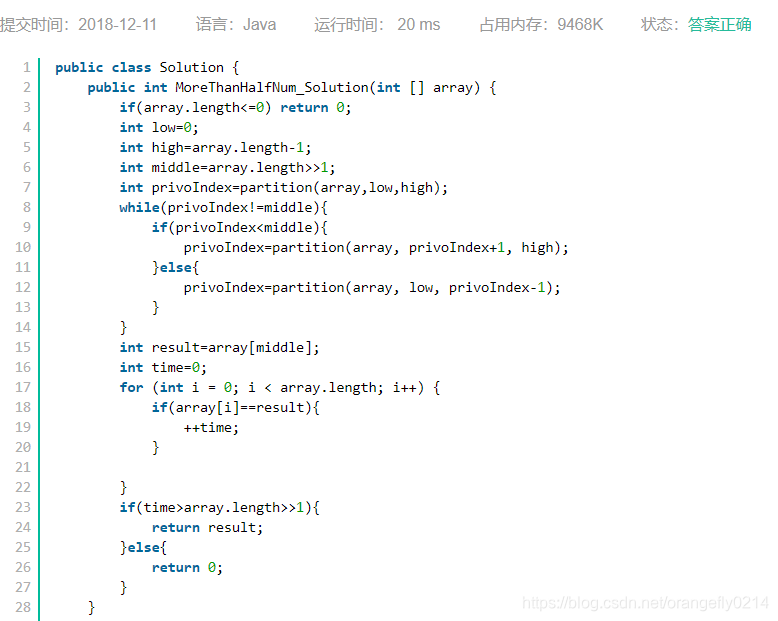
一个指针实现的partition函数

  

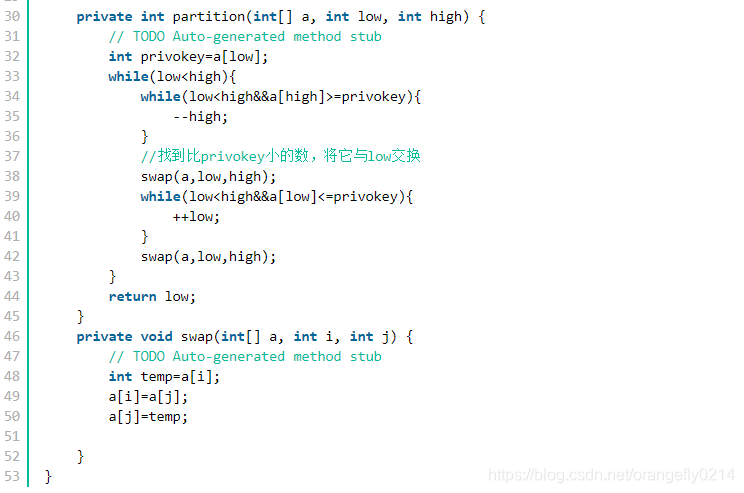
实现2：

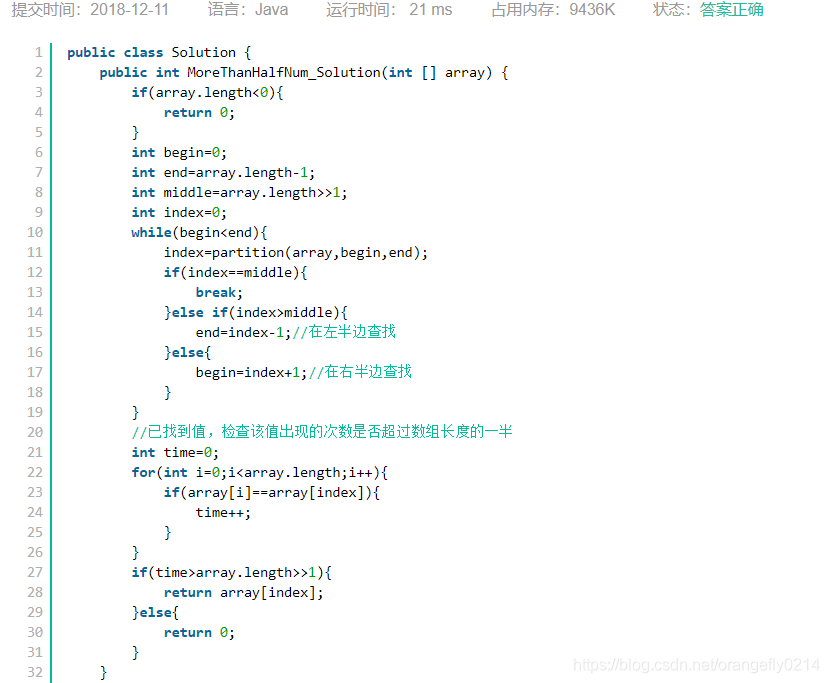
两个指针实现partition函数

    

 

 

 

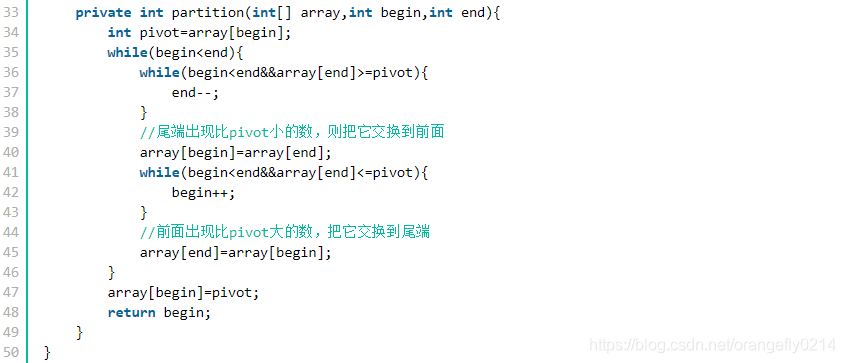
快速排序中的Partition函数的参考博客：

https://blog.youkuaiyun.com/u013457167/article/details/79749882

https://blog.youkuaiyun.com/tianyuxingxuan/article/details/77331032