《2018年2月12日》【连续124天】
标题:信息熵H和模拟日历;
内容:
A.简单了解了一下香农的信息熵H:
先设随机事件发生的不确定性为发生概率pi的函数f(pi),该函数具有如下三条性质:
1)单调性:概率越大的事件,信息熵越小,反之亦然。即,
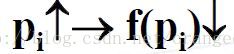
2)非负性:f(pi)非负;
3)可加性:多随机事件同时发生存在的总不确定性的度量,可以表示为各时间不确定性度量的和。例:

香农在《通信的数学理论》中证得: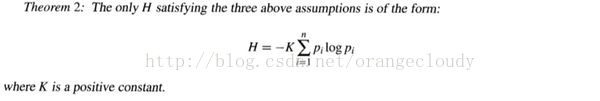
H即为信息熵;
B.练习了模拟日历:
import java.text.DateFormatSymbols;
import java.util.*;
public class CalenderTest {
//模拟日历
public static void main(String[] args) {
GregorianCalendar d =new GregorianCalendar();
//得到现在的日,月
int today =d.get(Calendar.DAY_OF_MONTH);
int month =d.get(Calendar.MONTH);
//设置第一天
d.set(Calendar.DAY_OF_MONTH,1);
//得到第一天是星期几
int weekday =d.get(Calendar.DAY_OF_WEEK);
//得到一个星期的开始(例如,欧洲一般为星期一,美国一般为星期天)
int firstDayOfweek =d.getFirstDayOfWeek();
//使得每月的第一日自动对齐
int indent =0;
while(weekday !=firstDayOfweek)
{
indent++;
d.add(Calendar.DAY_OF_MONTH, -1);
weekday =d.get(Calendar.DAY_OF_WEEK);
}
String[] WeekdayNames =new DateFormatSymbols().getShortWeekdays();
do
{
System.out.printf("%4s", WeekdayNames[weekday]);
System.out.print(" ");
d.add(Calendar.DAY_OF_MONTH, 1);
weekday =d.get(Calendar.DAY_OF_WEEK);
}
while(weekday !=firstDayOfweek);
System.out.println();
for(int i=1;i<=indent;i++)
{
System.out.print(" ");
}
d.set(Calendar.DAY_OF_MONTH, 1);
do
{
int day =d.get(Calendar.DAY_OF_MONTH);
System.out.printf("%3d",day);
//将今天标记*
if(day==today)System.out.print("*");
else System.out.print(" ");
d.add(Calendar.DAY_OF_MONTH, 1);
weekday =d.get(Calendar.DAY_OF_WEEK);
if(weekday==firstDayOfweek)System.out.println();
}
while(d.get(Calendar.MONTH)==month);
if(weekday!=firstDayOfweek)System.out.println();
}
}
效果如下:
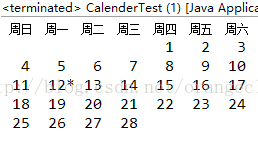




 本文介绍了香农信息熵的基本概念及其特性,并通过Java代码实现了模拟日历功能,能够显示当前月份的日历并标记当天日期。
本文介绍了香农信息熵的基本概念及其特性,并通过Java代码实现了模拟日历功能,能够显示当前月份的日历并标记当天日期。
















 760
760

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








