032day(STL中的二分查找算法)

《2017年11月11日》【连续032天】

标题：STL中的二分查找算法；

内容：A.观看MOOC12.2；

B.

binary_search:

（一）在从小到大排好序的基本类型数组上进行二分查找；

binary_search(数组名+n1,数组名+n2,值);

区间[n1,n2),下标为n2的元素不在查找区间（可对照031day）；

在该区间内查找“等于”“值”的元素，返回值为ture（找到）或false（未找到）；

“等于”的含义：a 等于 b <=> a<b和b<a都不成立       注：a等于b并不是 a==b;

（二）在自定义排序规则排好序的，元素为任意的T类型的数组中进行二分查找；

binary_search(数组名+n1,数组名+n2,值,排序规则结构名());

区间[n1,n2)；

在该区间内查找“等于”“值”的元素，返回值为ture（找到）或false（未找到）；

查找时的排序规则，必须和排序时的规则一致！

“等于”的含义：a 等于 b <=>“a必须在b前面”和“b必须在a前面”都不成立；

struct Rule{   //按个位数从小到大排序 
bool operator()(const int & a1,const int & a2){
return a1%10<a2%10;
}
}; 
void Print(int a[],int size){
for(int i=0;i<size;++i){
cout<<a[i]<<" ";
}
cout<<endl;
} 
int main()
{
int a[]={12,45,3,98,21,7};
sort(a,a+6);
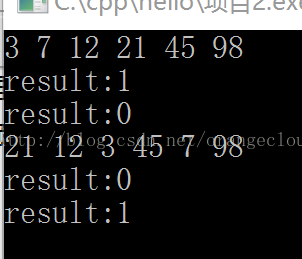
Print(a,6);
cout<<"result:"<<binary_search(a,a+6,12)<<endl;
cout<<"result:"<<binary_search(a,a+6,77)<<endl;
sort(a,a+6,Rule());
Print(a,6);
cout<<"result:"<<binary_search(a,a+6,7)<<endl;
    cout<<"result:"<<binary_search(a,a+6,8,Rule())<<endl; //98和8在此排序结构下满足等于的条件；

lower_bound:二分查找下界：

（一）在对元素类型为T的从小到大排好序的数组中进行查找：

T * lower_bound(数组名+n1,数组名+n2,值);

返回一个指针 T * p;

区间[n1,n2);

*p是查找区间里下标最小的，大于等于“值”的元素。如果找不到，p指向下标为n2的元素；

（二）在元素为任意的T类型，按照自定义排序规则排好序的数组中进行查找：

T*lower_bound(数组名+n1,数组名+n2,值,排序规则结构名());

返回一个指针 T*p;

*p是查找区间下标最小的，按自定义排序规则，可以排在“值”后面的元素，如果找不到，p指向下标为n2的元素；

upper_bound:二分查找找上界；

（一）元素类型为T，从小到大排好序的数组中查找：

T*upper_bound(数组名+n1,数组名+n2,值)；

 

返回一个指针 T * p;

*p是查找区间里下标最小的，大于“值”的元素。如果找不到，p指向下标为n2的元素；

（二）在元素为任意的T类型，按照自定义排序规则排好序的数组中进行查找：

T*upper_bound(数组名+n1,数组名+n2,值,排序规则结构名());

*p是查找区间下标最小的，按自定义排序规则，必须排在“值”后面的元素，如果找不到，p指向下标为n2的元素；

#define NUM 7
int main()
{
int a[NUM]={12,5,3,5,98,21,7};
sort(a,a+NUM);
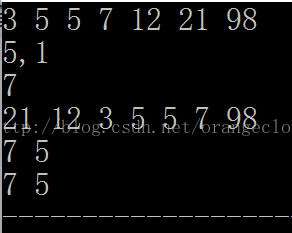
Print(a,NUM);
int*p=lower_bound(a,a+NUM,5);
cout<<*p<<","<<p-a<<endl;
p=upper_bound(a,a+NUM,5);
cout<<*p<<endl;
sort(a,a+NUM,Rule());
Print(a,NUM);
    p=lower_bound(a,a+NUM,16,Rule());
cout<<*p<<" "<<p-a<<endl;
p=upper_bound(a,a+NUM,5,Rule());
cout<<*p<<" "<<p-a;

明日计划：学习multiset;