RFC9474详解：RSA 盲签名协议的标准化与隐私保护实践

标准原文：https://www.rfc-editor.org/rfc/rfc9474.pdf

1. 引言：RSA 盲签名的起源与标准化价值

RSA 盲签名由 Chaum 于 1983 年在数字现金系统中首次提出，核心目标是实现 “签名者不可追踪消息，验证者可公开验证签名” 的隐私保护特性 [Chaum83]。随着隐私计算技术的发展，其应用已从最初的 “不可追踪支付” 扩展到 Apple Private Relay、Google VPN、Privacy Pass 等场景，成为解决 “隐私与可验证性平衡” 的关键技术。

然而，此前 RSA 盲签名缺乏统一标准，导致不同实现间兼容性差、安全边界模糊。2023 年 10 月发布的 RFC 9474（由 Fastly、Apple、Cloudflare 联合主导）填补了这一空白：该文档由 IRTF Crypto Forum Research Group（CFRG）共识制定，定义了基于 RSA-PSS 编码的盲签名协议（RSABSSA），且最终签名可通过标准 RSA-PSS 库验证，极大降低了部署门槛。

与 Verifiable Oblivious Pseudorandom Functions（VOPRF）相比，RSA 盲签名具有显著优势：VOPRF 需验证者持有私钥才能验证结果，而 RSA 盲签名仅需公钥即可完成验证，避免了私钥分发风险，尤其适合硬件安全模块（HSM）场景下的性能优化 [VOPRF][PRIVACY-PASS]。

2. 核心概念与关键术语

2.1 盲签名的核心特性

RSA 盲签名是一种两方协议，参与方包括客户端（持有待签名消息）和服务器（持有 RSA 密钥对），需满足两大核心属性：

• 盲性：服务器无法通过 “盲化消息” 和 “盲化签名” 反推原始消息内容；

• 公开可验证性：任何持有服务器公钥的实体，均可验证签名有效性，无需访问私钥。

2.2 关键术语与函数定义

RFC 9474 复用了 RFC 8017（PKCS #1 v2.2）的核心函数，并补充了协议专属术语，核心定义如下：

术语 / 函数	含义说明
bytes_to_int/int_to_bytes	字节串与整数的转换，对应 RFC 8017 的 OS2IP/I2OSP，采用大端序
EMSA-PSS-ENCODE	RSA-PSS 消息编码函数，输入消息、模数位数、哈希函数等，输出编码后的整数
RSASP1(sk, m)	RSA 私钥签名函数，用私钥sk对整数m签名，输出签名s
RSAVP1(pk, s)	RSA 公钥验证函数，用公钥pk对签名s解包，输出整数m
Prepare(msg)	消息预处理函数，分 “身份准备”（直接返回msg）和 “随机准备”（加 32 字节随机前缀）
Blind(pk, msg)	客户端盲化操作，生成盲化消息blinded_msg和盲化因子的模逆inv
BlindSign(sk, blinded_msg)	服务器盲签名操作，对盲化消息签名并验证正确性
Finalize(pk, msg, blind_sig, inv)	客户端解盲并验证签名，输出最终签名sig

3. RSA 盲签名协议完整流程

RFC 9474 定义的协议为一轮交互，客户端与服务器通过四步函数完成签名生成，流程如图 1 所示，核心细节如下：

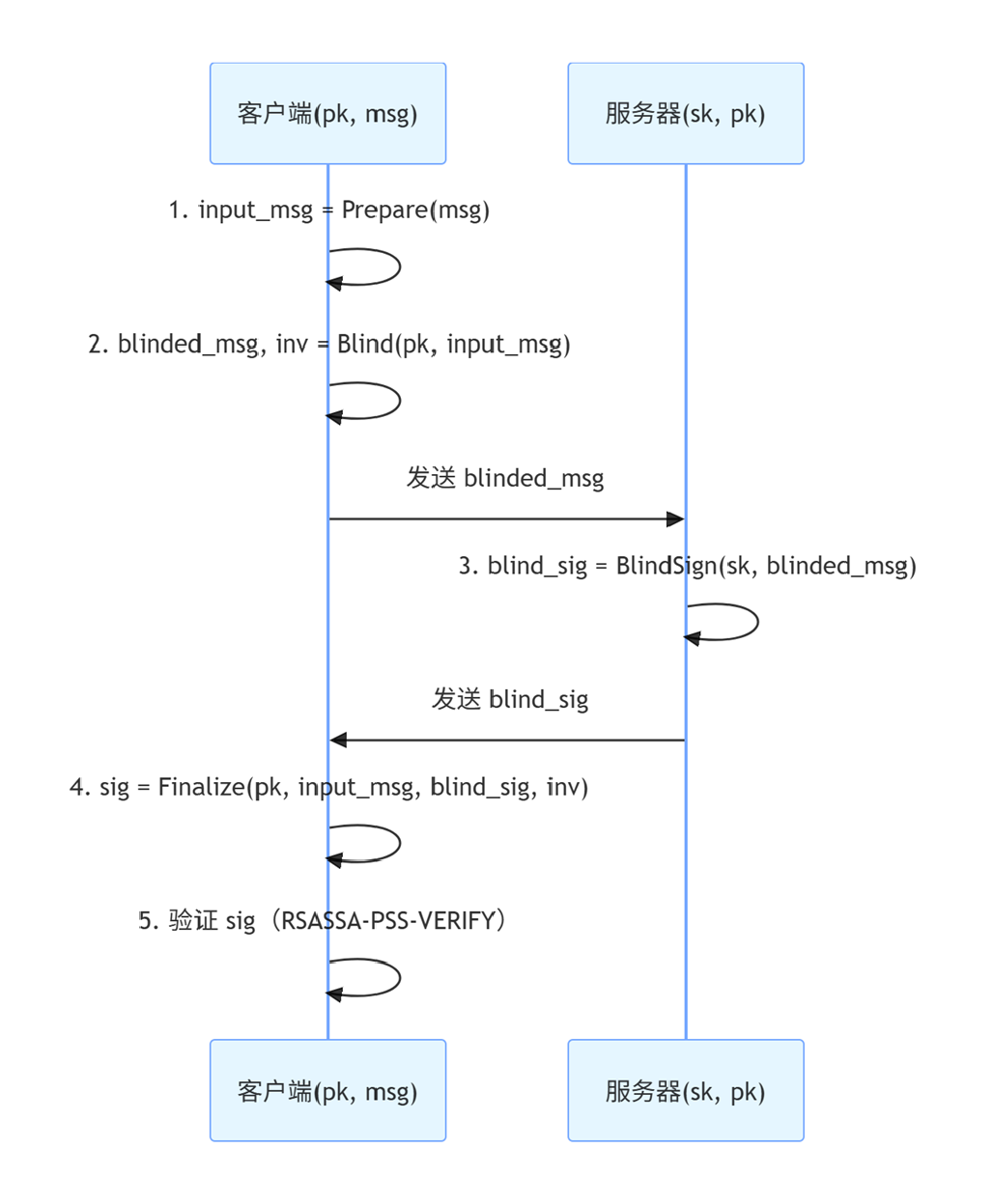
图 1：RSA 盲签名协议交互流程

3.1 步骤 1：消息预处理（Prepare）

根据应用场景选择预处理方式，核心差异在于是否注入随机熵：

• 身份预处理（PrepareIdentity）：input_msg = msg，适用于高熵消息（如随机生成的令牌），签名结果具有确定性；

• 随机预处理（PrepareRandomize）：生成 32 字节随机前缀msg_prefix，input_msg = concat(msg_prefix, msg)，适用于低熵消息（如用户 ID），可防止恶意服务器通过无效公钥窃取消息信息（见 7.3 节）。

3.2 步骤 2：客户端盲化（Blind）

盲化是协议的核心，需确保服务器无法关联blinded_msg与原始消息，步骤如下：

1. 消息编码：调用EMSA-PSS-ENCODE(msg, bit_len(n))，使用指定哈希函数（如 SHA-384）、掩码生成函数（MGF1）和盐长度（如 48 字节），若编码失败（如消息过长）则抛出错误；
2. 整数转换：m = bytes_to_int(encoded_msg)，验证m与模数n互质（否则抛出 “invalid input”）；
3. 盲化因子生成：生成随机整数r ∈ [1, n)，计算其模n的逆元inv = inverse_mod(r, n)（若逆元不存在，抛出 “blinding error”，需重试）；
4. 盲化计算：x = RSAVP1(pk, r)（公钥加密r），z = (m * x) mod n，最终blinded_msg = int_to_bytes(z, modulus_len)。

3.3 步骤 3：服务器盲签名（BlindSign）

服务器仅对盲化消息签名，无法获取原始消息，且需防护故障攻击：

1. 整数转换：m = bytes_to_int(blinded_msg)，验证0 ≤ m < n（否则抛出 “message representative out of range”）；
2. 私钥签名：s = RSASP1(sk, m)（私钥解密m，即签名）；
3. 正确性验证：m' = RSAVP1(pk, s)，若m' ≠ m，抛出 “signing failure”（防故障攻击，避免私钥泄露 [FAULTS]）；
4. 结果编码：blind_sig = int_to_bytes(s, modulus_len)，返回给客户端。

3.4 步骤 4：客户端解盲与验证（Finalize）

客户端解盲后需验证签名有效性，确保服务器未篡改结果：

1. 输入校验：检查blind_sig长度是否等于modulus_len（否则抛出 “unexpected input size”）；
2. 解盲计算：z = bytes_to_int(blind_sig)，s = (z * inv) mod n（用inv解盲），sig = int_to_bytes(s, modulus_len)；
3. 签名验证：调用RSASSA-PSS-VERIFY(pk, msg, sig)，验证通过则输出sig，否则抛出 “invalid signature”。

3.5 最终验证（Verification）

应用层需根据预处理方式调整验证逻辑：

• 若用PrepareIdentity：直接验证sig对msg的有效性；

• 若用PrepareRandomize：提取msg = slice(input_msg, 32, len(input_msg))，验证sig对input_msg的有效性后，再使用原始msg。

4. RSABSSA 协议变体：适配不同场景

RFC 9474 定义了 4 种标准化变体（RSABSSA），核心差异在于 “熵注入方式” 和 “签名确定性”，需根据消息熵和应用需求选择：

变体名称	哈希函数	MGF 函数	盐长度（sLen）	预处理函数	核心特性
RSABSSA-SHA384-PSS-Randomized	SHA-384	MGF1-SHA384	48 字节	PrepareRandomize	随机签名，高安全性（推荐）
RSABSSA-SHA384-PSSZERO-Randomized	SHA-384	MGF1-SHA384	0 字节	PrepareRandomize	随机签名，低计算开销
RSABSSA-SHA384-PSS-Deterministic	SHA-384	MGF1-SHA384	48 字节	PrepareIdentity	确定性签名，仅适用于高熵消息
RSABSSA-SHA384-PSSZERO-Deterministic	SHA-384	MGF1-SHA384	0 字节	PrepareIdentity	确定性签名，最低计算开销

推荐实践：除非应用强制要求确定性签名（如离线验证），否则优先选择PSS-Randomized或PSSZERO-Randomized，通过随机前缀抵御低熵消息泄露风险（见 7.3 节）。

5. 实现要点：从规范到工程落地

5.1 错误处理

协议各步骤均可能抛出错误，需按规范处理：

• Blind 函数错误：“blinding error”（逆元不存在）需重试（更换r），“invalid input” 需检查公钥有效性；

• BlindSign 函数错误：“signing failure” 需排查私钥完整性（如 HSM 故障），“message representative out of range” 需拒绝客户端请求；

• Finalize 函数错误：“invalid signature” 需重新发起协议，“unexpected input size” 需验证客户端输入合法性。

5.2 密钥管理

• 密钥生成：需符合 FIPS 186-5 标准，模数长度建议不低于 2048 位（推荐 4096 位）；

• 密钥隔离：RSABSSA 密钥不得复用于其他协议（如普通 RSA 签名），不同变体（如 PSS 与 PSSZERO）需使用独立密钥对；

• 证书配置：公钥若通过 X.509 证书分发，需使用id-RSASSA-PSS OID（RFC 5756），禁止使用rsaEncryption OID（RFC 5280），避免协议混淆。

6. 安全考量：规避核心风险

RFC 9474 专章强调安全边界，工程实现需重点关注以下威胁：

6.1 计时侧信道与故障攻击

• 计时侧信道：BlindSign 的RSASP1操作易受计时攻击（如通过计算时间推断私钥），需实现恒定时间算法（如 RSA blinding [TimingAttacks]）；

• 故障攻击：攻击者通过注入故障（如电压干扰）使服务器生成错误签名，需强制验证m' = RSAVP1(pk, s)（BlindSign 步骤 3），确保签名正确性 [FAULTS]。

6.2 消息熵与低熵风险

若客户端使用PrepareIdentity处理低熵消息（如用户手机号），恶意服务器可构造无效公钥（如n为合数但非两个大素数乘积），通过观察 “签名是否成功” 推断消息内容 [Lys22]。解决方案：

• 低熵消息必须使用PrepareRandomize，通过 32 字节随机前缀确保input_msg高熵；

• 客户端可要求服务器提供公钥的零知识证明（如 [GRSB19]），验证公钥合法性。

6.3 随机性安全

协议中所有随机值（r、msg_prefix、PSS 盐）必须通过密码学安全随机数生成器（CSPRNG，如 RFC 4086）生成，禁止客户端直接提供这些值 —— 否则攻击者可能通过恶意构造的随机值注入额外信息（如客户端 IP）。

6.4 后量子安全

当前协议基于 RSA 的 “大数分解难题”，而 Shor 算法可在量子计算机上多项式时间内破解该难题，因此 RFC 9474 明确 “协议不具备后量子就绪性”。未来需结合后量子算法（如格基密码）设计盲签名方案。

7. 典型应用场景

RSA 盲签名的 “隐私保护 + 公开可验证” 特性使其在多个领域落地：

• 隐私支付：Chaum 原始场景，用户生成盲化交易信息，银行签名后解盲，确保交易不可追踪；

• Apple Private Relay：用户通过盲签名证明身份，中继服务器无法关联用户与访问内容 [ApplePrivateRelay]；

• Privacy Pass：替代验证码，用户向服务器请求盲签名，验证时仅需提供签名，避免 IP 追踪 [PRIVACY-PASS]；

• VPN 身份验证：Google VPN 使用盲签名，用户无需暴露真实身份即可完成认证 [GoogleVPN]；

• P2P 通信隐私：Pretty Good Phone Privacy（PGPP）通过盲签名验证节点身份，保护通信隐私 [PrettyGoodPhonePrivacy]。

8. 总结与展望

RFC 9474 的核心价值在于：

1. 标准化：首次规范了基于 RSA-PSS 的盲签名协议，解决不同实现兼容性问题；
2. 实用性：最终签名可通过标准 RSA-PSS 库验证，降低开发与部署成本；
3. 安全性：通过变体设计、错误处理和安全考量，覆盖多数隐私保护场景。

未来需关注两大方向：一是后量子盲签名的标准化（如结合 ML-KEM），二是轻量级变体的优化（如适用于物联网设备的短密钥长度方案）。对于工程实现者，需严格遵循密钥隔离、随机熵注入和侧信道防护原则，确保协议在隐私保护场景下的安全性。