基于辅助谐振的ZVT升压变换器

采用辅助谐振电路的ZVT谐振升压变换器的分析与设计

摘要

本文提出了一种新的零电压转换（ZVT）谐振升压变换器。传统升压变换器在开关导通和关断时会产生开关损耗，这些损耗导致整个系统效率降低。所提出的ZVT谐振升压变换器采用软开关方法，利用包含谐振电感、电容和两个辅助开关的辅助电路，从而比传统硬开关变换器更有效地减少开关损耗。此外，通过使用改进电路，缩短了谐振电感电流的导通周期。实验中，该变换器将电压从200 V升至380 V，开关频率和输出功率分别为30千赫兹和4千瓦。实验结果与仿真结果一致，验证了所提出的变换器的有效性。通过对两种变换器在相同条件下的实验结果进行比较，分析了传统变换器和提出的变换器。实验确认所有开关均实现了软开关，并通过测量两种变换器的效率，证实所提出的变换器优于传统变换器。

关键词

零电压转换；升压转换器；软开关；辅助谐振电路；零电压开关；零电流开关

引言

近年来，由于快速工业化导致的环境和空气污染，引发了环境破坏、气候变化以及极端天气趋势等问题，因此人们越来越关注使用可再生能源来替代化石燃料以解决这些问题[1,2]。

各种潜在的替代能源，包括太阳能、风能、潮汐能和氢能，已成为深入研究的对象。使用燃料电池和光伏太阳能电池的一个缺点是它们的效率非常低。因此，提高电力转换系统的效率非常重要。为此，已开展了大量研究以提高直流‐直流变换器的效率[3–5]。

在设计具有紧凑型[6–8]的直流‐直流变换器时，需要高开关频率。硬开关变换器中的非理想开关元件在开关过程中因电压和电流重叠而产生开关损耗，且开关频率越高，开关损耗越大。这些损耗可通过采用软开关技术来降低。目前已发表大量关于采用零电压开关（ZVS）和零电流开关（ZCS）技术的软开关谐振直流‐直流变换器的研究论文，并提出了多种降低开关损耗的技术[9,10]。零电流转换（ZCT）变换器可通过辅助电路实现ZCS，其谐振条件不受负载变化的影响[11]。但ZCT关断期间由于反向恢复电流会产生开关损耗。电流应力

主开关的导通损耗增加，因为通过谐振电感的部分电流流经主开关。零电压转换（ZVT）转换器具有优势，通过使用辅助电路可在宽负载范围内实现零电压开关和零电流开关。

ZVT转换器使用谐振电感和电容来满足零电压转换条件。由于谐振能量对输出没有显著影响，通过谐振电感的电流为无功电流；同时，由于谐振电流与无功电流相同，谐振电感中的电流较大。因此，高谐振电流会增加无源和有源器件的损耗，并降低整体系统效率。

在传统变换器中，谐振电感电流持续流过辅助电路。因此，所提出的ZVT升压转换器采用改进的谐振电路以降低导通损耗。

本文提出了一种采用辅助谐振电路的谐振ZVT升压DC‐DC变换器，以降低开关损耗并提高变换器效率。该谐振电路由谐振电感、谐振电容和辅助开关组成。该变换器中的辅助电路用于实现软开关方法。通过谐振电路，辅助电路中的开关也实现了软开关方法。此外，采用改进电路减少了谐振电感的导通周期。与相同频率下的传统变换器相比，这降低了开关损耗，并提高了整体系统效率。

2. 谐振升压DC–DC转换器

2.1. ZVT谐振升压变换器

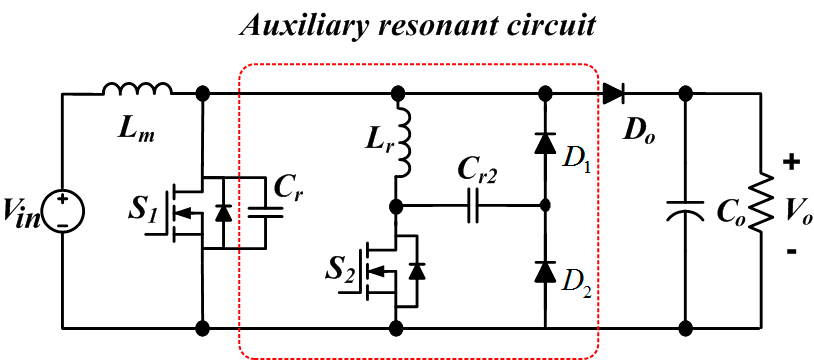
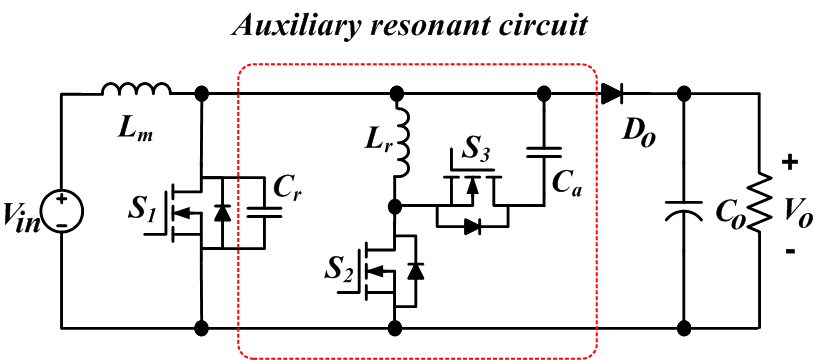
图1a显示了一个传统谐振ZVT升压变换器。其辅助电路由一个升压变换器、一个辅助开关、一个谐振电感、两个谐振电容和两个二极管组成。在电流流过体二极管之前，谐振电容已被放电。这些谐振元件通过谐振电路[15]为主开关在零电压转换下实现软开关构建了一条部分谐振路径。然而，谐振电感电流的续流周期导致了二极管和谐振电感的导通损耗，从而降低了整个系统的效率。

图1b展示了所提出的谐振ZVT升压变换器。该转换器由一个升压变换器、一个主电感、两个辅助开关、一个谐振电容以及带有辅助电容的辅助电路组成。通过使用改进电路，减少了谐振电感的导通周期，从而降低了开关损耗，并提高了整个系统的efficiency。

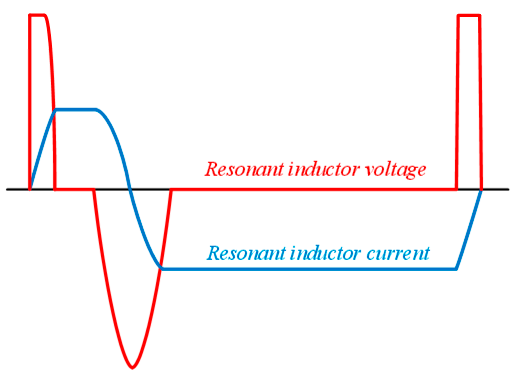
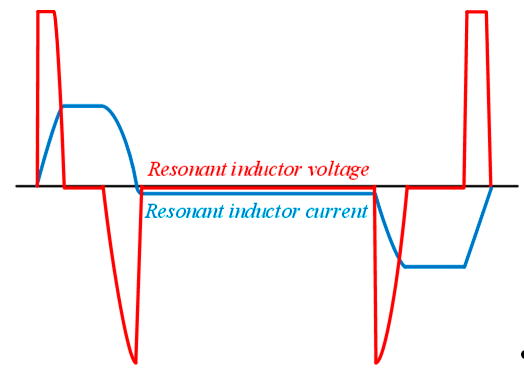
图2显示了谐振电感电压和电流的各个波形 传统转换器和提出的转换器。提出的转换器的电流传导周期 如图2b所示的比图2a所示的传统转换器更短。

2.2. 所提转换器的分析

提出的ZVT谐振升压转换器的工作模式如图3所示。所提出的转换器的工作原理分为十种模式以进行简单分析。模式1、模式2和模式10为所提出的ZVT升压转换器的放电模式。模式4用于满足主开关S1的零电压转换条件。随后，模式5在零电压开关条件下导通。主电感从模式5到模式9处于充电状态。模式3、模式5、模式7和模式9工作在谐振状态。模式2、模式5和模式7为软开通

辅助开关的开关操作。

以下陈述是针对所提出的转换器进行简单分析的假设：首先， 所有开关器件和无源元件（电感和电容）均为理想元件。其次，输入 输入电压200V和输出电压380V保持恒定。第三，所有二极管的恢复时间被 忽略不计。谐振ZVT升压变换器工作在10种不同模式下，以下 假设用于稳态分析：

模式1（t0–t1）：

主S1和辅助开关S2以及S3关断。off。积累的主电感电流Lm流经输出二极管 Do。然后，输出电容和谐振电容CoCr被充电至相同电压。模式1的等效电路和关键波形如图4所示。该 等效电路显示了主电感放电进行升压的过程。

在模式1中，主电感电流iLm减小，谐振电感电流iLr和辅助电容电压vCa为零。这由公式(1)和(2)表示。

$$ iLm(t)= ILm10 − \frac{Vin − Vo}{Lm}(t0 − t1) $$ (1)

$$ iLr(t)= 0, vCr(t)= Vo, vCa(t)= 0 $$ (2)

此外，主电感电流ILm1为下一模式t2的分析定义。

$$ iLm(t1)= ILm1 $$ (3)

模式2（t1< t< t2）：

在模式2中，一个辅助ar ili y开关c2 urns on under the 零电流开关条件。该 it h S t res谐振电感电流iLr 从零开始线性地增加。主电感 电流iLm减小。

当谐振电感电流电感电流iLm时，进入模式2 ent iLr is equal to the mai 完成。此外，图5显示了用于分析模式2的波形。

等效电路和关键w And 等效电路表示主电感的电流iLm和 calculate the magnitude of th 谐振电感iLr。因此，主电感电流达到最小值。主电感 电流iLm 和谐振电感电流iLr 由公式(4)和(5)表示。

$$ iLm(t)= ILm1 − \frac{Vo − Vin}{Lm}t, iLr(t)= \frac{Vo}{Lr}t $$ (4)

$$ iLm(t2) = iLr(t2) ≈ Imin $$ (5)

谐振电容电压vCr等于输出电压。如果忽略谐振开关S3的寄生电容，则辅助电容电压vCa为零。

$$ vCr(t)= Vo, vCa(t)= 0 $$ (6)

对于模式3，谐振电感电流ILr2定义为公式(7)。

$$ iLr(t2)= \frac{Vo}{Lr}t= ILr2= ILm2 $$ (7)

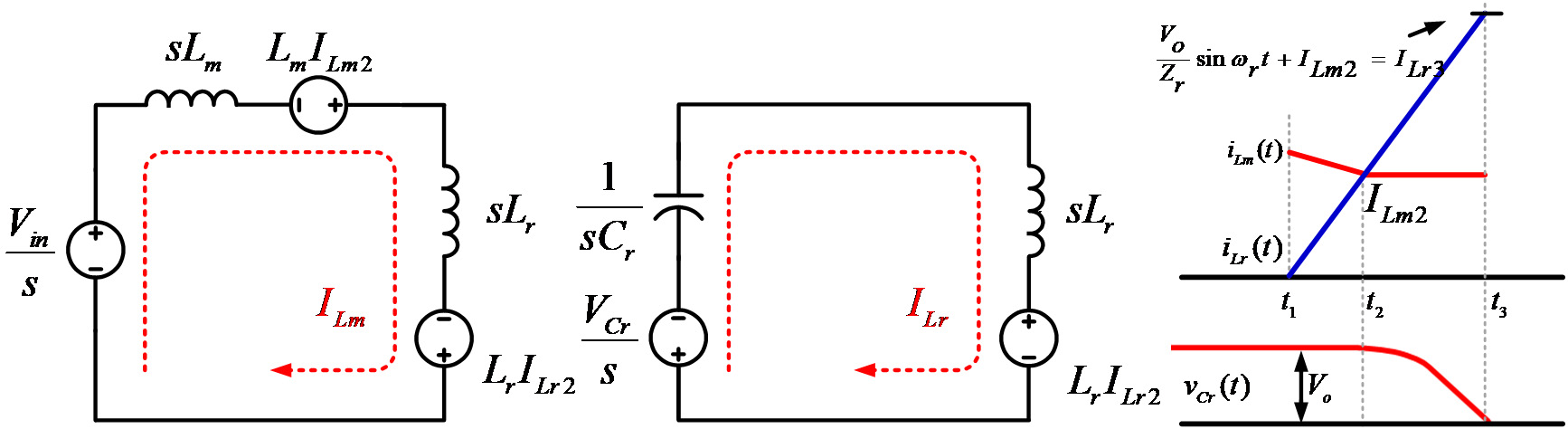
模式3（t2< t< t3）：

当主电感和谐振电感电流iLm和iLr相等时，谐振电容Cr与谐振电感Lr之间的谐振操作开始。随后，由于谐振电容Cr放电，输出二极管Do关断。然后，谐振操作的等效电路如图6所示。模式3的关键波形表明主电感 电流iLm，谐振电感电流iLr 和电容电压vCr。d resonant cap 在模式3结束时，谐振电容的电流变为零。谐振电容电压 pacitor Cr is eq age vCr 和谐振电感电流i ce变换，遵循以下公式 Lr can be obtained by the Lapla (9)、(10)、(12)和(13)。此外，角频率ωr为 n, the resonant impedance Zr an ven

由公式(16)得出。此外，iLm 式(8)、(11)、(14)和(15)。 , iLr, vCa, and vCr are defined by Eq

$$ iLm(t) ≈ Imin $$ (8)

$$ \frac{Vo}{s} = iLr(s)sCr + sLriLr(s)+ Imin $$ (9)

$$ iLr(s)= \frac{Vo Lr √LrCr · 1}{√LrCr s^2+( \frac{1}{√LrCr})^2} + Imin $$ (10)

$$ iLr(t)= \frac{Vo}{Zr} sinωrt+ Imin $$ (11)

$$ CrVo= sCrvcr(s)+ \frac{vLCr(s)}{sLr} $$ (12)

$$ vCr(s)= \frac{1}{sC r + \frac{1}{sL r}} CrVo = \frac{s}{s^2+(\frac{1}{√LrCr})^2} Vo $$ (13)

$$ vCr(t)= Vocosωrt $$ (14)

$$ vCa(t)= 0 $$ (15)

其中

$$ ωr= \frac{1}{√LrCr} , Zr= √\frac{Lr}{Cr} $$ (16)

谐振电感电流ILr3 为下一模式t4 的分析定义。

$$ iLr(t3)= \frac{Vo}{Zr} sinωrt+ ILr2= ILr3 $$ (17)

模式4（t3< t< t4）：

主开关S1的体二极管导通，主开关S1的电压为零。随后，主开关S1满足零电压转换条件。谐振电流流过主开关S1的反并联二极管。主电感电流iLm和谐振电感电流iLr可由公式(18)推导得出。根据公式(19)，辅助电容和谐振电容电压vCr均为零。因此，图7给出了方程的推导过程。开关的电压和电流在关键波形中显示。当辅助开关S2关断时，ff模式4结束。

$$ iLm(t)= \frac{Vin}{Lm}t+ Imin, iLr(t)= ILr3 $$ (18)

$$ vCr(t)= 0, vCa(t)= 0 $$ (19)

主电感电流 ILm4为下一模式t5分析定义。

$$ iLm(t4)= \frac{Vin}{Lm}t+ iLm3= ILm4 $$ (20)

模式5（t4< t< t5）：

在模式5中，主开关S1在零电压开关条件下导通。然后，主电感电流iLm线性地增加。辅助开关S2在同一条件下关断，同时由谐振电感Lr和辅助电容Ca开始第二次谐振。因此，谐振电感电流iLr减小。辅助电容电压vCa和谐振电感电流iLr可通过拉普拉斯变换推导得出，见公式(22)、(4)和(25)。此时，模式5的等效电路如图8所示。该等效电路分为主电感电流iLm和谐振电路。关键波形包括谐振电感电流iLr、主电感电流iLm以及辅助电容电压vCa。

此外，谐振阻抗Za和角频率 ωa由公式(27)给出。然后，iLm、iLr、vca和vCr由公式(21)、(23)和(26)定义。

$$ iLm(t)= \frac{Vin}{Lm}t+ ILm4 $$ (21)

$$ iLr(s)= \frac{LrILr4}{1} \frac{1}{sCa+sLr} = \frac{s}{s^2+(\frac{1}{√LrCr})^2} ILr4 $$ (22)

$$ iLr(t)= ILr4cosωat $$ (23)

$$ ILr4 s= − \frac{vCa}{sLr} + vCasCa $$ (24)

$$ vCa(s)= − √\frac{Lr}{Ca} · \frac{1}{√LrCa} \frac{1}{s^2+(\frac{1}{√LrCa})^2} ILr4 $$ (25)

$$ vCa(t)= −ZaILr4sinωat $$ (26)

其中

$$ ωa= \frac{1}{√LrCa} Za= √\frac{Lr}{Ca} $$ (27)

对于模式6，谐振电感电流iLr 和辅助电容电压vCa 定义为方程（28）。

$$ iLr(t5)= 0= ILr5, vCa(t5) ≈ Vo $$ (28)

模式6（t5< t< t6）：

在模式6中，谐振电感Lr和辅助电容Ca结束第二次谐振操作，谐振电容Ca被充电。主电感电流iLm通过主开关S1线性地增加。当辅助开关S3导通时，模式6结束。模式6的等效电路和关键波形如图9所示。可通过等效电路计算主电感电流iLm。iLm、iLr、vCa和vCr的值如公式(29)和(30)所示：

$$ iLm(t)= \frac{Vin}{Lm}t+ ILm5, iLr(t)= 0 $$ (29)

$$ vCa(t)= −Vo, vCr(t)= 0 $$ (30)

模式7（t6< t< t7）：

在模式7开始时，第三次谐振开始。随后，辅助开关S3在零电流开关条件下导通。谐振电容Cr中存储的能量通过辅助开关S3转移到谐振电感。辅助电容电压vCa和谐振电感电流iLr可通过拉普拉斯变换推导得出，如公式(32)、(33)、(35)和(36)所示。此时的等效电路如图10所示。当辅助电容Ca的电压达到0伏特时，模式7结束，如公式(38)所示。流过主电感Lm的电流线性增加，如公式(31)所示，能量通过辅助开关S3存储在谐振电感Lr中。iLr和vca的值由公式(34)和(37)定义。

$$ iLm(t)= \frac{Vin}{Lm}t+ ILm6 $$ (31)

$$ − ZaILr4 = \frac{iLr(s)}{sCa} + sLriLr(s) $$ (32)

$$ iLr(s)= − \frac{ZaILr4}{Lr} · √LrCa · \frac{1}{√LrCa} \frac{1}{s^2+(\frac{1}{√LrCa})^2} $$ (33)

$$ iLr(t)= −ILr4sinωat $$ (34)

$$ − CaZaILr4= vCa(s)sCa+ \frac{vCa(s)}{sLr} $$ (35)

$$ vCa(s)= − \frac{s}{s^2+(\frac{1}{√LrCa})^2} ZaILr4 $$ (36)

$$ vCa(t)= −ZaILr4cosωat $$ (37)

$$ vCr(t)= 0 $$ (38)

模式8（t7< t< t8）：

在模式8中，辅助电容电压vCa变为零。然后，主电感电流iLm线性地增加，且辅助开关S2的体二极管导通。谐振电感Lr的电流流经体二极管—主开关S1的续流路径。当主开关S1关断时，模式8结束。在此区间内，谐振电感电流iLr的幅值与模式3相同，但电流方向相反。iLm、iLr、vCa和vCr的值如公式(39)和(40)所示：

$$ iLm(t)= ILm7+ \frac{Vin}{L} t, iLr(t8) = iLr7 $$ (39)

$$ vCa(t)= 0, vCr(t)= 0 $$ (40)

模式8的等效电路和关键波形如图11所示。该等效电路分为主电感电流iLm和谐振电感电流iLr。

关键波形表示iLm、iLr、vCa和vCr.

模式9（t7< t< t8）：

在模式9中，主开关S1关断。然后，谐振电感Lr的电流从最大值点减小，同时主电感和谐振电感的总电流对谐振电容Cr 充电。随后，谐振电容的换推导得出，见公式(44)、(45)、(47)和(48)。公式(43)、(46)、(49)和(50)中的iLm、iLr、vCa和vCr值 如下所示：

$$ iLm(t)= ILm8 $$ (43)

$$ −Lr(ILr8) = \frac{iLr(s)}{sCr} + iLr(s)sLr $$ (44)

$$ iLr(s) = − \frac{s}{s^2+(\frac{1}{√Lr C r})^2}(IL8) $$ (45)

$$ iLr(t)= IL8cosωrt $$ (46)

$$ IL8 s = \frac{vCr(s)}{sLr} + vCr(s)sCr $$ (47)

$$ vCr(s)= √\frac{Clrr}{·} \frac{1}{√LrCr} \frac{1}{s^2+(\frac{1}{√LrCr})^2}(IL8) $$ (48)

$$ vCr(t)= ZrILr8sinωrt $$ (49)

$$ vCa(t)= 0 $$ (50)

模式9在图12中分为两个等效电路。然后，展示了谐振操作的等效电路。模式9的关键波形显示了iLm、iLr、vCa和vCr。图12的关键波形显示了主电感电流iLm的最大值。

对于模式10，主电感电流ILm9 定义如下：

$$ iLm(t9)= ILm8= ILm9 $$ (51)

模式10（t 9 < t< t 10 ）：

谐振电感电流i Lr 线性地减小至零。如果谐振电容电压v Ca 被充电至高于输出电压V o 的值，则输出二极管Do 导通。模式10结束，下一个开关周期开始。

模式10在图13中被分为两个等效电路。然后，显示了主电感Lm的等效电路。另一个等效电路表示谐振电感Lr。图13的关键波形显示了主电感电流iLm的最大值。并且谐振电容Cr 被充电至输出电压。

$$ iLm(t) = ILm9 − \frac{Vo − Vin}{L} t $$ (52)

$$ iLr(t)= ILr9 − \frac{Vo}{Lr} t $$ (53)

$$ vCr(t)= Vo, vCa(t)= 0 $$ (54)

2.3. PWM信号分析

主开关和辅助开关的PWM信号如图14所示。辅助开关S2在主开关S1导通之前导通。随后，辅助开关S2的导通区间可分为模式2、模式3和模式4。主开关S1在开通和关断时实现升压。辅助开关S3用于减小导通损耗。辅助开关S3的导通区间可表示为模式7。

所提出的谐振ZVT升压变换器设计由三个开关组成，为实现零电压开关（ZVS）和零电流开关（ZCS），必须满足最小开通和关断时间。主开关控制升压比，其他辅助开关使主开关能够实现软开关。当辅助开关S2导通时，谐振电感Lr和谐振电容Cr的谐振开始。当谐振电容中的充电能量完全放电后，主开关S1在零电压开关条件下导通。在主开关S1导通之前，辅助开关S2已导通并关断。为实现ZVS，需要一定的辅助开关脉宽调制（PWM）最小时间。该时间由模式2、模式3和模式4决定。T2, T3,和T4时间必须满足以下方程：

$$ T2= \frac{−ILm.1LmLr}{VinLr − Vo(Lm+ Lr)} $$ (55)

$$ T3= \frac{sin−1(sin ωrt)}{2πFr} $$ (56)

$$ Fr= \frac{1}{2π √LrCr} $$ (57)

T4通过使用开关元件的时间延迟的系数k来确定。

$$ T4= t× k $$ (58)

$$ t< \frac{Lm(ILr3 −ILm3)}{Vin} $$ (59)

辅助开关S2 的开通和关断时间可以满足以下公式（60）：

$$ TS2> T2+ T3+ T4 $$ (60)

在主开关关断之前，辅助开关S3先导通后关断。当谐振电感Lr的能量释放完毕并达到零之后，辅助开关S3导通。该辅助开关S3在零电流开关条件下导通。在辅助电容Ca放电结束后，辅助开关S3在零电压开关条件下关断。辅助开关S3的导通和关断时间可通过模式7和模式8的公式进行计算。T7所需时间应大于次级谐振辅助频率半周期，而T8所需时间应大于器件的关断延迟时间，后者可从制造商数据手册中获得。辅助开关S3的最短时间应满足以下公式(61)–(63)的要求。

$$ T7= \frac{Tr}{2}= π √LrCa $$ (61)

$$ T8> td(of f) $$ (62)

$$ TS3> T7+ T8 $$ (63)

2.4. 谐振器件设计

谐振电容Cr影响主开关S1的零电压开关操作。当谐振电容Cr被充分充电时，可实现零电压开关过程[16]。因此，谐振电容Cr的设计非常重要。在模式3和模式9中对谐振电容Cr进行充放电时，谐振电感Lr与谐振电容Cr之间的谐振时间可用以下公式表示：

$$ Tmode3= \frac{π}{2} √LrCr $$ (64)

在模式9下，谐振电容Cr 被充电至输出电压，可表示为以下方程：

$$ Tmode9= \frac{Cr Vo}{2Iin_max} $$ (65)

假设谐振电感的最大电流为Iin max，两个电感电流之和为谐振电容Cr的充电电流。当模式9比模式3更长时，缺陷占空比更低。因此，选择时间为0.1 Ts。模式3和模式9的总时间被选为一个周期的1/10。为了实现主开关的零电压开关，谐振电容Cr的充电时间必须更长。因此，谐振电容Cr的值应选择为主输出开关电容的15倍。根据主开关S1,的输出电容，谐振电容的合适值为0.6 nF。主开关S1的输出电容在制造商数据手册中给出。因此，谐振电容Cr选用10 nF以考虑误差裕度。

$$ \frac{π}{2} √ LrCr+ \frac{Cr Vo}{2Iin_max} ≤ 0.1Ts $$ (66)

此外，谐振电感Lr和谐振电容Cr之间的谐振电流对辅助电容Ca充电。模式5和模式7中谐振电感Lr与辅助电容Ca之间的谐振时间被设定为总导通时间的五分之一。如果该谐振电容Cr的充电电压过大，可能会产生电压应力。辅助电容量计算为39 nF。考虑到误差裕度，辅助电容采用了40 nF。

谐振电感Lr与电容Cr之间的谐振为主开关实现软开关。随后，主开关S1满足了零电压转换条件。

谐振设计对于满足ZVS、ZCS和ZVT[17]至关重要。但如果谐振电感电流iLr持续线性增加，电感的磁通将达到饱和[18]。因此，必须利用辅助电容Ca防止电感磁通达到饱和。辅助电容Ca由谐振电感的负电流充电。在这种情况下，能量关系可通过辅助

电容Ca 和谐振电感Lr。因此，电感储能等于或大于电容储能。

谐振电容升r必须充电至低于输出电压电压o。各模式下获得的值可用以下公式(67)和(68)[19–21]表示：

$$ \frac{1}{2}LrIL2r_max ≥ \frac{1}{2} CaVo2 $$ (67)

$$ Ca ≤ \frac{LrIL2r_max}{Vo2} $$ (68)

3. 仿真结果

通过计算机仿真验证了新型ZVT升压变换器设计的工作情况。表1列出了仿真中使用元件的设计参数。本文采用POWERSIM公司PSim9.2软件对提出的转换器进行测试。仿真时间步长为1E‐007，以便进行详细的波形分析。表1列出了仿真中使用元件的设计参数。仿真在30kHz开关频率和200– 380V电压下进行。

表1. 所提零电压转换（ZVT）转换器的参数。

参数	符号	值	参数	符号	值
输入电压	Vin	200伏特	主电感	Lm	1 mH
输出电压	Vo	380伏特	谐振电感	Lr	35微亨
额定功率	P	4 kW	谐振电容	Cr	10 nF
开关频率	f s	30千赫	辅助电容	Ca	40 nF

每个PWM信号的波形如图15所示，谐振电感电流iLr根据每个PWM信号流动。

提出的转换器的电流传导周期比传统变换器短。各开关的电压和电流波形如图16所示。每个开关的软开关操作已成功实现，如图16b所示。由于辅助开关之间的谐振，也出现了一些电压振铃现象。S2和S3。仿真中使用的开关为非理想开关，其寄生电容可能导致开关故障。具体而言，输出电容与谐振电感发生谐振，从而引起振铃。这些谐振可能会导致器件上的电流或电压应力增加，最终提高器件的电压额定值。

4. 实验结果

为了验证理论分析，在图18所示的所提出的ZVT升压转换器上进行了实验。该电路由一个升压转换器、一个控制器和一个栅极驱动器组成。本实验中使用的控制器是德州仪器的DSP TMS320F28335。实验采用4 kW、30 kHz变换器进行，将电压从200 V升至380 V。

为了比较传统转换器和提出的转换器，图19展示了主电感和谐振电感的电流波形。当主开关S1导通时，通过主电感Lm的电流线性增加。当主开关S1关断时，存储在主电感Lm中的能量通过输出二极管Do释放，并传输到负载。相同类型的波形如图2所示。观察到传统转换器的导通周期大于提出转换器的导通周期。

主开关S1上的电压和电流波形如图20所示。在主开关S1导通之前，主开关的体二极管处于续流周期。随后，在零电压转换条件下，主开关实现了零电压开关导通。图20显示了电压和电流通过主开关S1的波形。图20b是主开关S1电压和电流软开关过程的放大视图，软开关过程中主开关S1的电压和电流波形。

辅助开关S2上的电压和电流波形如图21所示。由于谐振电感的存在，辅助开关S2在零电流开关条件下导通，因此辅助开关S2的电流从零开始线性增加。辅助开关S2的电压为零，辅助电容Ca不影响辅助开关S2。因此，辅助开关S2的波形由负谐振电感辅助电容和谐振操作决定。图21b显示了软开关扩展辅助开关S2。

图22显示了辅助开关S3两端的电压和电流波形。主开关的体二极管在零电压开关条件下导通。随后，由于谐振电感Lr和辅助电容Ca的作用，辅助开关S3在零电流开关条件（ZCS条件）下导通。之后，辅助开关S3的电压保持为零。图22b展示了辅助开关S3软开关的扩展情况。由于辅助开关S2和S3之间的谐振，产生了电压振铃。仿真中使用的开关为非理想器件，其寄生电容可能导致开关故障。具体而言，输出电容与谐振电感发生谐振，从而引起振铃。

输入/输出电压和电流波形如图23所示。电压从200伏特的输入电压升压至380伏特的输出电压，表明对输出电压的良好控制。

传统(C)转换器与提出的(P)转换器的效率比较如表2所示。使用功率分析仪（型号WT‐3000）验证了提出的转换器的效率。在测量可变负载时，输出功率380伏特和输入功率200伏特保持不变，基于4千瓦的额定容量。根据效率测量结果，确认满载效率超过90%，并在95%负载时测得最大效率为96.5%。

表2. 传统转换器与提出的转换器的效率比较。

Load [%]	Vin [V]	Iin [A]	Vo [V]	Io [A]	Win [W]	Wo [W]	效率 [%] C	效率 [%] P
28%	196.4	6.03	387.5	2.7	1184.29	1046.25	88.34	90.14
55%	200.8	11.27	384.9	5.3	2263.02	2039.97	90.14	92.43
76%	198.7	15.57	386.6	7.32	3093.76	2829.91	91.47	93.94
95%	199.2	19.11	385.1	9.32	3806.71	3589.13	94.48	96.53

5. 结论

本文提出了一种采用辅助谐振电路的谐振ZVT升压DC–DC变换器。所提出的转换器的所有开关均工作在ZVS和ZCS下，因此通过使用谐振电路降低了开关损耗。该转换器由两个开关、一个谐振电感和两个谐振电容组成。此外，与传统变换器相比，所提出的转换器降低了谐振电感的导通损耗。因此，在相同频率下，所提出的转换器比传统变换器具有更高的系统整体效率。为验证其性能，进行了实验。实验测得所提出的转换器的效率为96.5%，相较于传统谐振转换器的94.2%有显著提高。此外，基于数学建模，分析了每种工作模式的等效电路。根据电流和电压波形对工作模式进行了划分。通过仿真验证了所提出的转换器的有效性。综上所述，仿真结果与实验结果一致。因此，所提出的高效率变换器适用于直流配电和传感器系统的光伏变换器等应用。