基于众包轨迹的立交三维制图

使用众包轨迹数据详细绘制立交节点

任畅、唐炉亮、杨雪和杰德·朗

摘要

作为交通地图中的重要组成部分，立体交叉路口的三 维（3D）结构信息对于智能驾驶、路线规划和交通控制等应用 至关重要。为了获取道路交叉口的空间布局，研究人员已开发出 从多种数据源中提取平面结构的算法。然而，利用追踪数据对包 含三维结构信息的立体交叉路口地图进行细化的研究仍较少。本 研究旨在寻找一种从车辆轨迹中提取立体交叉路口三维结构的方 法。提出的方法基于语义分割和数据融合技术。通过检测变点， 将轨迹划分为具有不同高程趋势的路段；然后利用数据融合技术， 在不同轨迹之间寻求共识，从而确定坡度和平直路段的范围及高 程。基于语义分割和聚合高程，我们重构了详细的三维立交节点 结构。该方法在多个众包轨迹数据集上进行了验证，并与聚类中 心连接法进行了比较。实验结果表明，提出的方法在语义分割的 总体精度上高于基线方法；在交叉口处的垂直关系准确性方面与 基线方法相当。尽管不同轨迹之间存在较大的高程差异，提出的 方法在来自开放项目和商业项目的众包轨迹数据集上的表现依然 稳定且相近。

索引术语 —众包追踪数据，立体交叉路口，高精地图，地图 构建，语义分割。

一、引言

MAPS 道路网络对于导航、定位和城市管理[1]–[3]等 各种应用至关重要。近年来，从车辆轨迹构建道路地图的 研究已广泛开展，并涌现出三类方法：点聚类，
稿件于2020年2月21日收到；2020年11月6日和2020年12月18日修 订；2021年1月15日接受。本工作部分由中国国家重点研发计划项目 2016YFE0200400资助；部分由国家自然科学基金项目41971405、项目 41901394和项目41571430资助；部分由中国国家留学基金管理委员会 项目201906270227资助。本文的副编辑为R.马莱基安。（通讯作者： 唐炉亮；杨雪。）任畅和唐炉亮隶属于中国武汉大学测绘遥感信息工程 国家重点实验室，武汉430079，中国（电子邮件：tll@whu.edu.cn）。
杨雪隶属于中国地质大学地理与信息工程学院，武汉430074，中国 （电子邮件：yangxue@cug.edu.cn）。杰德·朗隶属于加拿大安大略 省伦敦市西安大略大学地理与环境系，N6A5C2，加拿大。数字对象标 识符10.1109/TITS.2021.3054910

增量插入和交叉口连接[4]。在现代城市中，复杂立交的 建设日益增多，因为它们能够促进高速公路与道路交叉口 的交通流量[5]–[7]。这对现有的地图构建算法，特别是 交叉口连接方法，提出了挑战，因为复杂立交具有内部结 构，需要比点几何更详细的表示[8],[9]。

通用地图构建算法能够提取具有简单十字路口的道路 网络，但现实中存在多种多样的平面交叉和立体交叉交叉 口[10]–[12]。互通立交中密集且连通性各异的匝道会干 扰点聚类方法中的聚类和骨架提取过程[13]–[15],，导致生 成错误的线性特征。具有高密度匝道的交叉口也会阻碍增 量插入方法中轨迹的正确匹配[16]–[18]。在交叉口连接方 法中，复杂立交可能被识别为多个交叉口或作为一个整体 [19],[20]。多重识别容易引入连通性错误，而整体识别 则忽略了交叉口的详细内部结构。现有算法难以应对几何 与拓扑复杂性，无法生成道路交叉口的详细地图。因此， 亟需专注于绘制复杂立交结构的新地图构建方法。

协作式地图项目提供了开放的地理数据，支持成功的 商业地图服务用于导航[21],定位[22]和可视化[23],， 证明了众包的可行性。航空影像一直是一个重要来源，志 愿者和企业都将精力投入其中[24]–[26], ，而众包全球定 位系统（GPS）轨迹数据尚未被充分利用，作为一种低成 本手段来在变化的世界中保持更新。本文提出一种方法， 利用带有高程信息的众包车辆轨迹数据提取立体交叉路口 （下文简称为交叉口）的结构。我们通过对轨迹数据中的 高程记录进行语义分割，识别道路与匝道中的坡度和平直 路段。该方法基于数据融合中的共识思想，尝试解决众包 轨迹中存在的冲突和不一致性。我们提供了一种理解和利 用车载定位传感器数据的新视角，以及一个使用轨迹数据 详细绘制道路交叉点的实用流程。

二、相关工作

在以往的道路交叉口制图研究中，主要包含三个阶段： 交叉口识别、几何轮廓描述和语义提取。已有多种方法用 于在图像、点云、矢量地形图和车辆跟踪数据中识别交叉 点。这些方法将交叉口定位在一个点或一个区域内，从而 能够基于空间邻近性筛选出与交叉口制图相关的数据点。

在第二阶段，对相关数据进行进一步处理，以获得交 叉口内道路与匝道的线性表示。对于图像或点云，这意味 着需要将代表不同道路结构的像素或点从整个交叉口中分 离出来。由于视觉遮挡和几何复杂性，这些方法仍需借助 地形图等辅助数据来提取复杂立交的三维结构[36]。否则， 仍难以对复杂立交点云中强连接的结构进行分割[37]。对 于地图和追踪数据，当前研究仍主要集中于平面布局 [4],[19]，从轨迹中提取三维道路几何形状的研究较少[38]。

现有方法包括匹配和合并高程序列[39] ，以及直接对三 维轨迹点进行聚类[40]。这些方法受高程测量质量的影响 较大，因此在使用众包数据进行交叉口精确制图时需要格 外谨慎。

语义信息提取也是提升地图在路线应用中可用性的关 键步骤[35],[41]。通常会在平面交叉[35]处提取拓扑连
接性。对于行人和轮椅使用者而言，使用出入口信息[42]
丰富地图数据库中的路径是有帮助的。这两项研究均表明， 语义信息应反映有助于地图用户在现实世界中导航的关系， 从而促使我们对道路结构的相对垂直顺序进行评估。在三 维交叉口方面，John等[43]从带高程的轨迹数据中提取 了街道的坡度值。本研究的基本处理单元是交叉口之间的 道路路段。然而，该粒度仍不足以反映交叉口内部道路坡 度的局部变化，这促使我们将道路/匝道划分为具有坡度 或平地语义标签的路段。

三、方法

在本节中，我们提出了一种利用众包轨迹数据进行道 路交叉口三维测绘的新方法。我们的模型包含三个步骤： 坐标参考系统的统一、高程序列的语义分割以及多车辆观 测结果的融合。其基本思想是将轨迹划分为同质路段，并 对每个路段内的聚合高程序列进行聚合。在此，满足两个 条件的数据点被视为同质且适合聚合：一是代表相同的道 路结构，二是表现出单一高程趋势。第一步通过将具有相 似进出方向的轨迹分组来实现第一个条件；第二步

根据高程序列的趋势，将每组中的轨迹划分为多个部分。
最后一步寻求多条轨迹高程序列之间的共识。

A. 参考系统统一

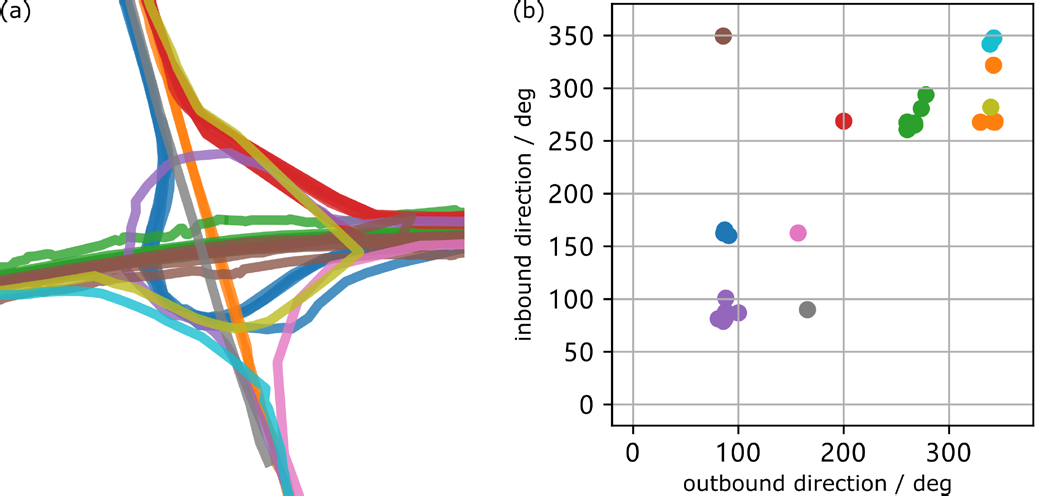
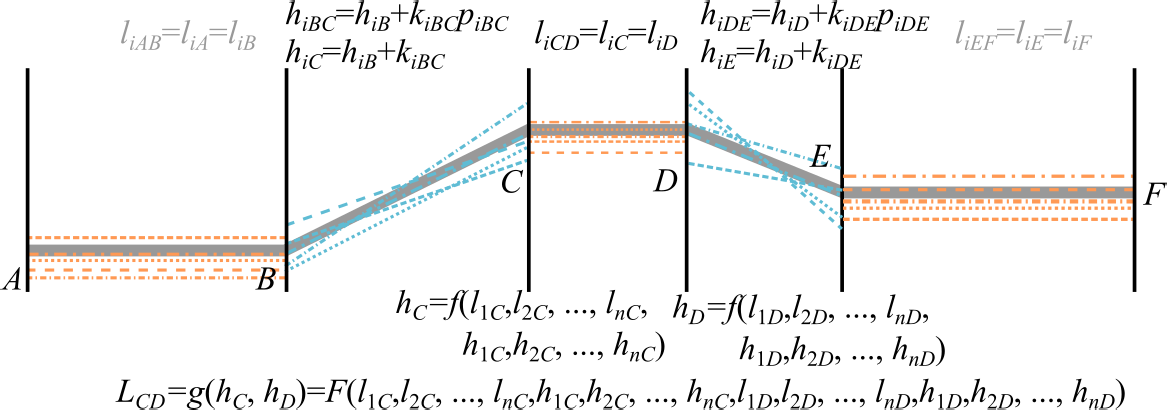
在分离式立交交叉口中，道路结构的几何形状十分复 杂。车辆通过交叉口时，在不同的道路结构上朝各个方向 行驶。将以相同方式通过交叉口的轨迹聚类为转向组。 例如，在图1a中，深蓝色线条表示从北到东的聚类。我们将 每个组的平面形状聚合为水平基准，并通过对齐高程测量 来统一垂直基准。

1) 聚类转向组：

转向组定义为从交叉口具有相似进 出方向的一组轨迹。通过聚类轨迹的方向特征来构建转向 组。对于每条经过交叉口的轨迹，我们计算与其起止位置 点相关联的航向方向。平均值代表该轨迹的进、出方向， 作为其特征。图1b中的散点图展示了轨迹在进（纵轴）和 出（横轴）方向特征空间中的分布情况。由于众包数据集 在不同交叉口的覆盖范围各异，因此需要一种无需预先指 定聚类数量的聚类算法来处理这些轨迹。基于密度的带噪 声应用空间聚类（DBSCAN）适用于将轨迹划分为不同的 转向组。DBSCAN中的邻域准则应考虑方向观测中的误差， 同时具备区分不同道路的能力。阈值设定为45度，因为垂 直交叉道路是交叉口的常见情形。在计算角度差时，方向 应作为循环量进行处理。形成一个聚类所需的最小样本数 设为1，因为每个转向组中的众包轨迹数量可能从零到多 个不等。

2) 二维线性参考：

通常有多条轨迹采样自对应于一个 转向组的相同道路结构（图2a）。它们需要聚合以形成一 条表示几何形状的中心线

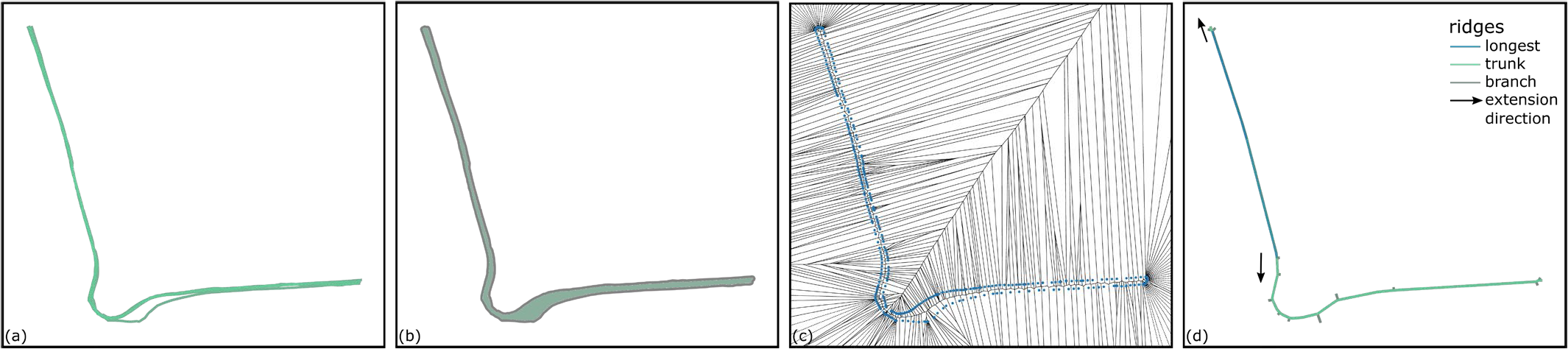原始轨迹(b)缓冲多边形(c)多边形顶点的Voronoi图(d)脊线与主干提取)

在水平维度上的转向组。我们可以通过合并转向组中轨迹 的缓冲区来生成一个粗略轮廓（图2b）。缓冲半径应设置 为定位点的估计水平精度。随后，我们生成缓冲多边形顶 点的Voronoi图（图2c），以从有限脊线中提取多边形的 骨架（图2d）[44]。从最长的脊线开始，我们在两端延伸 该脊线，从而得到一条连续无分支主干作为中心线。

自相交轨迹是上述步骤中的特殊情况。一个常见的例 子是在右侧行驶规则下通过苜蓿叶式立交桥进行左转。解 决方案是在自相交形成的环路的任意位置将其分割。这样， 轨迹被分成两个相交的部分，但每一部分都是简单几何体， 不自相交，适合进行骨架提取操作。

中心线的提取为该组创建了一个线性参考基准，这是 组织和描述来自不同轨迹的路段的基础。在后续的语义分 割和聚合步骤中，所有定位点都将投影到此中心线上。因 此，我们可以使用相对位置来统一且可比较地确定观测到 高程的点以及带有语义标签（例如倾斜或水平）的路段。

3) 调整观测高程：

消费级设备测量的高程存在较大误 差。在提取可靠的地理信息之前，需要对高程测量进行预 处理。在此步骤中，我们考虑了John等[43]所识别的两 类高程误差：一类是与每次观测时段相关的绝对误差，另 一类是特定观测时段内各观测值之间的相对波动。

对于跨时段差异，由不同设备采集的定位点均参考现 有的数字高程模型（DEM）或数字表面模型（DSM）。
轨迹与地形模型之间存在一个相对较大但稳定的偏移[45]。
造成这种差异的原因包括不同设备和记录软件[46],所使 用的不同高程基准，以及在不良条件下卫星定位解算中的 粗差[47]。一种调整方法是为每个时段的地形模型增加一 个估计的中位数差异。这将使所有轨迹对齐到同一高程基 准。调整量设定为轨迹与地形模型之间的中位数差异（1）， 以减轻

来自不同源的测量值之间的冲突
zadj= zobs+ median(zref(xi, yi) −zobs(xi, yi)) (1)
在(1)中，zadj和zobs表示调整后的高程和观测高程，zref
(xi,yi)表示根据参考地形模型得到的第i个位置的实际高程。

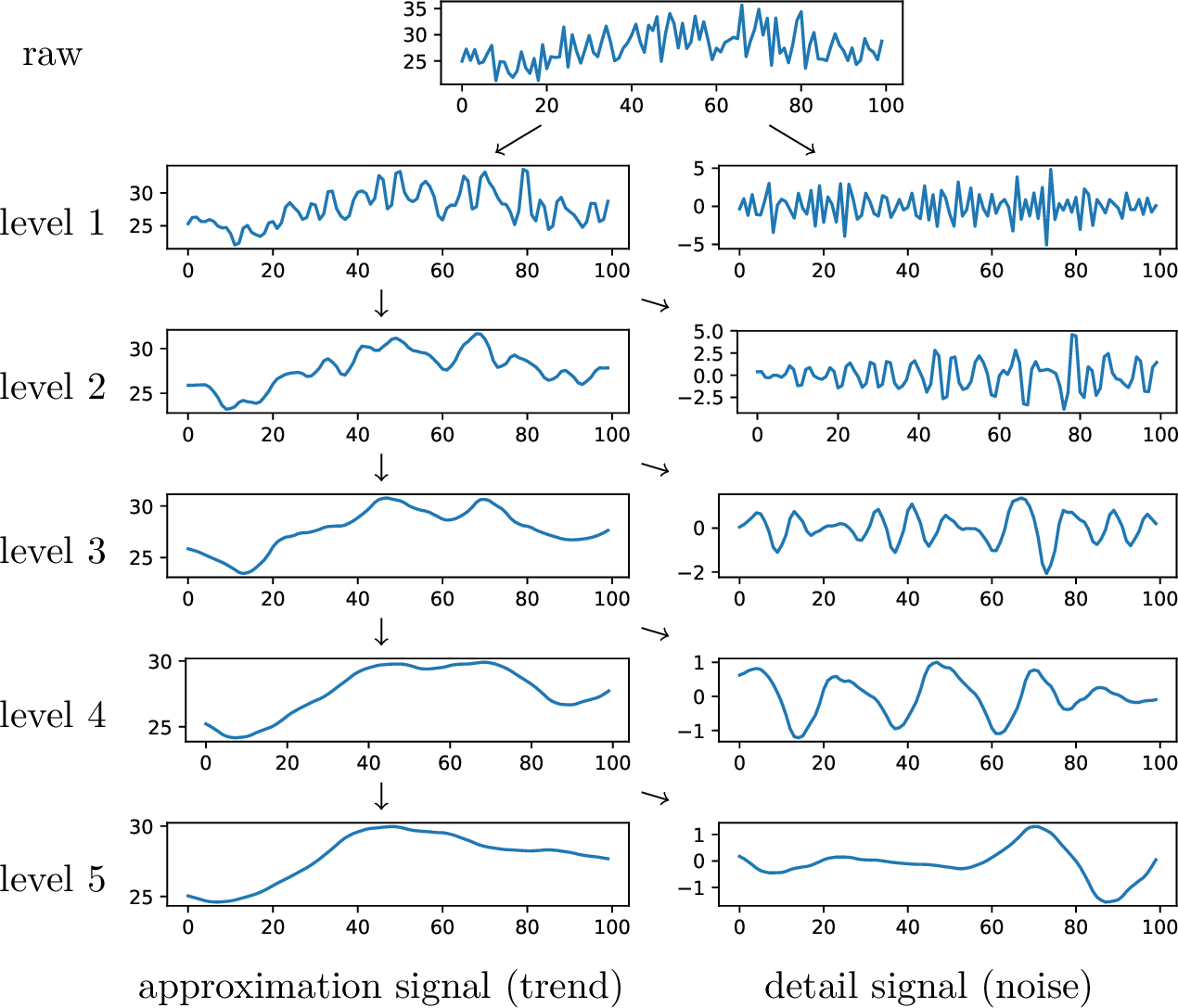
对于系统内的随机误差，离散小波变换（DWT分解） 能够去除高程观测序列中的噪声（图3）。输出的近似分 量代表输入信号的平滑趋势，而细节分量主要包含噪声。
Daubechies4小波适用于识别平地和坡度，因为它能同 时保留连续和突变的变化[48]。DWT分解的第3层近似分 量适合用于去噪目的[49]，本研究采用了该分量。当需要 避免边界效应时，分解水平还取决于信号长度。如果轨迹 点不足以进行第三层分解，则在信号需要填充时停止分解。
因此，DWT的分解水平根据公式(2)确定，其中n为高程 序列的长度，m为小波的有限冲激响应长度。

对于Daubechies4的情况，m= 8。
L= min(3, ceil(log n m −1/ log2)) (2)

B. 高程序列的语义分割

道路网络通常在地图数据库中表示为交叉口之间的路 段。然而，在交叉口中，交叉口并不是定义路段的良好标 准。根据路面的高程趋势将道路与匝道划分为平直路段和 坡段更为合理。分治策略将有助于对轨迹数据中的高程信 息进行分段建模以及对立交节点的精确制图。

从原始轨迹中识别坡度的问题可以抽象为变点检测问 题。该问题的两个关键点是确定变点的数量和位置 [50],[51]。变点检测方法具有不同的能力：能够精确提 取变点位置的方法通常需要预先给定变点数量，而能够自 动确定变点数量的方法则倾向于将一段变化过程识别为单 个变点。因此，有必要结合这两种方法，以更好地检测轨 迹中的坡度（图4）。

1) 粗略变点检测：

在本研究中，我们采用了一种较 为简化的几何模型，该模型虽简单但足以满足交叉口制图 的需求。平直路段是指高程保持不变的道路与匝道，而坡 段则是指高程从一个平地变化到另一个平地的路段。因此， 车辆在路面行驶过程中采集的高程序列可以通过多个均值 之间的变化进行建模。坡段的数量可通过剪枝精确线性时 间（PELT）方法[52]进行确定并粗略定位。该方法将每 个均值的变化过程识别为一个点（图4b），然而我们需要 起始点和结束点来将坡度表示为线性对象。尽管如此，精 确定位坡度范围仍然至关重要，因为粗略变点可将整条轨 迹划分为仅包含一个坡度的路段。

2) 坡度范围精确定位：

对于仅包含一个坡度的高程序列 （ES1S），序列Mann‐Kendall（MK）检验[53] 可进一步提 取坡度段起始点和结束点的精确位置。单次MK检验可以
表明变点的存在。在序列Mann‐Kendall（MK）检验中， 将序列在每一个点处划分为两个子序列，并分别进行 MK检验，以定位序列趋势发生变化的位置。例如，在图 4c和图4d中，蓝色和橙色曲线分别显示了某一给定点之 后（前向）和之前（后向）子序列的检验统计量。水平线 表示检验统计量的临界值。在一个ES1S的前向子序列中， 变点检验结果由显著变为不显著。前向子序列中最后一个 显著的点，表示该点之后的趋势与ES1S尾部趋势不同，即 坡度的终点。类似地，对于一个ES1S的后向子序列，子序 列中第一个不显著的点标志着坡度的起点。通过这种方式， 可以从完整序列中变点的粗略位置进一步细化坡度的范围。
尽管上述过程可以将多条轨迹的高程作为输入，但分别对 每条轨迹单独应用该方法仍然更有利，因为不可靠观测在 与其他数据混合时可能产生负面影响。

C. 多源观测融合

存在潜在差异的结果需要使用能够处理错误观测的鲁 棒数据融合技术，在转向和路段层级进行聚合。语义分割 结果，即坡度范围，针对每个转向组进行聚合，以稳健地 将轨迹划分为坡度段和平直路段。在此基础上，各路段的 高程被拟合为线性模型，并在连续性约束下进行聚合。

1) 线性参考中的坡度范围：

对于单个轨迹，通过 PELT和序列MK方法提取的坡度范围仍受测量不精确的 影响（图5a）。对同一转向组中轨迹的坡度范围进行聚合， 将使语义分割更加稳健。

在统一的线性参考基准中，高程观测值表示为在线上 相对位置的一个标量（图5b）。坡度的范围则表示为相对 位置的二元组，即一维变量的区间观测。布鲁克斯‐艾扬 格尔（BI）算法是一种适用于来自多个源的区间观测的数 据融合技术，可生成稳健的点和区间

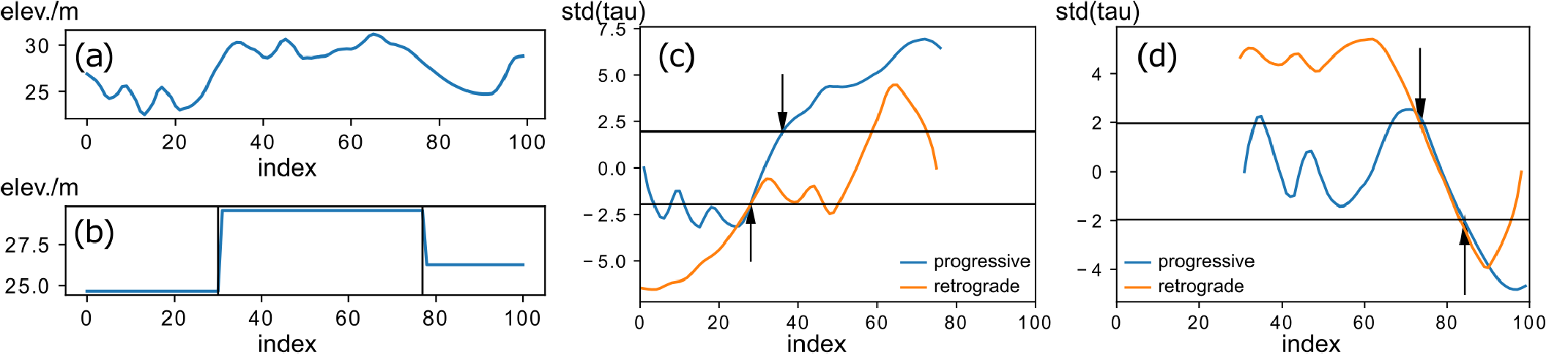在转向组中检测到的多条轨迹（不同 虚线样式）中的坡度范围（蓝色）和平直路段（橙色）（中心线为灰色）。
(b)表示在中心线上相对位置的坡度范围。(c)将某相对位置识别为坡度的轨 迹数量，称为布鲁克斯和艾扬格尔的加权区域图[46]。(d)最终语义分割。)

估计[54]。它适用于同一转向组中存在多个坡度范围的情 况，其中具有足够观测支持的区间是期望的输出。例如， 在加权区域图（图5c）中，至少有四个观测支持的区间最 终被确认为坡度。

基于聚合的坡度范围，其补集（即非坡度的范围）被 标记为平段。每个轨迹点均被匹配到坡度或平段中（图 5d）。这种最终语义分割实现了对来自不同来源的不一致 高程观测值进行分段拟合和建模。

2) 路段高程协调：

语义分割使我们能够将每条原始轨 迹中的高程观测值拟合到合适的模型中。对于平段，其高 程应保持恒定，因此均值可作为一个合理的模型。对于坡 度段，使用线性模型即可充分捕捉在线性参考下相对位置 的高程变化。在图6的示例中，由于有多条轨迹穿过同一 路段，因此每个路段存在多个模型。我们将平段AB的均 值模型表示为liAB，其中i为轨迹的索引。坡度段BC的线 性模型为hiBC，其中截距hiB表示在点B处的高程估计值。
点C处的估计高程为hiB+kiBC，因为点C的线性参考位 置pi在路段BC中为1。这些独立的模型

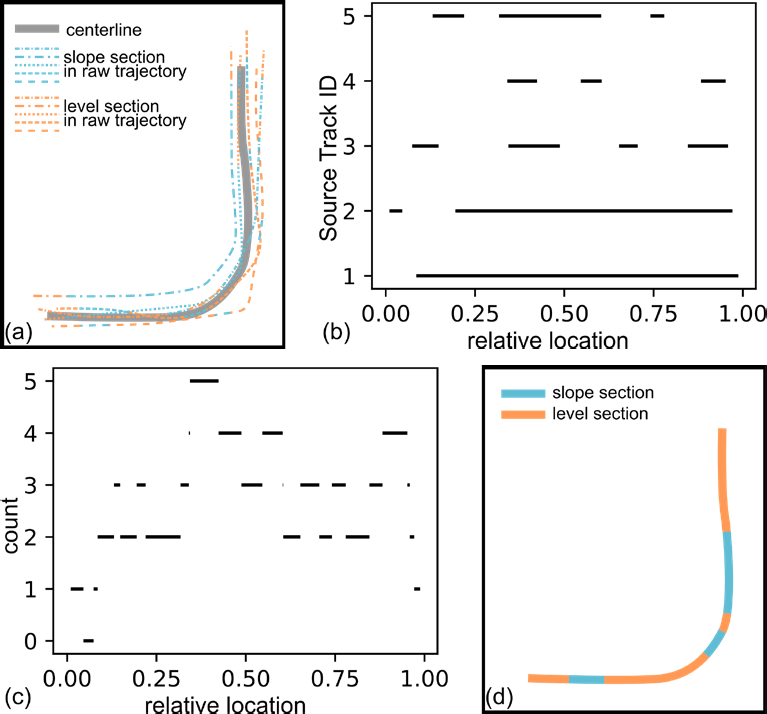
每个转向组都需要进行聚合。由于坡度和平直路段应在两 端相互连接，因此任何聚合都应保持这些点处的高程连续 性。

在此约束下，我们关注平段CD的高程，以确定哪些 观测值与聚合相关。经过路段CD的轨迹是该路段的有效 样本，因此每个样本的平均高程（liCD）被纳入考虑。相 邻路段BC和DE的线性模型也相关，因为这些模型提供了 端点C或D处的高程估计（hiC和hD）。因此，我们可 以利用BI算法[54]，结合两个端点的估计（hC和hD）以 及路段上的估计（liCD），对CD的高程LCD得出共识。
由于BI算法以区间作为输入，我们可以设置显著性水 平 α ，将高程的点估计转换为区间估计，以建模其不确 定性。对于平段，我们基于正态分布定义一个区间Li(α) ， 该正态分布的均值为Li，标准差 σi来自经过该路段的轨 迹i的相关高程样本。对于坡度，线性模型预测在两个端
点处的标准差也可获得，因此可在给定显著性水平 α[55]
下得到预测区间。现在，两类点估计均已转换为区间，我 们便能够应用BI算法的思想来聚合所有相关轨迹的估计结 果。考虑到众包轨迹数据中存在巨大差异，点估计可由中 心间隔的中心点得出，这与原始BI算法中的均值设定略有 不同。

将估算的高程与转弯中心线相应端点关联后，我们最 终得到了立体交叉口道路结构的带注释线性几何表示。该 工作流程如图7所示。

四、实验与分析

A. 实验设置

1) 设计：

我们进行了三组实验，使用合成高程序列和众包轨迹数据集来验证提出的方法。我们的共享数据集包含了第二组和第三组中十五个交叉口的汇编开放数据。在第一组实验中，我们生成了具有可控参数的噪声，以检验噪声如何影响提出的方法识别坡度的能力。

在第二组中，我们使用提出的方法和基线方法，从不同区域的开放数据中提取并评估了十个交叉口的结构。在第三组中，我们从开放数据和商业轨迹中提取了另外五个交叉口，以研究众包中主动与被动数据采集方式的影响。

这些组中提取的交叉口结构通过坡道/平段分割和垂直顺序进行评估，这两项分别对应于提出的方法中的两个关键步骤，即语义分割和数据融合。

我们在GIS软件中交互式地选择了相关轨迹子集作为第二组和第三组的输入数据。该范围应包含与交叉口相连道路的合理延伸，以方便计算进出方向。尽管此过程可以使用第二节中提到的交叉口识别算法实现自动化，但对该区域进行近似选择已足够。

2) 基准数据和基线方法：

为了评估结果，我们从OpenStreetMap获取了交叉口的数字地图，其中一些道路路段标注了层级顺序和坡度属性。基于这些属性不完整的底图，我们还参考了街景图像来准备基准数据。对于坡道/平段语义，我们为每个转向组补充了底图中缺失的坡段。对于垂直顺序信息，由于交叉口设计和轨迹数据覆盖范围的不同，并非所有转向组都在分离式等级上相互交叉。

我们检查了若将结构投影到地面平面上时哪些结构会相互交叉，然后标注了一个结构位于另一个结构之上还是之下。

与基准结果的比较揭示了所提出方法的性能，同时也需要与其他方法的性能进行对比。由于目前缺乏广泛接受的方法来完成此任务，因此选择一种经典且简单的基线方法作为通用参考，以便其他研究人员更好地理解和轻松比较。因此，我们首先选择使用一种经典方法构建二维地图，该方法基于欧氏距离利用k‐均值算法对跟踪点进行聚类，并连接各聚类中心。然后将每个聚类中心的高程设为该聚类内点的平均高程。在基线方法中，根据道路设计标准，当倾斜度大于5%阈值时，将其标记为坡度。

3) 性能指标：

语义分割过程将道路和匝道分类为坡度或平地段落。我们将所有提取的坡度和平地段转换为相对于底图的线性参考范围后，分别计算了坡度和平地段的F分数指标。检测到的坡度范围与基准中标注的坡度相重合的总相对长度被视为坡度真阳性（TPS）。坡度假阳性（FPS）指在基准中为平地段但被识别为坡度的部分。底图中的非坡度范围如果被检测为平地段，则视为坡度真阴性（TNS）。对于平地段的定义类似，例如平地段真阳性（TPL）等同于TNS。除了针对每种类型的上述度量外，我们将正确检测到的坡度和平地段的相对长度之和，即 TPS+TPL，定义为整体语义准确率。

每个交叉口的垂直顺序均与真实值进行了核对，因为这对地图使用者提供了关键指引。我们定义了一个简单的垂直顺序正确率指标，即正确配对的数量与排除不相交转向后的总配对数量之比。

B. 合成示例

1) 合成数据的生成：

该模拟基于一条由两个坡度和三个平直路段组成的合成道路，该道路在100个采样点上进行采样。平段高程分别为25米、30米和26米，坡度连接这些平段。坡度分别位于第20至40个和第70至85个采样点处。向该理想数据集添加了具有自相关[56],[57]的高斯噪声，作为输入高程序列。

我们控制标准差为3米，并针对自相关水平 ϕ=0.4、0.6、0.8，分别生成了100个噪声序列。通过将每个噪声序列添加到理想数据集中，合成了300组含噪高程观测值，以检验自相关对坡度提取的影响。该过程还重复应用于其他噪声强度水平（标准差 σ=1米、5米），得到了另外600组数据，以检验噪声强度对坡度提取的影响。

2) 结果：

将前300组带有噪声的高程数据输入到提出的语义分割算法中，并采用不同显著性水平参数（p= 0.01、0.05、0.1）进行序列MK检验。结果的描述性指标如图8所示。可以看出，提出的方法在检测到的坡度数量和坡道检测精度方面对显著性水平参数不敏感。然而，随着 p值增大，检测到的坡道长度和召回率有所下降。噪声中的自相关对性能影响有限，但当自相关高达0.8时，会导致明显的坡度误识别。

所有900条合成高程序列均通过所提出的语义分割算法在典型显著性水平p= 0.05下进行处理。从图9可以看出，噪声强度增加对提出的方法的坡度检测能力主要表现为精度下降。坡度的召回率下降程度不如精度显著，表明高强度噪声更容易导致坡度的误检，而非对已有坡度的漏检。当噪声强度较低时，检测到的坡度数量较多，但坡度长度并未增加，表明检测到的坡道被分割为多个段落。

C. 不同区域的性能

1) 数据：

除了地图数据外，OpenStreetMap还托管了由志愿者主动收集并上传用于协同绘图的轨迹数据。从该平台获取了上海市和武汉市的行程数据，并根据不同的数据覆盖范围（表I），选取了十个不同类型交叉口进行实验。

2) 结果：

提出的方法在大多数交叉点的整体语义准确率超过70%，而基线方法在超过一半的交叉点处的性能低于该值（表二）。两种方法在相对垂直顺序上的平均准确率相似。提出的方法能够利用多条轨迹来定位交叉口的坡度，每个转向组（BE、BD、CX、JY）拥有更多的追踪数据。当可用轨迹数量有限时（QL、WH、YY），所提出的方法在坡度检测性能方面与基线方法相似。

两种方法在坡度上的F值表现相似，但提出的方法在平段上的F值高于基线方法，这表明在相似结果背后坡度检测策略存在差异。提出的方法在坡度检测中采用了保守策略，仅识别可通过多条轨迹确认的坡度，这种策略可能更适合道路结构的绘制，因为在实际道路与匝道中，坡度通常比平直路段少见。该保守策略的代价是可能遗漏部分坡度，但由于道路与匝道中坡度本身较为稀少，这种遗漏是可以接受的。这也解释了即使较短的坡度未被正确检测，交叉点的总体精度仍然较高的原因。

D. 不同数据源的性能

1) 数据：

众包也可能发生在商业应用中。用户在使用基于位置的服务时，会为商业平台被动地生成大量地理空间数据。此类数据集的质量可能与开放集体地图项目不同，在后者中，志愿者通常会主动尝试更有利于数据采集的条件。我们选择了北京的五个交叉口（表III）进行实验，在这些地点可以获取OpenStreetMap轨迹以及来自科技公司腾讯的用户生成轨迹，腾讯拥有数亿用户。

2) 结果：

商业数据能够在平均整体语义准确率保持在70%以上的同时，将覆盖范围扩展到更多的转弯处，尽管扩展的覆盖范围并未提高坡度的F值以及相对垂直顺序的平均准确率（表IV）。坡度的F值较低以及相对垂直顺序的准确率较低表明，使用所提出的方案更难达成共识或腾讯数据集中的基线方法，这意味着大型数据集在带来更好覆盖范围的同时也引入了冲突信息。

五、结论

本文提出并测试了一种利用众包轨迹数据进行交叉口制图的方法。该提出的方法对单个轨迹的高程序列进行语义分割，随后融合多源估计的坡度范围和高程信息。该方法是一种有效且可行的详细道路结构制图途径，扩展了通用方法在复杂立交中的可用性和适用性。

基于PELT和序列MK检验的高程序列语义分割为道路网络建模提供了子段单元，提高了高程语义的空间分辨率。DWT去噪和BI数据融合的应用能够处理众包轨迹数据中的不一致性和差异。

转向组只是用于聚类相关轨迹和支持导航应用的一个便捷选择，但需要改进以提高实用性。未来工作的一个方向是识别并聚合多个转向组之间的共享路段，因为这些数据实际上反映了相同的路面。通过增加一致性约束，共享路段的地图将更加直观、准确。另一个方向是区分同一转向组内的多条可能路径。例如，一个交叉口可能存在一条高架快速路，但车辆仍可在平地通行。通过调整路段高程协调过程，有可能支持这种情况。当前版本的该过程仅允许达成一个共识，尽管它能够生成代表不同水平的多个高度值。仍值得研究的是，如何确定高程序列的差异是意味着不同水平上的平行道路结构，还是高程测量精度较差所致。