PSO算法辨识时滞分段线性系统

粒子群优化算法用于具有分段线性的时滞系统

摘要

本文提出了一种用于具有分段线性的时滞系统的粒子群优化算法。通过使用切换函数，将时滞非线性系统的模型转化为辨识模型，然后基于推导出的模型，采用粒子群优化算法估计系统的所有未知参数。提供了一个示例来验证所提出算法的有效性。

关键词 ：参数估计；切换函数；分段线性；非线性系统；时间延迟。

1 引言

时滞系统常存在于工业过程中。时滞系统的辨识非常重要，因为鲁棒控制通常需要系统的参数。近年来，已存在许多辨识方法，如递推最小二乘算法、随机梯度算法和迭代算法（Yu et al., 2010；Bai, 2002；Ahmadi and Mojallali, 2011；Ding, 2013, 2014；Ding et al., 2015；Liu and Bai, 2007）。粒子群优化（PSO）算法最初旨在模拟社会行为，通常被用于估计系统参数。PSO算法常用于处理组合优化问题。

PSO算法的思想是初始化一组随机候选解，将其概念化为粒子。每个粒子被赋予一个随机速度，并在问题空间中迭代移动。粒子会朝着自身迄今为止找到的最优适应度位置以及整个种群迄今为止找到的最优适应度位置移动（徐，2013；马等，2012）。

非线性系统广泛存在于现代社会中。非线性通常分为多项式非线性和强非线性（丁等，2011；余等，2008；沃罗斯，2010；陈等，2012）。多项式非线性可以表示为变量的解析函数，而强非线性则与线性系统级联，导致强非线性的输出难以表示为变量的解析函数。因此，具有强非线性系统的辨识比具有多项式非线性系统的辨识更为困难。近年来，研究人员常采用关键项分离原理将具有强非线性的系统转化为具有多项式非线性的系统。例如，沃罗斯提出了一种适当的切换函数来建模和辨识带有间隙的哈默斯坦系统（沃罗斯，2010）。陈等提出了一种用于具有饱和和死区非线性的哈默斯坦系统的迭代算法。通过使用适当的切换函数，具有强非线性的非线性系统被简化为具有多项式非线性的系统（陈等，2012）。

本文研究具有分段线性的时滞系统的辨识问题。通过使用关键项分离技术，可将哈默斯坦系统的模型转化为辨识模型；然后基于所导出的模型，提出一种PSO算法来估计系统的未知参数。简要地，本文组织如下：第2节描述了时滞非线性系统；第3节研究了PSO算法；第4节提供了一个说明性例子；最后，第5节给出了结论性评述。

2 时滞非线性系统

考虑一个时滞非线性系统
$$
y(t) = A(z)y(t - \tau) + B(z)f(u(t)) + v(t) \tag{1}
$$
其中 $y(t)$ 是系统输出，$u(t)$ 是系统输入，$v(t)$ 是零均值的随机白噪声，$\tau$ 是时间延迟，而 $A(z)$ 和 $B(z)$ 是关于单位后移算子 $[z^{-1}y(t) = y(t - 1)]$ 的多项式，且
$$
A(z) = a_1 z^{-1} + a_2 z^{-2} + \cdots + a_n z^{-n},
$$
$$
B(z) = b_1 z^{-1} + b_2 z^{-2} + b_3 z^{-3} + \cdots + b_n z^{-n}.
$$
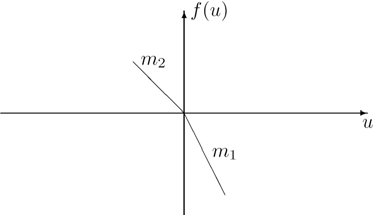
非线性输入 $f(u(t))$ 是如图1所示的分段线性函数，可表示为
$$
f(u(t)) =
\begin{cases}
m_1 u(t), & u(t) \geq 0, \
m_2 u(t), & u(t) < 0,
\end{cases}
$$
其中 $m_1$ 和 $m_2$ 是相应的分段斜率。

非线性输入 $f(u(t))$ 常被称为强非线性，因为它不能直接表示为输入的解析函数。为了简化输入，定义一个切换函数，
$$
h(u(t)) =
\begin{cases}
\frac{1}{2}, & u(t) \geq 0, \
-\frac{1}{2}, & u(t) < 0.
\end{cases}
$$
然后输出 $y(t)$ 可以表示为
$$
f(u(t)) = (m_1 - m_2)u(t)h(u(t)) + \frac{1}{2}(m_1 + m_2)u(t) \tag{2}
$$
且公式(1)可以写成
$$
y(t) = A(z)y(t - \tau) + B(z)\left[(m_1 - m_2)u(t)h(u(t)) + \frac{1}{2}(m_1 + m_2)u(t)\right] + v(t) \tag{3}
$$
由(3)可知，非线性模块的输出 $y(t)$ 可表示为输入的解析函数。

3 PSO算法

定义参数向量 $\theta$ 和信息向量 $\varphi(t)$ 为
$$
\theta = \left[b_1(m_1 - m_2), b_2(m_1 - m_2), \ldots, b_n(m_1 - m_2), \frac{1}{2}b_1(m_1 + m_2), \frac{1}{2}b_2(m_1 + m_2), \ldots, \frac{1}{2}b_n(m_1 + m_2), a_1, a_2, \ldots, a_n\right]^T \in \mathbb{R}^{n + nr}
$$
$$
\varphi(t) = [u(t-1)h(t-1), u(t-2)h(t-2), \ldots, u(t-n)h(t-n), u(t-1), u(t-2), \ldots, u(t-n), y(t-\tau), y(t-\tau-1), \ldots, y(t-n-\tau)]^T
$$
使得
$$
y(t) = \varphi^T(t)\theta + v(t) \tag{4}
$$
如果 $\theta$ 已经被估计出来，则所有辨识方案都无法从估计的 $\theta$ 中区分出 $b_j$（$j=2,3,\ldots,n$）以及 $m_l$（$l=1,2$）。因此，为了获得唯一的参数化形式，本文采用假设：第一个系数 $b_1$ 等于1，即 $b_1 = 1$。

参数向量 $\theta$ 和信息向量 $\varphi(t)$ 定义为
$$
\theta = \left[(m_1 - m_2), b_2(m_1 - m_2), \ldots, b_n(m_1 - m_2), \frac{1}{2}(m_1 + m_2), b_2(m_1 + m_2), \ldots, b_n(m_1 + m_2), a_1, a_2, \ldots, a_n\right]^T \tag{5}
$$
$$
\varphi(t) = [u(t-1)h(t-1), u(t-2)h(t-2), \ldots, u(t-n)h(t-n), u(t-1), u(t-2), \ldots, u(t-n), y(t-\tau), y(t-\tau-1), \ldots, y(t-n-\tau)]^T \tag{6}
$$
接下来，我们使用PSO算法来估计未知参数。将未知参数视为全局最优解，然后初始化一群随机解（称为粒子）$\hat{\theta}_i$，$i = 1,2,\ldots,N$，并为每个粒子分配一个随机速度 $V_i$，粒子根据自身和同伴的飞行经验进行演化。

令 $p$ 表示数据长度，并定义堆叠输出向量 $Y(p)$ 和堆叠信息矩阵 $\Phi(p)$ 为
$$
\Phi(p) = [\varphi(p), \varphi(p-1), \ldots, \varphi(1)] \in \mathbb{R}^{n + nr \times p} \tag{7}
$$
$$
Y(p) = [y(p), y(p-1), \ldots, y(1)]^T \in \mathbb{R}^p \tag{8}
$$
每个粒子具有以下位置
$$
\hat{\theta}_i = \left[(m_1 - m_2)^i, b_2(m_1 - m_2)^i, \ldots, b_n(m_1 - m_2)^i, \frac{1}{2}(m_1 + m_2)^i, b_2(m_1 + m_2)^i, \ldots, b_n(m_1 + m_2)^i, a_1^i, a_2^i, \ldots, a_n^i\right]^T
$$

粒子群优化算法用于具有分段线性的时滞系统

3 PSO算法（续）

设 $k = 1,2,3,\ldots$ 为迭代变量，$\hat{\theta}(k)$ 表示在第 $k$ 次迭代时对 $\theta$ 的估计值。在第 $k$ 次迭代中，每个粒子都有其自身的最优位置
$$
\hat{\theta} {ib}(k) = \left[(m_1 - m_2)^i(k), b_2(m_1 - m_2)^i(k), \ldots, b_n(m_1 - m_2)^i(k), \frac{1}{2}(m_1 + m_2)^i(k), b_2(m_1 + m_2)^i(k), \ldots, b_n(m_1 + m_2)^i(k), a_1^i(k), a_2^i(k), \ldots, a_n^i(k)\right]^T \tag{10}
$$
其中 $\hat{\theta} {ib}(k)$ 满足
$$
\hat{\theta} {ib}(k) = \arg\min {\theta} |Y(p) - \Phi(p)\theta(k)|^2, \quad |Y(p) - \Phi(p)\theta(k)|^2 \text{ 最小化} \tag{11}
$$
所有粒子都具有相同的全局最优位置
$$
\hat{\theta} g(k) = \left[(m_1 - m_2)^i(k), b_2(m_1 - m_2)^i(k), \ldots, b_n(m_1 - m_2)^i(k), \frac{1}{2}(m_1 + m_2)^i(k), b_2(m_1 + m_2)^i(k), \ldots, b_n(m_1 + m_2)^i(k), a_1^i(k), a_2^i(k), \ldots, a_n^i(k)\right]^T \tag{12}
$$
其中 $\hat{\theta}_g(k)$ 满足
$$
\hat{\theta}_g(k) = \arg\min {\theta} |Y(p) - \Phi(p)\theta(k)|^2, \quad i = 1,2,\ldots,N \tag{13}
$$
每个粒子都有一个新速度
$$
V_i(k+1) = V_i(k) + w[\hat{\theta} {ib}(k) - \hat{\theta}_i(k)] + c_1 r_1[\hat{\theta} {ib}(k) - \hat{\theta} i(k)] + c_2 r_2[\hat{\theta}_g(k) - \hat{\theta}_i(k)] \tag{14}
$$
其中 $c_1$ 和 $c_2$ 是介于 0 和 2 之间的正数常量（即加速系数）；$w$ 通常也是介于 0.1 和 0.9 之间的常量，用于控制之前速度对当前速度的影响，从而影响全局与局部经验之间的权衡；$r_1$ 和 $r_2$ 是两个在 $[0, 1]$ 范围内均匀分布的独立随机数。在第 $k+1$ 次迭代时，每个粒子移动到一个新位置
$$
\hat{\theta}_i(k+1) = \hat{\theta}_i(k) + V_i(k+1) \tag{15}
$$
很容易得到用于估计 $\theta$ 的 PSO 算法：
$$
\hat{\theta}_i(k+1) = \hat{\theta}_i(k) + V_i(k+1), \quad i = 1,2,\ldots,N \tag{16}
$$
$$
V_i(k+1) = V_i(k) + w[\hat{\theta} {ib}(k) - \hat{\theta} i(k)] + c_1 r_1[\hat{\theta} {ib}(k) - \hat{\theta} i(k)] + c_2 r_2[\hat{\theta}_g(k) - \hat{\theta}_i(k)] \tag{17}
$$
$$
\hat{\theta} {ib}(k) = \left[(m_1 - m_2)^i(k), b_2(m_1 - m_2)^i(k), \ldots, b_n(m_1 - m_2)^i(k), \frac{1}{2}(m_1 + m_2)^i(k), b_2(m_1 + m_2)^i(k), \ldots, b_n(m_1 + m_2)^i(k), a_1^i(k), a_2^i(k), \ldots, a_n^i(k)\right]^T \tag{18}
$$
$$
\hat{\theta} {ib}(k) = \arg\min {\theta} |Y(p) - \Phi(p)\theta(k)|^2, \quad |Y(p) - \Phi(p)\theta(k)|^2 \text{ 最小化} \tag{19}
$$
$$
\hat{\theta} g(k) = \left[(m_1 - m_2)^i(k), b_2(m_1 - m_2)^i(k), \ldots, b_n(m_1 - m_2)^i(k), \frac{1}{2}(m_1 + m_2)^i(k), b_2(m_1 + m_2)^i(k), \ldots, b_n(m_1 + m_2)^i(k), a_1^i(k), a_2^i(k), \ldots, a_n^i(k)\right]^T \tag{20}
$$
$$
\hat{\theta}_g(k) = \arg\min {\theta} |Y(p) - \Phi(p)\theta(k)|^2, \quad i = 1,2,\ldots,N \tag{21}
$$

通过 PSO 算法计算参数估计 $\hat{\theta}$ 的步骤如下所列：
1. 初始化 $N(N \geq 2)$ 个粒子，赋予其随机的位置和速度，其中每个粒子包含 $n + nr$ 个变量。给定一个很小的正数 $\varepsilon$，设置初始因子 $w = 0.72980$ 以及其他参数的值。
2. 收集输入输出数据 ${u(t), y(t)}$，$t = 1, 2, \ldots, p$，并构造 $\Phi(p)$ 和 $Y(p)$。
3. 令 $k = 1$，每个粒子自身的最优位置为 $\hat{\theta} i(1)$，速度为 $V_i(1)$，$i = 1,2,\ldots,N$。
4. 根据 (20) 计算 $\hat{\theta}_g(1)$。
5. 根据 (17) 更新每个粒子的速度 $V_i(k+1)$。
6. 根据方程 (16) 更新每个粒子的位置 $\hat{\theta}_i(k+1)$。
7. 对于每个粒子，根据 (19) 计算其自身的最优位置 $\hat{\theta} {ib}(k+1)$。
8. 根据 (20) 确定当前种群中最优粒子 $\hat{\theta}_g(k+1)$。
9. 比较 $\hat{\theta}_g(k+1)$ 和 $\hat{\theta}_g(k)$：如果 $|\hat{\theta}_g(k+1) - \hat{\theta}_g(k)| < \varepsilon$，则终止程序，得到迭代次数 $k$ 并估计 $\hat{\theta}_g(k+1)$；否则增加 $k$ 加 1 并返回到步骤 5。

4 示例

考虑以下线性动态模块，
$$
y(t) = q^{-1}y(t) - 0.1q^{-2}y(t) + [1.2 + q^{-1}]f(u(t)) + v(t)
$$
输入 ${u(t)}$ 取为具有零均值和单位方差的持续激励信号序列，${v(t)}$ 取为具有零均值和方差 $\sigma^2 = 0$ 的白噪声序列。分段线性如图1所示，其参数为：$m_1 = 1$，$m_2 = 0.8$。
然后我们得到
$$
\theta = \left[m_1 - m_2, b_2(m_1 - m_2), \frac{1}{2}(m_1 + m_2), b_2(m_1 + m_2), a\right]^T = [\alpha_1, \alpha_2, \alpha_3, \alpha_4, \alpha_5]^T = [0.2, 0.24, 0.9, 1.08, 0.1]^T
$$
$$
\varphi(t) = [h(u(t-1))u(t-1), h(u(t-2))u(t-2), u(t-1), u(t-2), y(t-1)]^T
$$
将所提出的 PSO 算法应用于估计该系统的参数，参数估计值及其误差如表1所示。

k	$\alpha_1$	$\alpha_2$	$\alpha_3$	$\alpha_4$	$\alpha_5$	$\delta(\%)$
10	0.1322	0.0899	0.8745	0.9211	0.1334	15.0681
20	0.1627	0.1436	0.8821	0.9321	0.1295	10.5034
30	0.1824	0.1763	0.8892	0.9578	0.1126	4.9921
40	0.1890	0.1882	0.8905	0.9725	0.1112	3.3514
50	0.1947	0.1926	0.9008	0.9777	0.1009	2.2431
80	0.1964	0.1952	0.8963	1.0326	0.1003	1.0002
100	0.1989	0.2002	0.8992	1.0334	0.1022	0.7482
真实值	0.2000	0.2400	0.9000	1.0800	0.1000	—

令 $\hat{\alpha}_i$ 为向量 $\hat{\theta}$ 的第 $i$ 个元素。根据 $\theta$ 的定义，我们有：
$$
\hat{m}_1 = \hat{\alpha}_1 + \hat{\alpha}_3, \quad \hat{m}_2 = \hat{\alpha}_3 - \hat{\alpha}_1
$$
由表1可知，参数估计误差随着 $k$ 的增加而变得越来越小，并趋于零。

5 结论

本文提出了一种 PSO 算法，用于辨识具有时间延迟的非线性系统。利用关键项分离技术，将非线性系统的模型转化为辨识模型；然后基于该辨识模型，提出了一种 PSO 算法来估计系统的所有参数。仿真结果验证了所提算法的有效性。