文章目录
前言
监督学习先放一下,先来学习RNN,本节课先从一个订票系统实例出发,得到前馈神经网络在相同输入只能相同输出的缺点,引入了RNN来解决这个问题。
接下来讲解了RNN常见的几种结构,尤其重点讲解了LSTM,并给出了LSTM计算实例。
公式输入请参考:在线Latex公式
实例应用引入
Slot Filling
实例论文
slot不知道怎么翻译,卡槽,槽位?
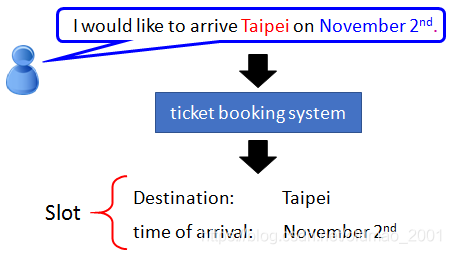
比如在一个订票系统上,我们的输入 “I would like to arrive Taipei on November
2
n
d
2^{nd}
2nd” 这样一句话(序列),我们设置几个槽位(Slot),希望算法能够将关键词’Taipei’放入目的地(Destination)槽位,将November和2nd放入到达时间(Time of Arrival)槽位,将其他词语放入其他(Other)槽位,实现对输入序列的一个归类,以便后续提取相应信息。能否用前馈神经网络(Feedforward Neural Network)来解决这个问题?
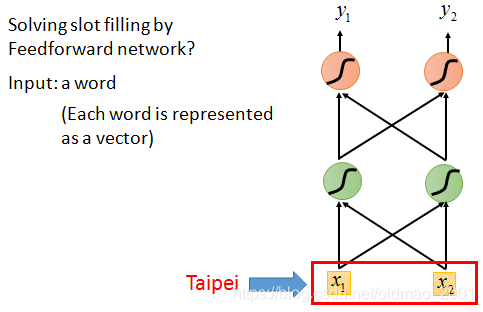
向量化
我们首先要对输入序列向量化,将每一个输入的单词用向量表示,可以使用 One-of-N Encoding 或者是 Word hashing 等编码方法,输出预测槽位的概率分布。

这个在读DEEP LEARNING REVIEW笔记一文中有写。
还有一种改进方法:Beyond 1-of-N encoding
1-of-N encoding中有很多词可能都没有见过,没有在词典里面,这个时候就可以放到Other这个dimension里面。
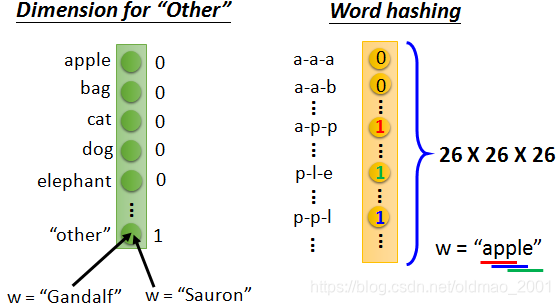
例如:“Gandalf” 甘道夫,“Sauron”索伦不在词典中,被分到other中。
也可以用词汇的数组来表示,这样就不会出现word不在词典中里面。例如“apple”里面有“app”、“ppl”、“ple”,这三个dimension是1,其他的是0。
前馈训练结果缺点
把词汇表示为vector之后,就可以把句子丢到上面那个前馈神经网络里面去。
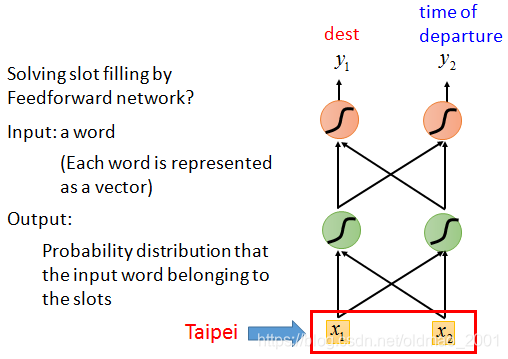
但是这样做的话,有个问题就出现了。如果现在又有一个输入是 “Leave Taipei on November
2
n
d
2^{nd}
2nd”,这里Taipei是作为一个出发地(Place of Departure),所以我们应当是把Taipei放入Departure槽位而不是Destination 槽位,但对于前馈网络来说,对于同一个输入,输出的概率分布应该也是一样的,不可能出现既是Destination的概率最高又是Departure的概率最高。
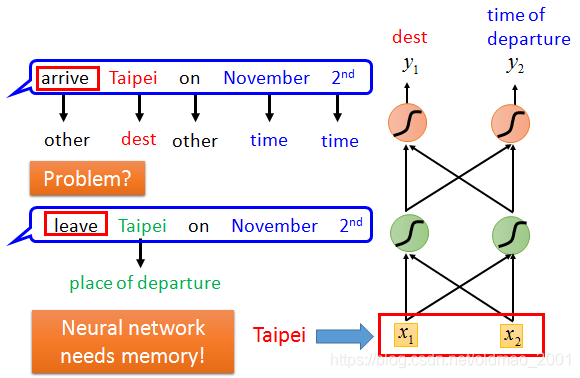
所以我们就希望能够让神经网络拥有“记忆”的能力,能够根据之前的上下文信息(在这个例子中是Arrive或Leave),相同的输入,得到不同的输出。将两段序列中的Taipei分别归入Destionation槽位和Departure槽位。这种有记忆的神经网络就是RNN。
RNN结构及小实例
RNN结构
先来看RNN的结构以及解决上面订票的问题的过程。
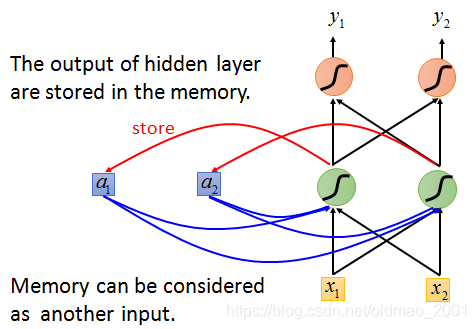
其中蓝色方框就是用于存储的隐藏层的输出的单元。下一次计算的时候,除了考虑
x
1
x_1
x1和
x
2
x_2
x2之外,还需要考虑
a
1
a_1
a1和
a
2
a_2
a2。
RNN小实例
假设有如下的神经网络结构,而且所有的权重都为1,没有bias,所有的激活函数都为线性的。
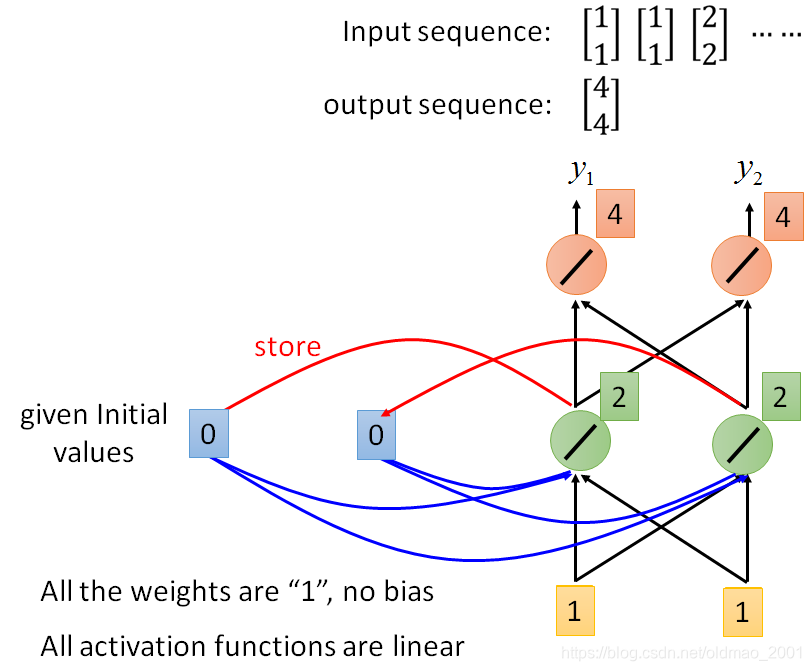
假设输入是一个sequence:
[
1
1
]
[
1
1
]
[
2
2
]
.
.
.
.
.
.
\begin{bmatrix} 1\\ 1 \end{bmatrix}\begin{bmatrix} 1\\ 1 \end{bmatrix}\begin{bmatrix} 2\\ 2 \end{bmatrix}......
[11][11][22]......
1、在计算之前,先初始化,假设
a
1
a_1
a1、
a
2
a_2
a2都为0,
x
1
x_1
x1和
x
2
x_2
x2都为1。
2、接下来绿色神经元的output为2和2,同时将输出存到
a
1
a_1
a1、
a
2
a_2
a2,即
a
1
a_1
a1、
a
2
a_2
a2都等于2,然后,红色神经元的output为4和4。即整个神经网络的输出是:
[
4
4
]
\begin{bmatrix} 4\\ 4 \end{bmatrix}
[44]
3、第二次计算如下图所示:
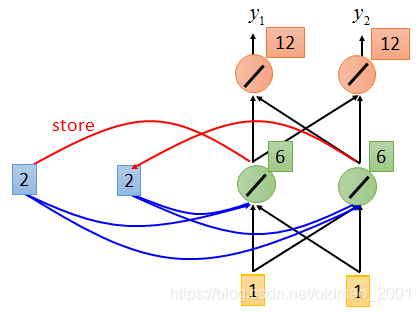
这个时候绿色神经元不但接收
x
1
x_1
x1和
x
2
x_2
x2、还接收
a
1
a_1
a1和
a
2
a_2
a2的值,所以从图中可以看出来每个绿色神经元的输出等于
x
1
+
x
2
+
a
1
+
a
2
=
2
+
2
+
1
+
1
=
6
x_1+x_2+a_1+a_2=2+2+1+1=6
x1+x2+a1+a2=2+2+1+1=6,同时会把绿色的输出存到
a
1
a_1
a1和
a
2
a_2
a2中
整个神经网络的输出:
[
4
4
]
[
12
12
]
\begin{bmatrix} 4\\ 4 \end{bmatrix}\begin{bmatrix} 12\\ 12 \end{bmatrix}
[44][1212]
这个时候可以看到即使相同的输入
[
1
1
]
\begin{bmatrix} 1\\ 1 \end{bmatrix}
[11],他的输出也是不一样的。
4、接下来的输入是
[
2
2
]
\begin{bmatrix} 2\\ 2 \end{bmatrix}
[22]结果如图:
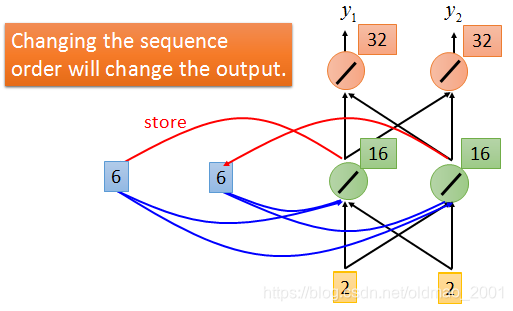
可以看出来如果改变输入sequence的顺序,输出是会变化的。
RNN解决Slot Filling问题
根据刚才的小例子,注意的是,下面不是三个神经网络,而是同一个神经网络,老师非常贴心的相同的weight都是对应相同颜色。
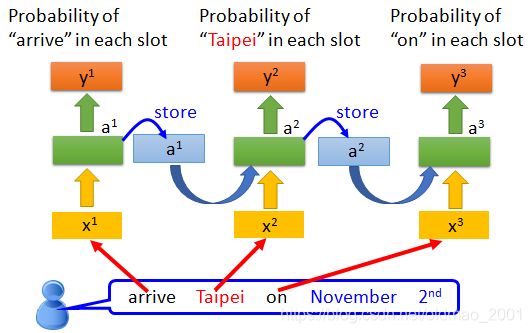
考虑不同的输入,由于第一个词不一样,所以可以看到
a
1
a^1
a1不同,因此结果不同,结果如下:
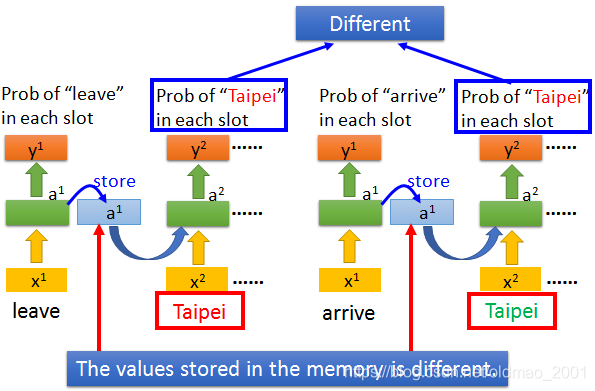
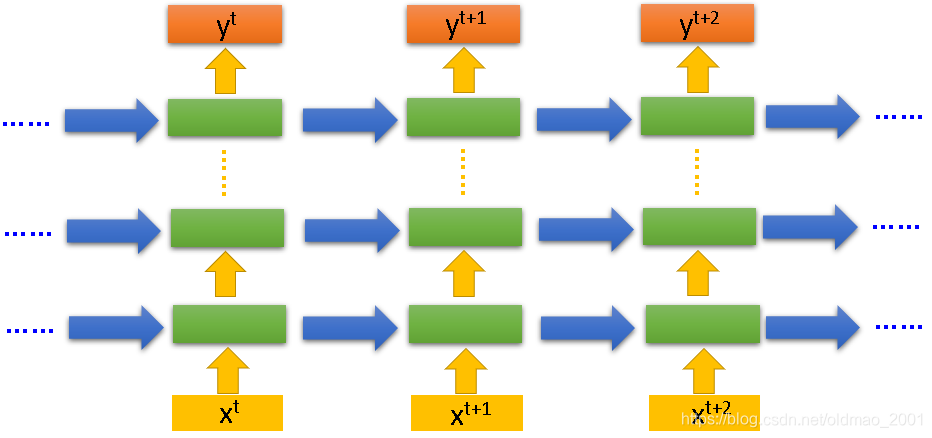
RNN的深度问题
上面的例子中的RNN只有一层隐藏层,如果要加深度是增加绿色部分就可以:
RNN的常见变种
Elman Network
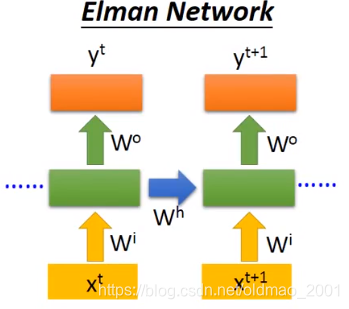
Jordan Network
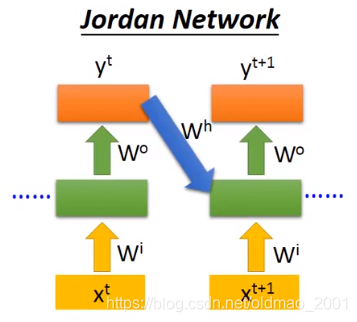
可以看到Jordan network存的不算隐藏层的输出,而是整个网络的输出,论文控给出了大概结论:Jordan network的效果好,因为在Elman network中隐藏层是很难控制的,没有办法决定它学到什么样的information;在Jordan network中y是有target的,比较清楚中间存放的是什么东西
Bidirectional RNN
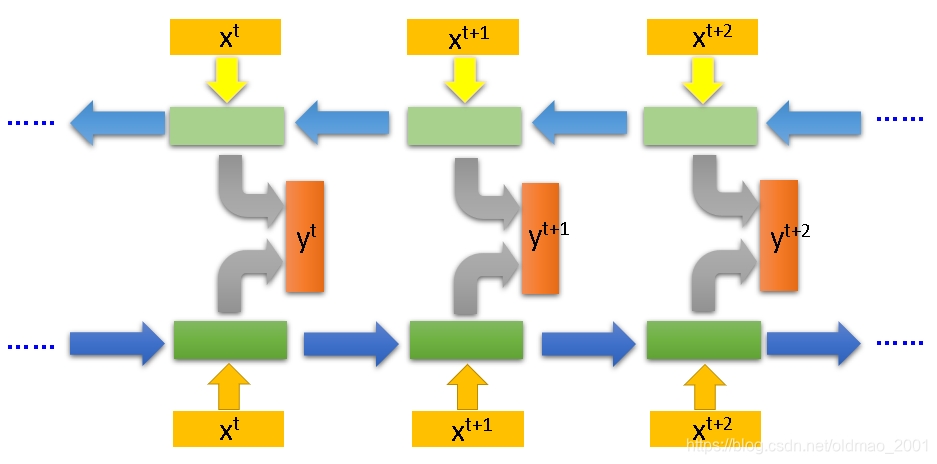
之前只有一个方向的RNN在产生
y
t
+
1
y^{t+1}
yt+1的时候,只看过
x
1
x^1
x1到
x
t
x^t
xt的输入;而Bidirectional RNN不但看过
x
1
x^1
x1到
x
t
x^t
xt的输入,还看了句尾一直到
x
t
+
1
x^{t+1}
xt+1的输入。
To determine
y
i
y_i
yi, you have to consider a lot ……
You should see the whole sequence
LSTM( Long Short-term Memory)长短时记忆
Normal neuron: 1 input, 1 output
LSTM neuron: 4 input, 1 output
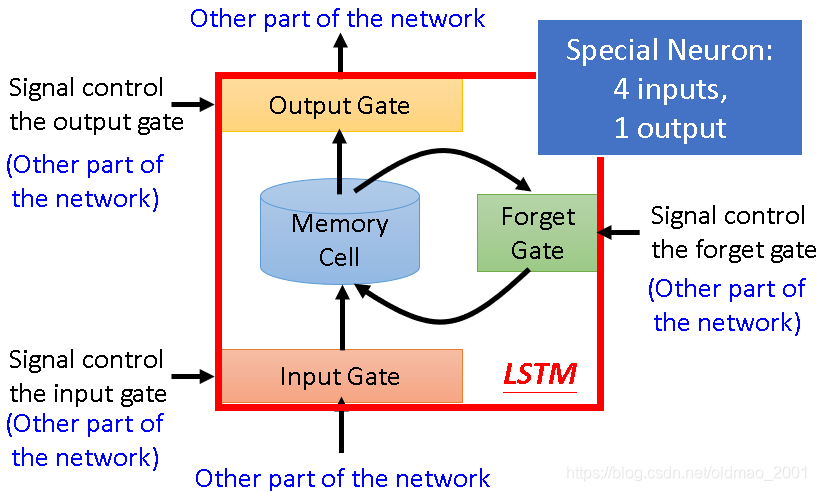
当外界信息想要写入Memory Cell必须先经过Input gate,input gate打开的时候才能把值写入Memory Cell,Input gate打开还是关闭状态是LSTM自己学的。同样原理还有Forget Gate,Ourput Gate。
PS:冷知识,Long Short-term的-要放在short和term之间,因为从原理上看,整个Memory还是短期的,只不过整个这个短期Memory比较长(只要你的Forget gate不format Memory cell里面的值都会一直保留)。
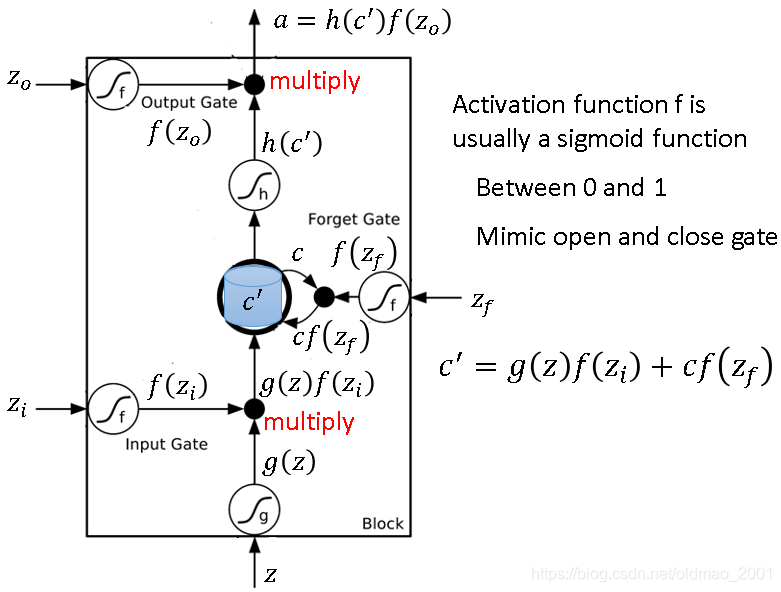
在上图中,
z
i
z_i
zi、
z
0
z_0
z0都是向量scalar,三个门使用的激活函数通常是sigmoid函数,因此输出的范围为0到1,代表门打开的程度,1是打开,0是关闭。上图中的Memory Cell中本来是
c
c
c,后来经过右边公式操作后变成
c
′
c'
c′。注意:Forget Gate打开的时候表示记得,关闭代表忘记。
LSTM实例
输入是三维vector
[
x
1
x
2
x
3
]
\begin{bmatrix} x_1\\ x_2\\ x_3 \end{bmatrix}
⎣⎡x1x2x3⎦⎤,输出是一维vector
y
y
y,神经网络中只有一个LSTM的CELL。
当输入中的
x
2
=
1
x_2=1
x2=1,
x
1
x_1
x1的值就会被累加写到Memory中;
当输入中的
x
2
=
−
1
x_2=-1
x2=−1,Memory中的值就会Reset;
当输入中的
x
3
=
1
x_3=1
x3=1,output gate才会打开,才输出Memory中的内容
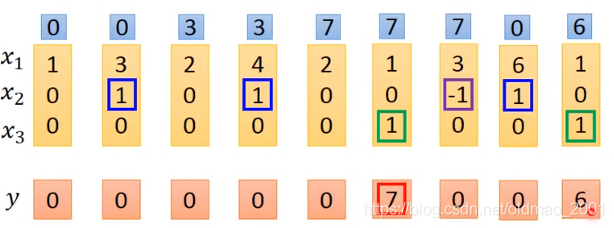
注意:第一次出现
x
2
=
1
x_2=1
x2=1(蓝色框),就把当前
x
1
=
3
x_1=3
x1=3写入下一个时间点的memory中;
第二次出现
x
2
=
1
x_2=1
x2=1,,就把当前
x
1
=
4
x_1=4
x1=4和
m
e
m
o
r
y
=
3
memory=3
memory=3累加,变成
m
e
m
o
r
y
=
7
memory=7
memory=7;
第一次出现
x
2
=
−
1
x_2=-1
x2=−1(紫色框),就把下一个时间点的memory清空;
当出现
x
3
=
1
x_3=1
x3=1(绿色框),就把memory里面的值输出。
按上面的规则来实际计算一下:
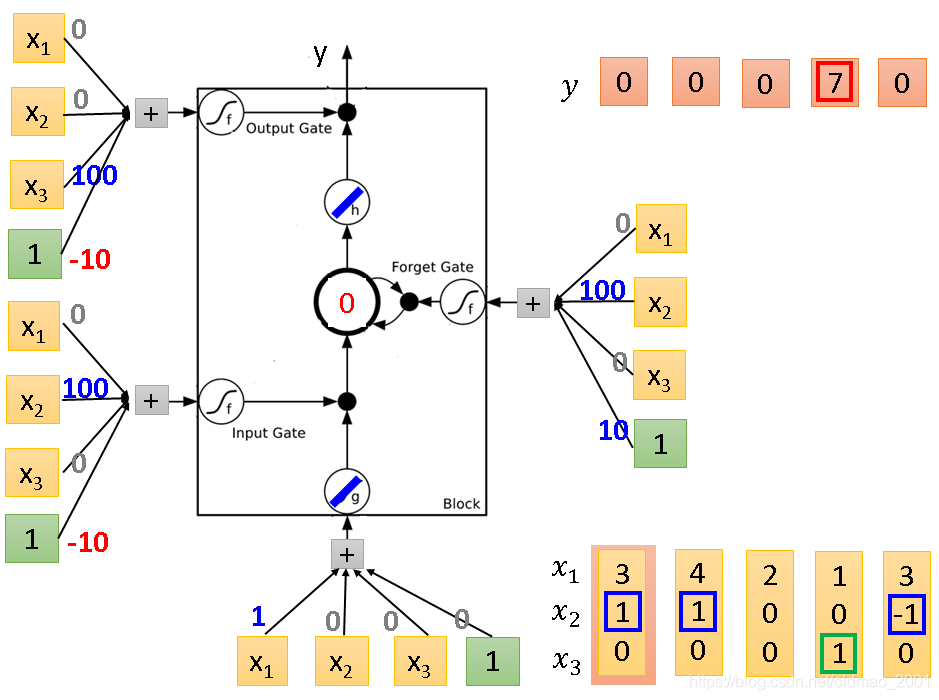
输入要乘以权重加上bias才是输出,权重本来是应该用GD学习得来,现在暂且当做已知条件(蓝色数字)。
存在Memory(中间那个圈圈)的初始值为0
下面开始输入第一组
[
x
1
x
2
x
3
]
\begin{bmatrix} x_1\\ x_2\\ x_3 \end{bmatrix}
⎣⎡x1x2x3⎦⎤,即右下角第一组
[
3
1
0
]
\begin{bmatrix} 3\\ 1\\ 0 \end{bmatrix}
⎣⎡310⎦⎤
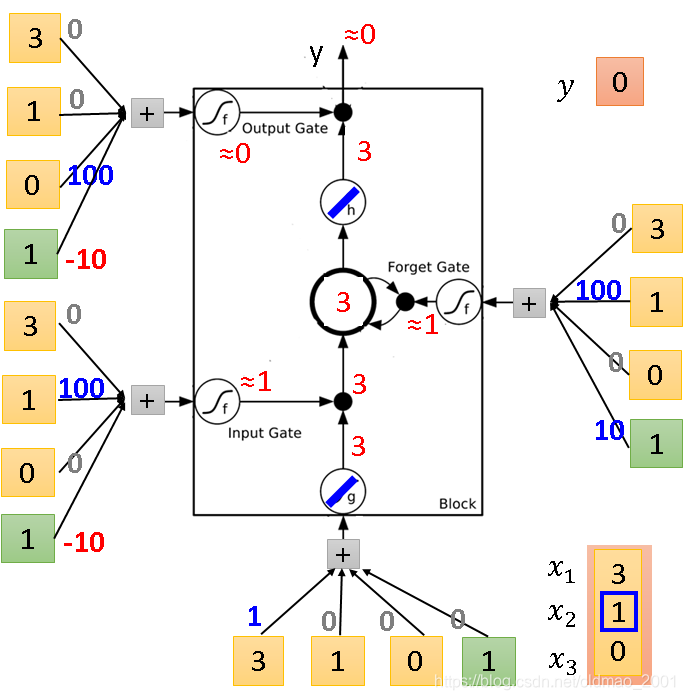
输入部分:
3
×
1
+
1
×
0
+
0
×
0
+
1
×
0
=
3
3×1+1×0+0×0+1×0=3
3×1+1×0+0×0+1×0=3通过线性激活函数g得到3
Input Gate:
3
×
0
+
1
×
100
+
0
×
0
+
1
×
(
−
10
)
=
90
3×0+1×100+0×0+1×(-10)=90
3×0+1×100+0×0+1×(−10)=90通过sigmoid函数约等于1,Input Gate打开,输入的3往下走
Forget Gate:
3
×
0
+
1
×
100
+
0
×
0
+
1
×
10
=
110
3×0+1×100+0×0+1×10=110
3×0+1×100+0×0+1×10=110通过sigmoid函数约等于1,Forget Gate打开,memory记录3,然后经过线性激活函数h得到3
Output Gate:
3
×
0
+
1
×
0
+
0
×
100
+
1
×
(
−
10
)
=
−
10
3×0+1×0+0×100+1×(-10)=-10
3×0+1×0+0×100+1×(−10)=−10通过sigmoid函数约等于0,Output Gate关闭,输出y为0。
同理,下面开始输入第二组r
[
x
1
x
2
x
3
]
\begin{bmatrix} x_1\\ x_2\\ x_3 \end{bmatrix}
⎣⎡x1x2x3⎦⎤,即右下角第二组
[
4
1
0
]
\begin{bmatrix} 4\\ 1\\ 0 \end{bmatrix}
⎣⎡410⎦⎤
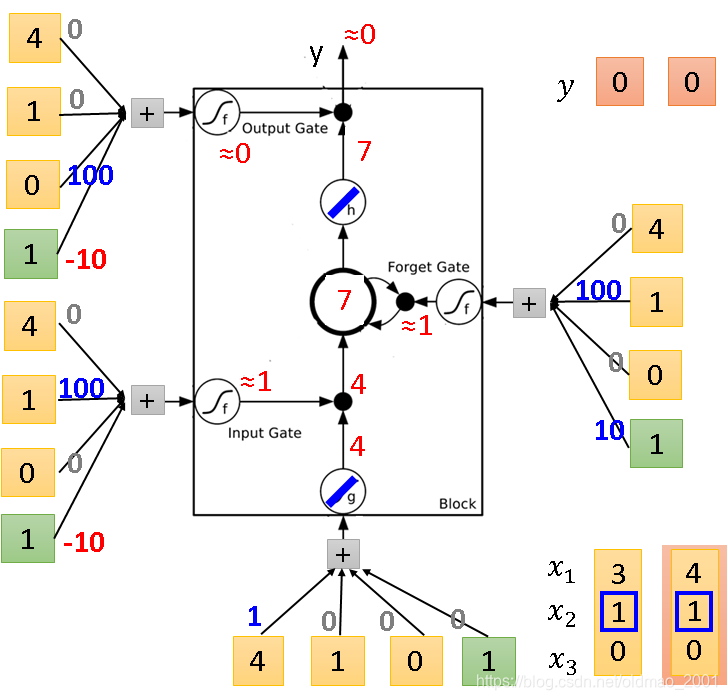
与第一次不一样的地方是Forget Gate把传过来的4累加到memory中变成了7。
第三组输入
[
2
0
0
]
\begin{bmatrix} 2\\ 0\\ 0 \end{bmatrix}
⎣⎡200⎦⎤
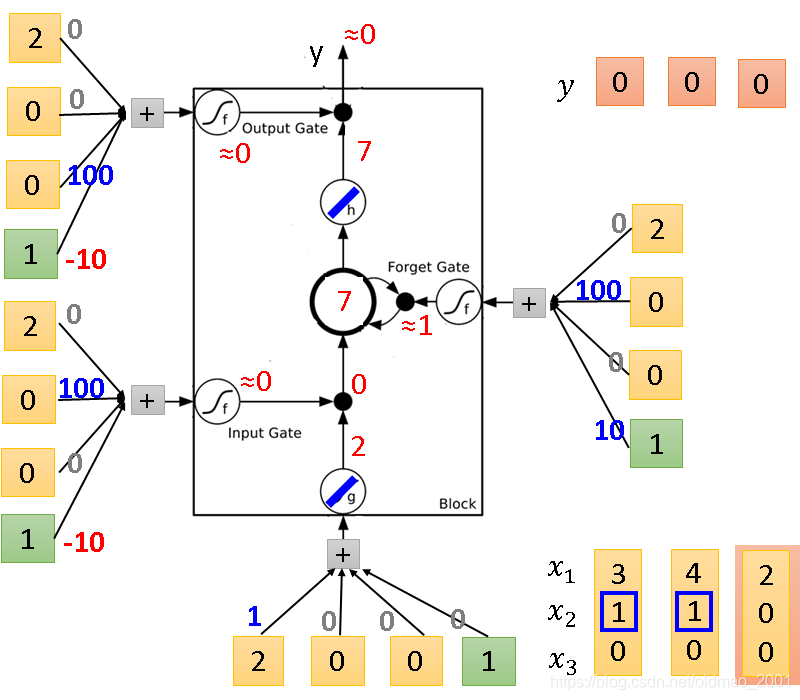
第四组输入
[
1
0
1
]
\begin{bmatrix} 1\\ 0\\ 1 \end{bmatrix}
⎣⎡101⎦⎤
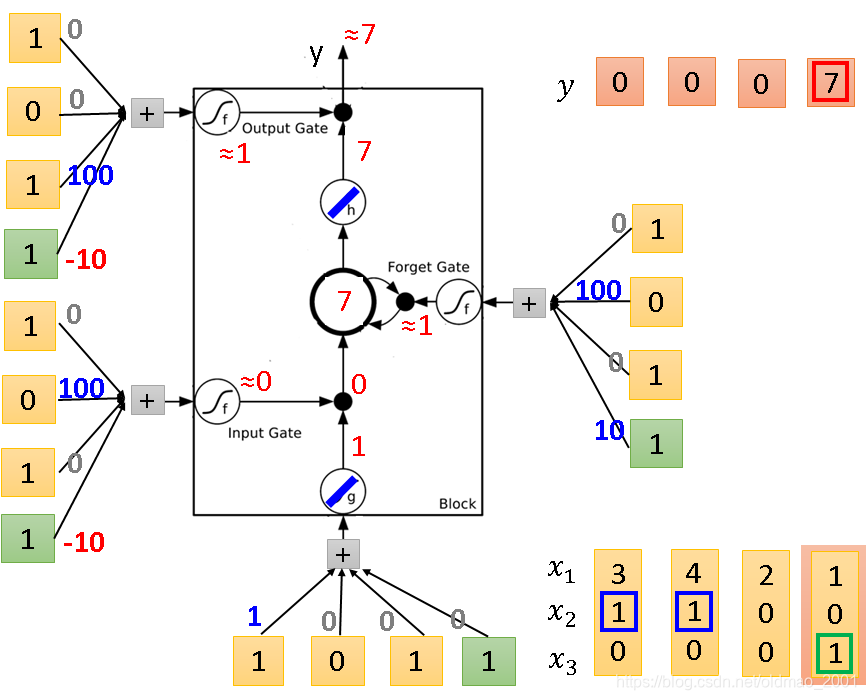
第四组输入
[
3
−
1
0
]
\begin{bmatrix} 3\\ -1\\ 0 \end{bmatrix}
⎣⎡3−10⎦⎤
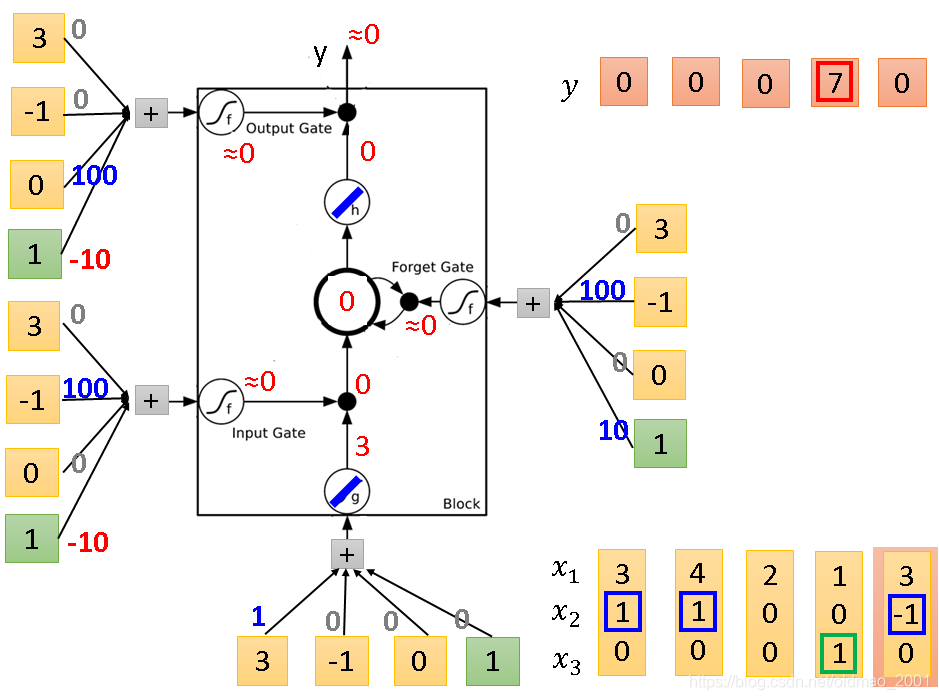
这里Forget Gate计算后的值为-90,经过sigoid后变0,Forget Gate会关闭,并清空memory中的值。
普通NN变身LSTM过程
假设现在有这样一个神经网络:
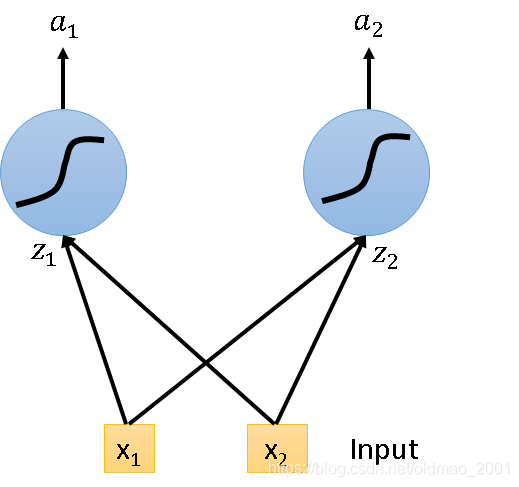
变身为LSTM只要Simply replace the neurons with LSTM,就变成:
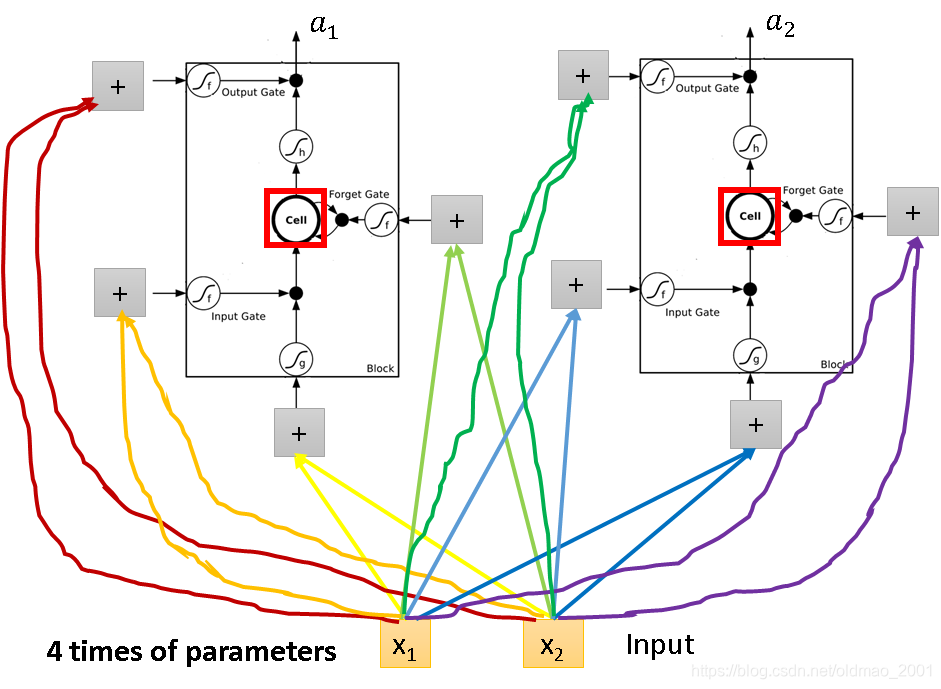
可以看出来神经元一样的情况下,LSTM的参数是普通RNN参数的4倍。
LSTM与RNN啥关系
上面的图貌似看不出来LSTM是RNN,现在整理一下:
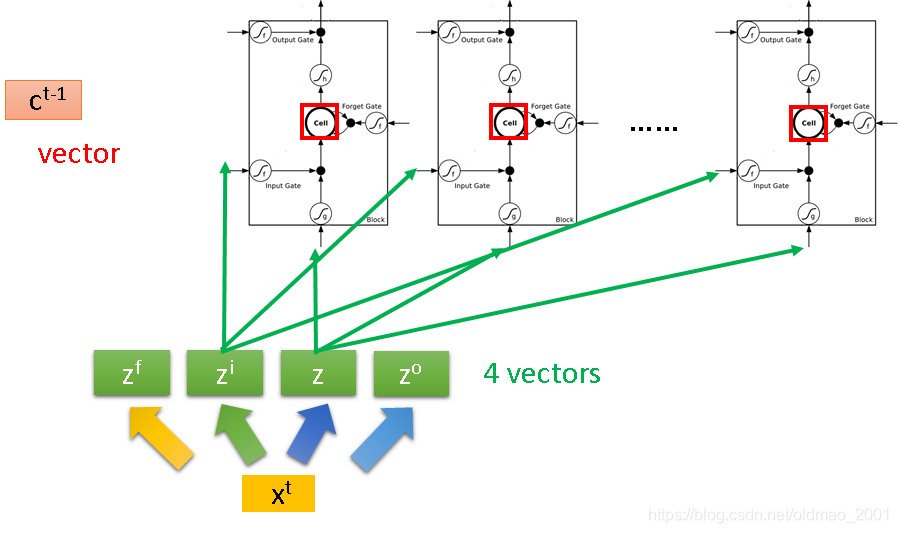
假设我们有一整排的LSTM神经元,他们每个memory cell里面都存了一个值scalar。把这些scalar连起来,可以写成
c
t
−
1
c^{t-1}
ct−1,现在在时间点
t
t
t输入一个vector:
X
t
X^t
Xt,
这个
X
t
X^t
Xt会先乘上一个matrix,做linear的transform,变成vector:
Z
Z
Z,它的dimension对应的是每一个LSTM神经元输入,所以这个dimension的大小等于LSTM神经元的数量;
这个
X
t
X^t
Xt会先乘上一个matrix,做linear的transform,变成vector:
Z
i
Z^i
Zi,它的dimension的大小等于LSTM神经元的数量,
Z
i
Z^i
Zi对应于LSTM神经元的input gate;
同理
Z
f
Z^f
Zf对应于LSTM神经元的forget gate;
同理
Z
o
Z^o
Zo对应于LSTM神经元的output gate;
整个计算过程可以表示为下图,注意右边的四个绿色的东西是向量中的一个dimension:
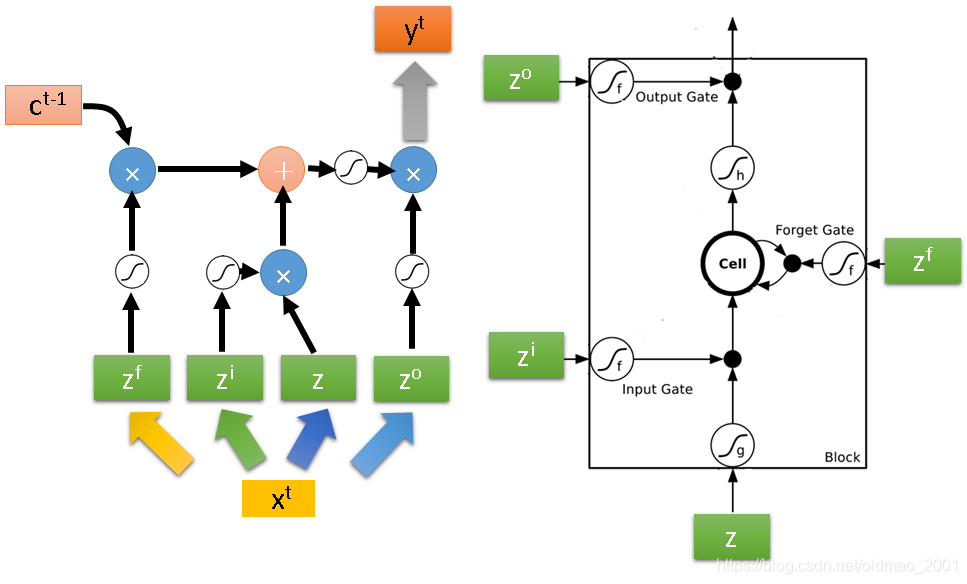
X
t
X^t
Xt到
X
t
+
1
X^{t+1}
Xt+1时间点的LSTM计算如下图:
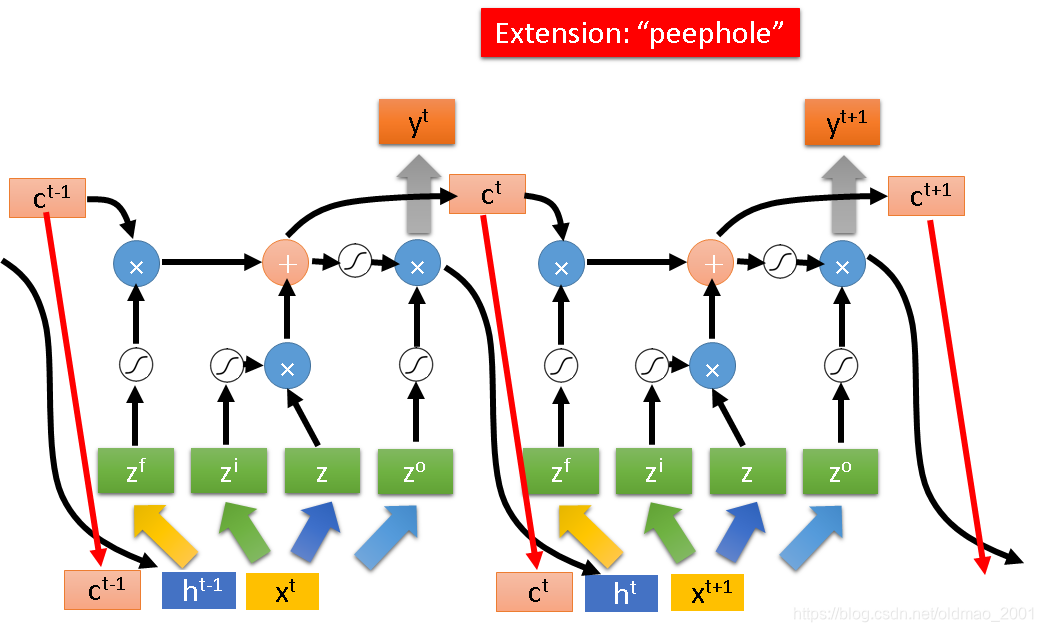
这里比上面的图要多了两个东西,输入的地方除了
X
t
X^t
Xt之外,还会接入上一个LSTM神经元隐藏层的输出
h
t
−
1
h^{t-1}
ht−1,还会把memory cell中的值
c
t
−
1
c^{t-1}
ct−1(红色箭头表示,这个叫peephole),也就是说输入的东西由三个vector并在一起,乘上不同的transform,操控不同的gate。
上面是单层LSTM,下面多层LSTM感受一下。。。
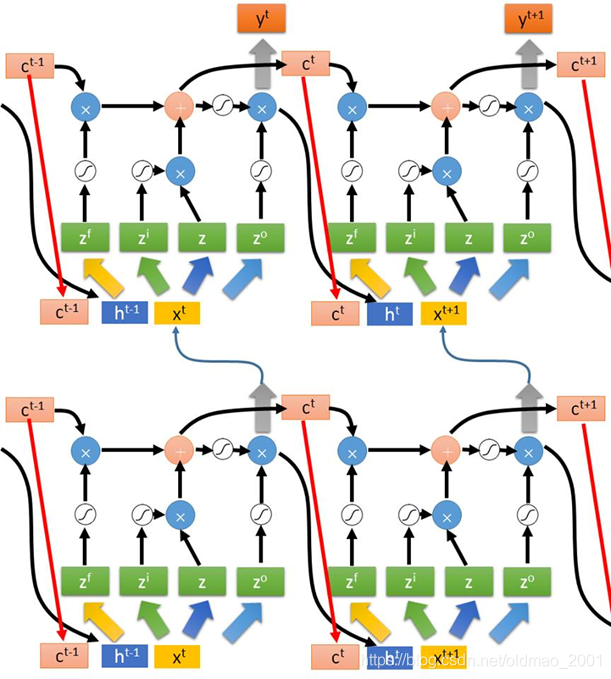
老师表示看不懂没关系,会调包就可以。






 本文探讨了循环神经网络(RNN)及其变种长短时记忆网络(LSTM)在SlotFilling任务中的应用,通过实例展示了如何利用RNN解决序列分类问题,并深入解析了LSTM的结构与工作原理。
本文探讨了循环神经网络(RNN)及其变种长短时记忆网络(LSTM)在SlotFilling任务中的应用,通过实例展示了如何利用RNN解决序列分类问题,并深入解析了LSTM的结构与工作原理。

















 5459
5459












