文章目录
前言
以后笔记里面都要加这节,相当于把总结放前面,有什么新的感悟也丢这里。
反向传播的推导老师有额外的一个视频,具体看一节课的笔记。
ng的深度学习里面号称这个推导是ML里面最为复杂的。
自我感觉其实不难,只不过里面的数学标记notation特别的多,容易搞混,最基础的链式法则明白,推导看得懂是没有问题的。
重点:李宏毅讲这个与ng不一样的地方就是在于他把反向传播的过程又看成一个神经网络,这个理解就很牛叉。
在线Latex公式
前情提要:previous on NN
接上节课的内(da)容(keng),上回书说到我们想用梯度下降的方式来训练一个神经网络应该怎么做:

其中困难的地方在于,参数太多,如果有效的计算梯度?答案就是反向传播算法。所以这个算法的本质就是神经网络版的梯度下降算法。
基础知识Chain rule
很简单的数学基础,直接看例子就知道,实际上就是复合函数求导。
示例1:
y
=
g
(
x
)
z
=
h
(
y
)
y=g(x)\quad \quad z=h(y)
y=g(x)z=h(y)
Δ
x
→
Δ
y
→
Δ
z
d
z
d
x
=
d
z
d
y
d
y
d
x
\Delta{x}\rightarrow\Delta{y}\rightarrow\Delta{z}\quad \quad \frac{dz}{dx}=\frac{dz}{dy}\frac{dy}{dx}
Δx→Δy→Δzdxdz=dydzdxdy
示例2:
x
=
g
(
s
)
y
=
h
(
s
)
z
=
k
(
x
,
y
)
x=g(s)\quad \quad y=h(s)\quad \quad z=k(x,y)
x=g(s)y=h(s)z=k(x,y)
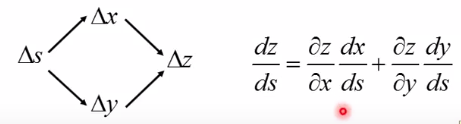
PS:上面的图咋用latex公式输入?
反向传播 backpropagation
先祭出反向传播的代价函数:
L
(
θ
)
=
∑
n
=
1
N
C
n
(
θ
)
L(θ)=\sum_{n=1}^{N}C^n(θ)
L(θ)=n=1∑NCn(θ)
其中
C
n
C^n
Cn是
y
n
y^n
yn和
y
^
n
\widehat{y}^n
y
n之间的距离,
C
n
C^n
Cn大代表loss大,
C
n
C^n
Cn小则loss较小,这个时候参数
θ
θ
θ是比较好的。如下图所示是输入一个training data
x
n
x^n
xn,输出一个
y
n
{y}^n
yn:
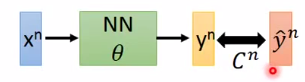
代价函数中的求和就是把所有training data的输出
y
n
{y}^n
yn和目标
y
^
n
\hat{y}^n
y^n距离加起来,然后求最小值,求极值就是求导数拉:
∂
L
(
θ
)
∂
w
=
∑
n
=
1
N
∂
C
n
(
θ
)
∂
w
\cfrac{\partial L(θ)}{\partial w}=\sum_{n=1}^{N}\cfrac{\partial{C^n(θ)}}{\partial w}
∂w∂L(θ)=n=1∑N∂w∂Cn(θ)
这个问题按上面的公式就变成计算某一笔training data的偏导,然后再求和,所以问题集中在如何计算:
∂
C
n
(
θ
)
∂
w
\cfrac{\partial{C^n(θ)}}{\partial w}
∂w∂Cn(θ)
先从下图中的神经网络中的一个神经元来看
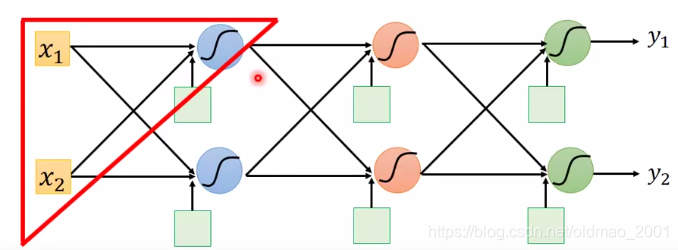
把红色三角部分拿出来,这个神经元是在第一层的第一个,他的输入是
x
1
,
x
2
x_1,x_2
x1,x2
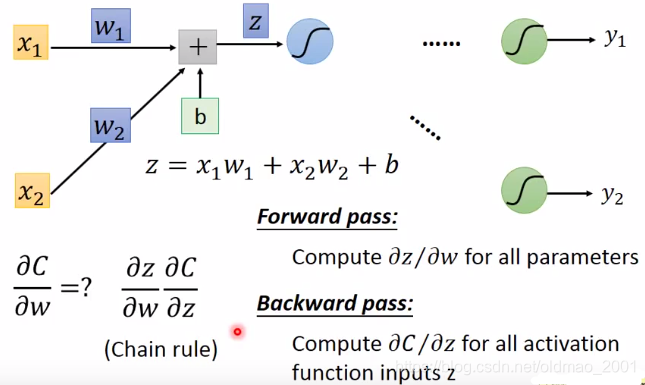
计算前向 ∂ z / ∂ w \partial z/\partial w ∂z/∂w
先看函数的样子,接上页:
z
=
x
1
w
1
+
x
2
w
2
+
b
z=x_1w_1+x_2w_2+b
z=x1w1+x2w2+b
求
∂
z
/
∂
w
1
=
?
\partial z/\partial w_1=?
∂z/∂w1=?,秒算结果为
x
1
x_1
x1
∂
z
/
∂
w
2
=
?
\partial z/\partial w_2=?
∂z/∂w2=?,秒算结果为
x
2
x_2
x2
前向传播的过程中,
∂
z
/
∂
w
\partial z/\partial w
∂z/∂w的结果规律就是连接weight
w
w
w的输入
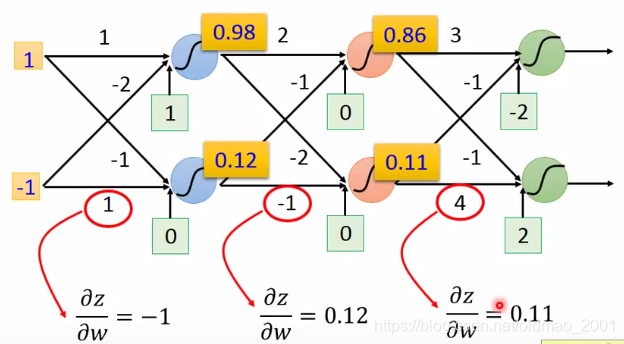
从图中可以看出forward pass的过程很直白。
计算反向 ∂ C / ∂ z \partial C/\partial z ∂C/∂z
先上图:
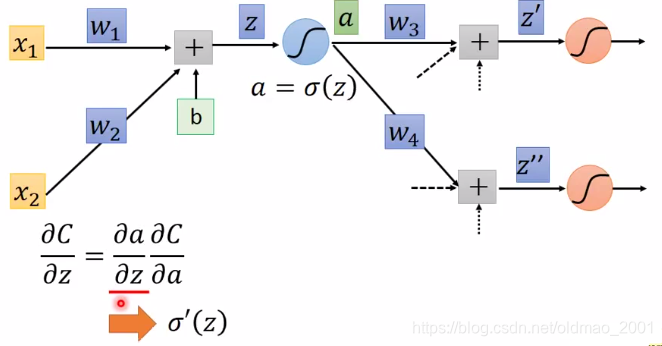
其中求
σ
′
(
z
)
σ'(z)
σ′(z)可以自己推导,比较笨(lan)的就把结果当公式背下来。
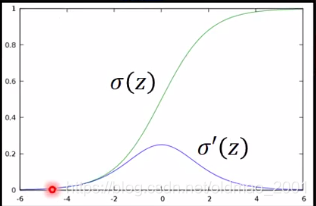
这里看不懂的看下上面的基础知识的示例2
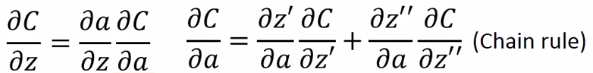
这里:
∂
z
′
∂
a
\cfrac{\partial z'}{\partial a}
∂a∂z′是前向里面讲过的,就是秒算的
w
3
w_3
w3
同理:
∂
z
′
′
∂
a
\cfrac{\partial z''}{\partial a}
∂a∂z′′是前向里面讲过的,就是秒算的
w
4
w_4
w4
PS:老师的这个计算过程中的w的下标没有ng的例子里面讲得严谨啊,不过不影响理解算法。
现在假设
∂
C
∂
z
′
\cfrac{\partial C}{\partial z'}
∂z′∂C和
∂
C
∂
z
′
′
\cfrac{\partial C}{\partial z''}
∂z′′∂C已经算出来,带入前面的式子:
∂
C
∂
z
=
σ
′
(
z
)
[
w
3
∂
C
∂
z
′
+
w
4
∂
C
∂
z
′
′
]
\frac{\partial C}{\partial z}=\sigma'(z)\left [w_3\frac{\partial C}{\partial z'}+w_4\frac{\partial C}{\partial z''}\right]
∂z∂C=σ′(z)[w3∂z′∂C+w4∂z′′∂C]
接下来是个人认为李宏毅理解反向传播最牛叉的地方咯
上面的公式可以看成一个神经网络,他的正向传播过程就是原神经网络的反向传播。
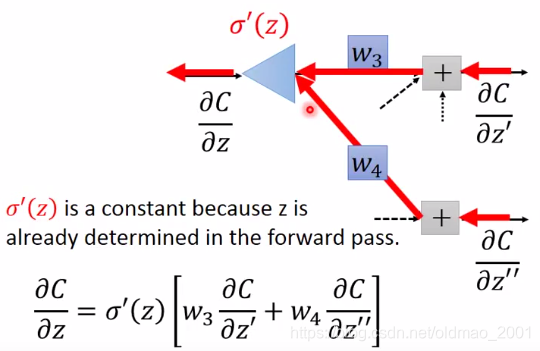
只不过激活函数是乘上一个常数
σ
′
(
z
)
\sigma'(z)
σ′(z)(之所以是常数是因为之前前向传播过程中这个东西是算出来了的。)
PS:至于为什么这里神经元的形状是三角形因为老师自称是电气系 ,里面乘以系数就和放大器一样,所以用运算放大器(Operational Amplifier,简称 OP、OPA、OPAMP)的图标三角形表示。
回到正题,刚才我们有假设
∂
C
∂
z
′
\cfrac{\partial C}{\partial z'}
∂z′∂C和
∂
C
∂
z
′
′
\cfrac{\partial C}{\partial z''}
∂z′′∂C是已知,现在就分两种情况来求一下这两项。
情况一:输出层
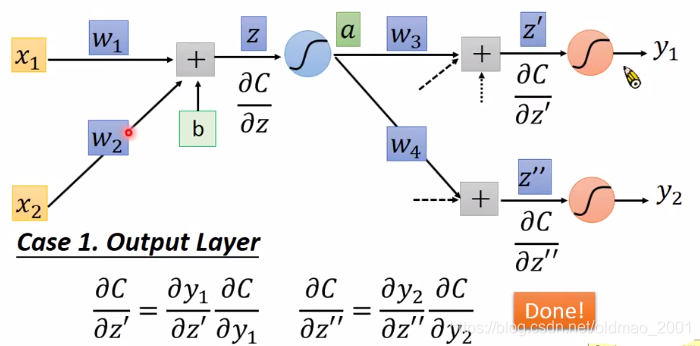
这个情况算是比较简单,其中:
∂
y
1
∂
z
′
\cfrac{\partial y_1}{\partial z'}
∂z′∂y1这个求导和最后输出层的激活函数有关;
∂
C
∂
y
1
\cfrac{\partial C}{\partial y_1}
∂y1∂C这个求导和最后求
y
n
y^n
yn和
y
^
n
\hat{y}^n
y^n之间的距离函数有关,例如你可以用均方差,可以用交叉熵等等。
情况二:非输出层
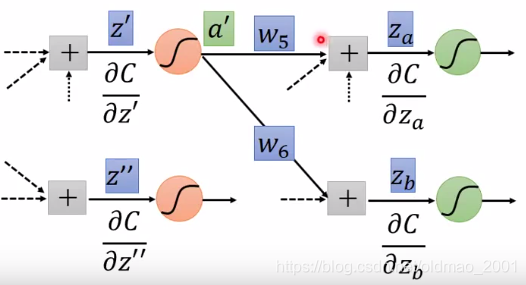
上图中如果
∂
C
∂
z
a
\cfrac{\partial C}{\partial z_a}
∂za∂C和
∂
C
∂
z
b
\cfrac{\partial C}{\partial z_b}
∂zb∂C是已知的,就可以利用上面的新神经网络计算反向的
∂
C
∂
z
′
\cfrac{\partial C}{\partial z'}
∂z′∂C
计算方式就是按箭头的方向进行前向计算:
∂
C
∂
z
′
=
(
∂
C
∂
z
a
w
5
+
∂
C
∂
z
b
w
6
)
⋅
σ
′
(
z
′
)
\cfrac{\partial C}{\partial z'}=\left(\cfrac{\partial C}{\partial z_a}w_5+\cfrac{\partial C}{\partial z_b}w_6\right)\cdot\sigma'(z')
∂z′∂C=(∂za∂Cw5+∂zb∂Cw6)⋅σ′(z′)
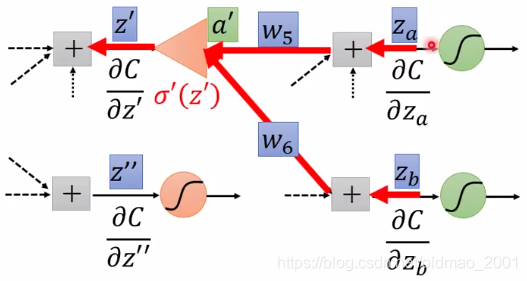
这样就进入了迭代,如果上图的绿色的神经元是输出,则按情况一,秒算。
如果不是输出层,则继续推下一层,往下算,直到输出层为止。
貌似很复杂,但是如果一开始就从输出层开始往回算,就很简单。
这个原理后来听了CS231n后发现和计算图有点像。
反向计算
实际上的计算应该是这样的:
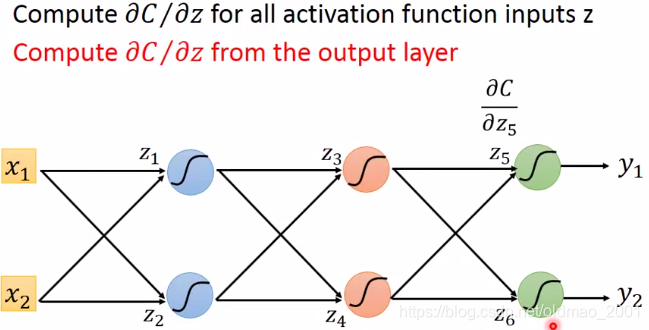
之前的一开始就从
z
1
,
z
2
z_1,z_2
z1,z2开始算对C的偏导,发现算
z
1
,
z
2
z_1,z_2
z1,z2对C的偏导要先知道
z
3
,
z
4
z_3,z_4
z3,z4对C的偏导,算
z
3
,
z
4
z_3,z_4
z3,z4对C的偏导要先知道
z
5
,
z
6
z_5,z_6
z5,z6对C的偏导,崩溃ing。。。
现在如果从后面往前反向计算呢?
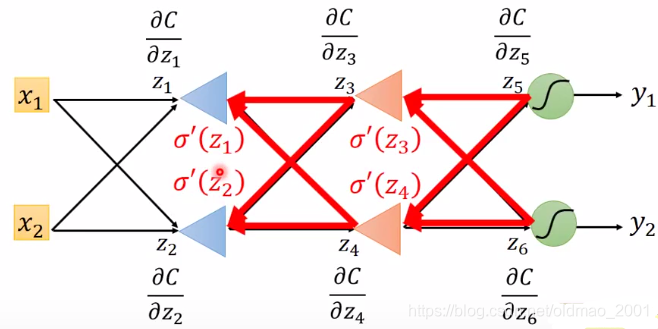
这里就是反向神经网络的最终形态,它除了原来的输出层之外,其他所有层的神经元的激活函数是通过之前的forward pass计算出来的
σ
′
(
z
)
\sigma'(z)
σ′(z),然后再在这个新的反向神经网络上做forward pass,就可以计算每一项
∂
C
∂
z
\cfrac{\partial C}{\partial z}
∂z∂C,以
∂
C
∂
z
3
\cfrac{\partial C}{\partial z_3}
∂z3∂C为例:
∂
C
∂
z
3
=
σ
′
(
z
3
)
[
w
9
∂
C
∂
z
5
+
w
10
∂
C
∂
z
6
]
\cfrac{\partial C}{\partial z_3}=\sigma'(z_3)\left [w_9\cfrac{\partial C}{\partial z_5}+w_{10}\cfrac{\partial C}{\partial z_6}\right]
∂z3∂C=σ′(z3)[w9∂z5∂C+w10∂z6∂C]
w
9
,
w
10
w_9,w_{10}
w9,w10就是指向
z
3
z_3
z3的权重。
总结
实际就是下图:
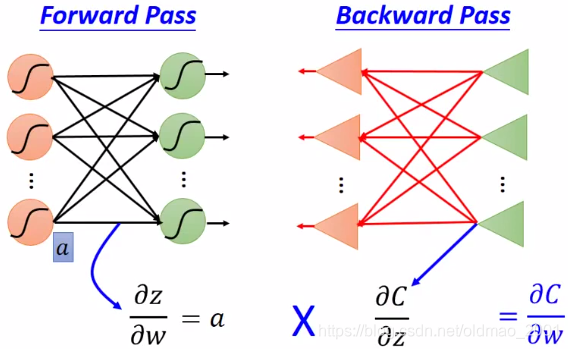
总之是比较好理解,但是没有ng的严谨。





 本文围绕反向传播算法展开,指出其本质是神经网络版的梯度下降算法。介绍了链式法则这一基础知识,详细推导了反向传播中前向∂z/∂w和反向∂C/∂z的计算,分输出层和非输出层两种情况讨论,还说明了反向计算的过程,最后总结该算法较好理解但不如ng的严谨。
本文围绕反向传播算法展开,指出其本质是神经网络版的梯度下降算法。介绍了链式法则这一基础知识,详细推导了反向传播中前向∂z/∂w和反向∂C/∂z的计算,分输出层和非输出层两种情况讨论,还说明了反向计算的过程,最后总结该算法较好理解但不如ng的严谨。

















 1408
1408

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










