番外.李宏毅学习笔记.ST3.Structured SVM

公式输入请参考： 在线Latex公式
课程PPT
Structured SVM和之前的一个SVM的课还不一样，之前的SVM是Structured SVM的一个特例。

前情回顾（略）

Separable case

也就是SVM里面提到过的，数据是线性可分的，也就是说存在一个权重向量$\hat{w}$使得：
$$\begin{gathered} \hat{w}\cdot \varphi (x^1,{\hat{y}}^1)\ge \hat{w}\cdot \varphi (x^1,y)+\delta \\ \hat{w}\cdot \varphi (x^2,{\hat{y}}^2)\ge \hat{w}\cdot \varphi (x^2,y)+\delta \end{gathered}$$

Structured Perceptron

其实是上节提到过的，还没有证明的算法。这里贴过来（和上节不一样的是x，y的上标由r变成了n）：
算法描述：
输入：训练集：
{ ( x 1 , y ^ 1 ) , ( x 2 , y ^ 2 ) , . . . , ( x N , y ^ N ) , . . . } \{(x^1,\widehat y^1),(x^2,\widehat y^2),...,(x^N,\widehat y^N),...\} {(x1,y ​1),(x2,y ​2),...,(xN,y ​N),...}
输出：权重向量$w$
伪代码（$w$存在是前提条件）
Initialize $w=0$
$do$
For each pair of training example $(x^n,{\hat{y}}^n$取一笔训练数据
Find the label ${\tilde{y}}^n$ maximizing $w\cdot \varphi (x^n,y)$
$${\tilde{y}}^n=arg\underset{y\in Y}{\max }w\cdot \varphi (x^n,y)这个是question2$$，这个之前假设这个问题已经解决了
if ${\tilde{y}}^n\ne {\hat{y}}^n$, update $w$
$$w\to w+\varphi (x^n,{\hat{y}}^n)-\varphi (x^n,{\tilde{y}}^n)$$
$untilwisnotupdated\to$ We are done!
下面开始证明：

Warning of Math

前戏

在本节的假定中，数据是线性可分的，为了找到$\hat{w}$，我们最多需要更新$(\frac{R}{\delta }{)}^2$次
其中：$\delta$是margin，R是$\varphi (x,y)$与$\varphi (x,y^{\prime })$的最大距离。
注意：算法的迭代次数和y的个数无关。
证明开始：
每次看到一个错误（${\tilde{y}}^n\ne {\hat{y}}^n$）$w$就更新一次，所以更新的思路是：
$$w^0=0\to w^1\to w^2\to \cdots \to w^k\to w^{k+1}\to \cdots$$
$$w^k=w^{k-1}+\varphi (x^n,{\hat{y}}^n)-\varphi (x^n,{\tilde{y}}^n)\text{\hspace{1em}(1)}$$
以上就是$w^k$和$w^{k-1}$的关系。
当然不要忘记我们的前提条件：
数据是线性可分的，存在一个权重向量$\hat{w}$使得：
对于所有训练数据$\forall n$，和所有数据对应的所有不正确的标签 ∀ y ∈ Y − { y ^ n } \forall y\in Y-\{\widehat y^n\} ∀y∈Y−{y ​n}：
$$\hat{w}\cdot \varphi (x^n,{\hat{y}}^n)\ge \hat{w}\cdot \varphi (x^n,y)+\delta$$
对于$\hat{w}$，我们不是一般性的假设其长度为1：$||\hat{w}||=1$（因为向量总是可以做normalization，使得长度变成1，所以为了便于计算，就直接定为1好了。）

开证

记${\rho }_k$为$\hat{w}$和$w^k$的夹角，要证明：随着k的增加，这个夹角是越来越小的。即$cos{\rho }_k$是越来越大的。
$$cos{\rho }_k=\frac{\hat{w}}{||\hat{w}||}\cdot \frac{w^k}{||w^k||}$$
先看分子，是$\hat{w}$和$w^k$的点积，把前戏中的公式2带入：
$$\begin{gathered} \hat{w}\cdot w^k=\hat{w}\cdot (w^{k-1}+\varphi (x^n,{\hat{y}}^n)-\varphi (x^n,{\tilde{y}}^n)) \\ =\hat{w}\cdot w^{k-1}+\hat{w}\cdot \varphi (x^n,{\hat{y}}^n)-\hat{w}\cdot \varphi (x^n,{\tilde{y}}^n)\text{\hspace{1em}(2)} \end{gathered}$$
根据本节最开始给出的$\delta$的定义(也就是数据线性可分的假设)。
$$\begin{gathered} \hat{w}\cdot \varphi (x^1,{\hat{y}}^1)\ge \hat{w}\cdot \varphi (x^1,y)+\delta \\ \hat{w}\cdot \varphi (x^2,{\hat{y}}^2)\ge \hat{w}\cdot \varphi (x^2,y)+\delta \end{gathered}$$

公式（2）中的后面两项的差是大于等于$\delta$的
$$\hat{w}\cdot \varphi (x^n,{\hat{y}}^n)-\hat{w}\cdot \varphi (x^n,{\tilde{y}}^n)\ge \delta$$
因此公式（2）可以写为：
$$\hat{w}\cdot w^k\ge \hat{w}\cdot w^{k-1}+\delta \text{\hspace{1em}(3)}$$
算法中$w$的初始值$w^0=0$
$$\hat{w}\cdot w^1\ge \hat{w}\cdot w^0+\delta \to \hat{w}\cdot w^1\ge \delta$$
往下继续推：
$$\hat{w}\cdot w^2\ge \hat{w}\cdot w^1+\delta \to \hat{w}\cdot w^2\ge 2\delta$$
最后：
$$\hat{w}\cdot w^k\ge k\delta$$
也就是说$cos{\rho }_k$的分子是随着k的增大而增大的，但是光分子变大并不能说明夹角变小，例如：

分子变大，很可能是造成向量的长度变长，这个时候的夹角并没有变化。
因此我们还要看$cos{\rho }_k$的分母，分母中，$||\hat{w}||=1$，所以只要考虑$||w^k||$就可以，如果$||w^k||$不变，且分子变大，那么夹角就能证明是变小的拉。根据公式（1）
$$\begin{gathered} ||w^k|{|}^2=||w^{k-1}+\varphi (x^n,{\hat{y}}^n)-\varphi (x^n,{\tilde{y}}^n)|{|}^2 \\ =||w^{k-1}|{|}^2+||\varphi (x^n,{\hat{y}}^n)-\varphi (x^n,{\tilde{y}}^n)|{|}^2+2w^{k-1}\cdot (\varphi (x^n,{\hat{y}}^n)-\varphi (x^n,{\tilde{y}}^n))\text{\hspace{1em}(4)} \end{gathered}$$
公式中：
$$||\varphi (x^n,{\hat{y}}^n)-\varphi (x^n,{\tilde{y}}^n)|{|}^2>0$$
这个没啥疑问的，这个相当求距离，肯定大于0
$$2w^{k-1}\cdot (\varphi (x^n,{\hat{y}}^n)-\varphi (x^n,{\tilde{y}}^n))<0$$
这里是因为算法中规定，只有$\varphi (x^n,{\tilde{y}}^n)$比$\varphi (x^n,{\hat{y}}^n)$大才会有更新动作，这里既然是出于更新中，所以这项小于0。
假设两个特征$\varphi (x^n,{\tilde{y}}^n)$和$\varphi (x^n,{\hat{y}}^n)$的最大距离是$R$，公式（4）可以写为：
$$||w^k|{|}^2\le ||w^{k-1}|{|}^2+R^2$$
算法中$w$的初始值$w^0=0$
$$||w^1|{|}^2\le ||w^0|{|}^2+R^2\to ||w^1|{|}^2\le R^2$$
往下继续推：
$$||w^2|{|}^2\le ||w^1|{|}^2+R^2\to ||w^2|{|}^2\le 2R^2$$
最后：
$$||w^k|{|}^2\le k{R}^2$$
马上就好了，现在把我们算出来的写在一起：
$$cos{\rho }_k=\frac{\hat{w}}{||\hat{w}||}\cdot \frac{w^k}{||w^k||}\hat{w}\cdot w^k\ge k\delta ||w^k|{|}^2\le k{R}^2$$
很容易得到：
$$cos{\rho }_k=\frac{\hat{w}}{||\hat{w}||}\cdot \frac{w^k}{||w^k||}\ge \frac{k\delta }{\sqrt{k{R}^2}}=\sqrt{k}\frac{\delta }{R}$$

由于$cos$的值是小于等于1的，从图上可以看出：
$$\sqrt{k}\frac{\delta }{R}\le 1\to k\le (\frac{R}{\delta }{)}^2$$
到这里证明结束，k的上限就是$(\frac{R}{\delta }{)}^2$
最后讨论一下如何使得训练变快：

讨论

How to make training fast?不行

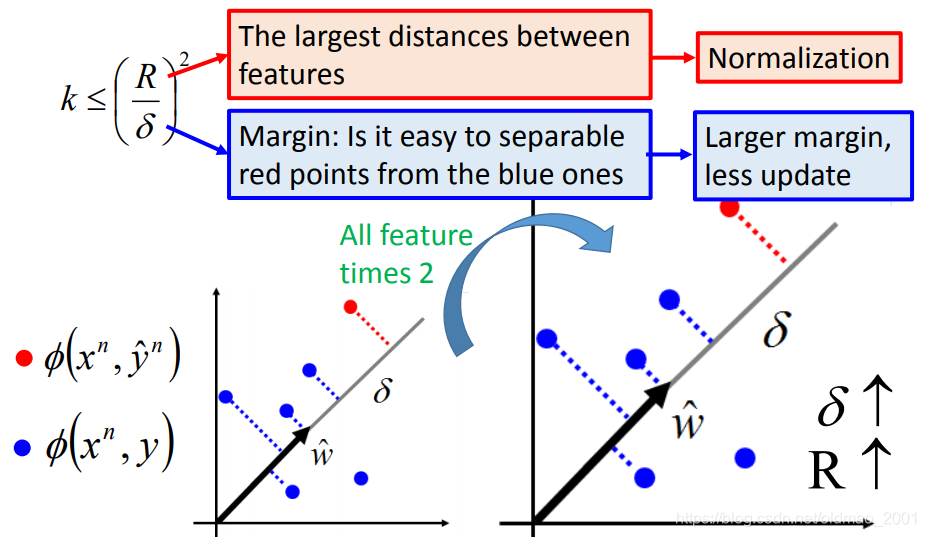
想把训练变快就是要使得k变小，使k变小就是要分母变大，或者分子变小，为了让分母变大，我们把数据都乘以2，$\delta$就变大了，但是从图上可以看出来，分子R也变大了，所以这个方法是没有用的。
当然，在实操上面线性可分的数据基本上是不可能出现的，一般都是在理论上出现，因此下面我们来看线性不可分的情况。

Non-separable case

在数据（也就是$\varphi (x,y)$）线性不可分的情况下，权重$w$仍然是可以有好坏之分的，我们可以用某些评估方法来对权重来甄别好坏，例如下图中，$w^{\prime }$比$w^{\prime \prime }$要好：

然后我们要做的是定义个衡量权重好坏的函数

Defining Cost Function

Define a cost $C$ to evaluate how bad a $w$ is, and then pick the $w$ minimizing the cost $C$
$C$ 是可以自己来定义的，老师给出一个定义：

关于$C_n$，就是第n笔数据$x^n$的cost，意思是：给定的$w$，在所有的$y$里面，找到使得$w\cdot \varphi (x^n,y)$最大的值（就是上图中最上面那个），减去正确${\hat{y}}^n$的$w\cdot \varphi (x^n,{\hat{y}}^n)$的值。
把所有的cost累加起来就是$C$
这里$C_n$最小值是0；
为什么是减去正确${\hat{y}}^n$的$w\cdot \varphi (x^n,{\hat{y}}^n)$的值，因为之前上节课的假设中我们已经假定这个值我们会算，所以顺其自然的用这个值了，如果你要用最正确的前三个值也可以，但是你不会求这三个值，会很麻烦。

(Stochastic) Gradient Descent

虽然cost函数中有一个max操作，是不可导的，但是还是可以梯度下降的，例如之前激活函数ReLU虽然在0点不可导，还不是可以反向传播。
目标是：Find $w$ minimizing the cost $C$
$$C=\sum _{n=1}^N{C}^n$$
$$C^n=arg\underset{y}{\max }[w\cdot \varphi (x^n,y)]-w\cdot \varphi (x^n,{\hat{y}}^n)$$
要求$▽C^n$，需要注意的是：When w is different, the y can be different.（意思是当$w$不一样的时候，取得第一项最大值的$y$也不一样）下面看看$w$（二维的向量）的图。
当$w$在最左边区域的时候$arg\underset{y}{\max }[w\cdot \varphi (x^n,y)]$的取值是$y^{\prime }$
当$w$在最中间区域的时候$arg\underset{y}{\max }[w\cdot \varphi (x^n,y)]$的取值是$y^{\prime \prime }$
当$w$在最右边区域的时候$arg\underset{y}{\max }[w\cdot \varphi (x^n,y)]$的取值是$y^{\prime \prime \prime }$
因此在每个区域中的$C^n$也可以很好算出来：
当$w$在最左边区域的时候$C^n=w\cdot \varphi (x^n,y^{\prime })-w\cdot \varphi (x^n,{\hat{y}}^n)$
当$w$在最中间区域的时候$C^n=w\cdot \varphi (x^n,y^{\prime \prime })-w\cdot \varphi (x^n,{\hat{y}}^n)$
当$w$在最右边区域的时候$C^n=w\cdot \varphi (x^n,y^{\prime \prime \prime })-w\cdot \varphi (x^n,{\hat{y}}^n)$
这三个区域中的边界部分不可以微分，但是在中间的区域都是可以微分的，因此，三个区域对$w$进行微分后求梯度$▽C^n$变成：
当$w$在最左边区域的时候$▽C^n=\varphi (x^n,y^{\prime })-\varphi (x^n,{\hat{y}}^n)$
当$w$在最中间区域的时候$▽C^n=\varphi (x^n,y^{\prime \prime })-\varphi (x^n,{\hat{y}}^n)$
当$w$在最右边区域的时候$▽C^n=\varphi (x^n,y^{\prime \prime \prime })-\varphi (x^n,{\hat{y}}^n)$

那么整个算法的流程如下图所示：

最后的到结果如果把学习率$\eta =1$，那么就变成了之前的 structured perceptron，减去错误加上正确的分类。

Considering Errors

看下Errors从何而来

先看看我们之前做的，实际上对于每个样本的计算，考虑的Errors都是一样的：

但是我们如果仔细看的话，会发现最下面那个其实和正确的答案已经差不多了，也就是说每个样本计算的时候Error是有所不一样的，把这些计算结果按Error进行排序（考虑错误的不同等级），就变成下面这样：

如此看来，我们希望我们找到的$w$是能够考虑Error的：

现在的问题就变成，如何考虑Error，或者说如何来衡量计算结果与正确结果之间的差距（difference）？

Defining Error Function

$△(\hat{y},y)>0$: difference between $\hat{y}$ and $y$
$A(y)$ : area of bounding box $y$
$$△(\hat{y},y)=1-\frac{A(\hat{y})\cap A(y)}{A(\hat{y})\cup A(y)}$$

考虑了Error之后，Cost函数也要改写下

Another Cost Function

从原来的：取分数最高的那个$y$减去正确的$\hat{y}$所得到的分数
$$C^n=\underset{y}{\max }[w\cdot \varphi (x^n,y)]-w\cdot \varphi (x^n,{\hat{y}}^n)$$
变成：取分数最高的那个$y$加上$\Delta$，再减去正确的$\hat{y}$所得到的分数
说人话，注意看下面的图，由于$\Delta$的存在，使得黄色框框和红色框框不像的话，分数相差越远越好，反之，黄色框框和红色框框即使是分数没有拉开也没有关系。
换句人话，$C^n$取最小值的条件是正确的$\hat{y}$的得分不但要比其他的$y$要大，而且还要大过$\Delta$才行。
$\Delta$也叫Margin
$$C^n=\underset{y}{\max }[△(\hat{y},y)+w\cdot \varphi (x^n,y)]-w\cdot \varphi (x^n,{\hat{y}}^n)$$

先看怎么来解考虑了$\Delta$的$C^n$的梯度

Gradient Descent

为了和之前没有考虑Error的梯度求解区分开来，之前用的是$\tilde{y}$，这里用$\bar{y}$，具体过程如下：
在每一个iteration，选择一个训练数据 { x n , y ^ n } \{x^n,\widehat y^n\} {xn,y ​n}
$${\bar{y}}^n=arg\underset{y}{\max }[△(\hat{y},y)+w\cdot \varphi (x^n,y)]$$
上式就是之前没有解决的Problem2，所以$△(\hat{y},y)$这个函数要选好，不然不好解决这个问题。
$$▽C^n(w)=\varphi (x^n,{\bar{y}}^n)-\varphi (x^n,{\hat{y}}^n)$$
$$w\to w-\eta [\varphi (x^n,{\bar{y}}^n)-\varphi (x^n,{\hat{y}}^n)]$$

Another Viewpoint

Minimizing the new cost function is minimizing the upper bound of the errors on training set.这里降低训练数据集中的Error上限不一定会减小Cost，只是有可能变小。
用于测试输出的函数是这个，也就是用内积最大的那个$y$当做系统输出$\tilde{y}$：$\tilde{y}=arg\underset{y}{\max }w\cdot \varphi (x^n,y)$
我们要找到一个$w$，使得系统输出的$\tilde{y}$和正确答案的$\hat{y}$的差别的累加$C^{\prime }$最小。写成：
$$C^{\prime }=\sum _{n=1}^N\Delta ({\hat{y}}^n,{\tilde{y}}^n)$$
We want to find $w$ minimizing $C^{\prime }$(和最小化errors是一样样的)
It is hard!
Because $y$ can be any kind of objects, $\Delta (\cdot ,\cdot )$ can be any function…
换个思路，找到$C^{\prime }$的上界$C$
$$C^{\prime }=\sum _{n=1}^N\Delta ({\hat{y}}^n,{\tilde{y}}^n)\le C=\sum _{n=1}^N{C}^n$$
现在要证明（从数学上证明上界这个事情）：
$$\Delta ({\hat{y}}^n,{\tilde{y}}^n)\le C^n$$
开始：
由于：
$$[w\cdot \varphi (x^n,{\tilde{y}}^n)-w\cdot \varphi (x^n,{\hat{y}}^n)]\ge 0$$
所以：
$$\Delta ({\hat{y}}^n,{\tilde{y}}^n)\le \Delta ({\hat{y}}^n,{\tilde{y}}^n)+[w\cdot \varphi (x^n,{\tilde{y}}^n)-w\cdot \varphi (x^n,{\hat{y}}^n)]$$
$$\Delta ({\hat{y}}^n,{\tilde{y}}^n)+[w\cdot \varphi (x^n,{\tilde{y}}^n)-w\cdot \varphi (x^n,{\hat{y}}^n)]=[\Delta ({\hat{y}}^n,{\tilde{y}}^n)+w\cdot \varphi (x^n,{\tilde{y}}^n)]-w\cdot \varphi (x^n,{\hat{y}}^n)$$
然后从${\tilde{y}}^n$里面可以选出一个$y$，使得：
$$[\Delta ({\hat{y}}^n,{\tilde{y}}^n)+w\cdot \varphi (x^n,{\tilde{y}}^n)]\le \underset{y}{\max }[\Delta ({\hat{y}}^n,y)+w\cdot \varphi (x^n,y)]$$
因此整理后，可得：
$$\Delta ({\hat{y}}^n,{\tilde{y}}^n)\le \underset{y}{\max }[\Delta ({\hat{y}}^n,y)+w\cdot \varphi (x^n,y)]-w\cdot \varphi (x^n,{\hat{y}}^n)=C^n$$

More Cost Functions

我们把上面的解决方案称为：Margin rescaling:
$$C^n=\underset{y}{\max }[\Delta ({\hat{y}}^n,y)+w\cdot \varphi (x^n,y)]-w\cdot \varphi (x^n,{\hat{y}}^n)$$
除了这种方法，还有别的方法，例如：
Slack variable rescaling:
$$C^n=\underset{y}{\max }\Delta ({\hat{y}}^n,y)[1+w\cdot \varphi (x^n,y)]-w\cdot \varphi (x^n,{\hat{y}}^n)]$$
这个方法的大概思想是：$y$与$\hat{y}$的差距很大，$\Delta$也就很大，乘起来之后结果会把差距放大；反之，$y$与$\hat{y}$的差距很小，$\Delta$也就很小，乘起来之后结果也会很小。
另外之前那种用的加法，有缺陷，没有考虑到$w$和$\Delta$的大小（因为$\Delta$自己定义的），例如一个是0.001，一个是1000，那么加法对这个权重上没有考虑清楚，用乘法的话就是自带normalization效果，所以这个方法有它的道理。

Regularization

Training data and testing data can have different distribution.
$w$ close to zero can minimize the influence of mismatch.
因此原有的Cost函数变成：

其中$\lambda$是调整系数，当Cost函数变成下面式子后，具体的梯度下降算法伪代码和前面差不多：
在每一个iteration，选择一个训练数据 { x n , y ^ n } \{x^n,\widehat y^n\} {xn,y ​n}
$$\bar{y}=arg\underset{y}{\max }[△(\hat{y},y)+w\cdot \varphi (x^n,y)]$$
$$▽C^n(w)=\varphi (x^n,{\bar{y}}^n)-\varphi (x^n,{\hat{y}}^n)+w$$
上式中的$w$是$\frac{1}{2}||w|{|}^2$对$w$做偏导得到的结果。
$$\begin{gathered} w\to w-\eta [\varphi (x^n,{\bar{y}}^n)-\varphi (x^n,{\hat{y}}^n)]-\eta w \\ =(1-\eta )w-\eta [\varphi (x^n,{\bar{y}}^n)-\varphi (x^n,{\hat{y}}^n)] \end{gathered}$$
前面这项就相当于DNN中的Weight Decay。

Structured SVM

把之前得到的结果写出来，然后看看Structured SVM是这么回事：

---

描述1：
Find $w$ minimizing $C$
$$C=\frac{1}{2}||w|{|}^2+\lambda \sum _{n=1}^N{C}^n$$
$$C^n=\underset{y}{\max }[\Delta ({\hat{y}}^n,y)+w\cdot \varphi (x^n,y)]-w\cdot \varphi (x^n,{\hat{y}}^n)$$

---

---

移项：
$$C^n+w\cdot \varphi (x^n,{\hat{y}}^n)=\underset{y}{\max }[\Delta ({\hat{y}}^n,y)+w\cdot \varphi (x^n,y)]\text{\hspace{1em}(1)}$$

---

说明：
$$f(x)=\underset{y}{\max }(y)\text{\hspace{1em}(a)}$$
如果 y = { 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 } y=\{1,2,3,4,5,6,7,8,9\} y={1,2,3,4,5,6,7,8,9}，那么$f(x)=9$
如果我们直接写
$$f(x)\ge \forall y\text{\hspace{1em}(b)}$$
显然(a)和(b)不等价，因为在(b)中，$f(x)$可以等于10，11，12，etc。
但是如果我们加上一个约束：$minimizef(x)$
这个时候(a)和(b)就等价了

---

根据说明，我们的目标是minimizing $C$，因此公式（1）等价下面的式子：
$$\begin{gathered} for\forall y: \\ {C}^n+w\cdot \varphi (x^n,{\hat{y}}^n)\ge \Delta ({\hat{y}}^n,y)+w\cdot \varphi (x^n,y) \end{gathered}$$
移项：
$$w\cdot \varphi (x^n,{\hat{y}}^n)-w\cdot \varphi (x^n,y)\ge \Delta ({\hat{y}}^n,y)-C^n$$
由上式可得，描述1等价于：

---

描述2：
Find $w$ minimizing $C$
$$C=\frac{1}{2}||w|{|}^2+\lambda \sum _{n=1}^N{C}^n$$
$$\begin{gathered} for\forall n: \\ for\forall y: \\ w\cdot \varphi (x^n,{\hat{y}}^n)-w\cdot \varphi (x^n,y)\ge \Delta ({\hat{y}}^n,y)-C^n \end{gathered}$$

---

到这里，通常是把$C$换成$\epsilon$（江湖人称slack variable，中文名：松弛因子），描述2等价于：

---

描述3：
Find $w,{\epsilon }^1,\cdots ,{\epsilon }^N$ minimizing $C$
$$C=\frac{1}{2}||w|{|}^2+\lambda \sum _{n=1}^N{\epsilon }^n$$
$$\begin{gathered} for\forall n: \\ for\forall y: \\ w\cdot \varphi (x^n,{\hat{y}}^n)-w\cdot \varphi (x^n,y)\ge \Delta ({\hat{y}}^n,y)-{\epsilon }^n\text{\hspace{1em}(2)} \end{gathered}$$

---

对于描述3中的公式2，如果$y={\hat{y}}^n$
那么就有：
$$\begin{gathered} w\cdot \varphi (x^n,{\hat{y}}^n)-w\cdot \varphi (x^n,y)=0 \\ \Delta ({\hat{y}}^n,y)=0 \end{gathered}$$
剩下就是：
$${\epsilon }^n\ge 0$$
描述3中的公式2就等价于：
$$\begin{gathered} For\forall y\ne {\hat{y}}^n: \\ w\cdot \varphi (x^n,{\hat{y}}^n)-w\cdot \varphi (x^n,y)\ge \Delta ({\hat{y}}^n,y)-{\epsilon }^n,{\epsilon }^n\ge 0 \end{gathered}$$
上面推导没看懂，老师贴心的给出了直观的解释：

Intuition Explanation

黄框与红框差距越大，它们之间的margin也就是$\Delta$也就越大，因此我们要找的参数$w$要满足下面的条件：

当然黄色的框框不止这两个，还有很多很多个，就是除了正确的红框之外的任意位置都可以有黄框，写成数学表达就是：$\forall y\ne \hat{y}$，所以上面的不等式也是有无穷多个。
这样我们就很难找到一个参数$w$使得所有的不等式都成立。
因此我们想办法把margin变小一点，不用$\Delta$来作为margin，而是用：$\Delta -\epsilon$来作为margin（注意，使得margin变小是要减去一个正数才可以，否则减去负数就变大了。所以这里默认$\epsilon \ge 0$，如果$\epsilon \le 0$会是使得上面的不等式约束更加严格。）：

上图中的绿色margin长度应该变小就更加逼真了。。。
由于$\epsilon$的作用是放宽约束，所以起了一个名字叫松弛因子。我们当然不会希望约束放得太宽，否则margin就失去存在的意义了（例如：$\epsilon \to \infty$，margin 就变成了负值，随便一个参数$w$就能满足条件），因此，我们还加上了一个条件就是$\epsilon$要最小化。
就好比妹子想找高富帅，这个条件没法找到，她也不会找一个矮矬穷，会想办法找一个高富，高帅，富帅。
下面举例：
假设我们有两个training data

对于$x^1$，满足下面的式子，其中红框就是${\hat{y}}^1$：

对于$x^2$，满足下面的式子，其中红框就是${\hat{y}}^2$：

根据分析，我们还希望${\epsilon }^1+{\epsilon }^2$还要最小，最后还考虑正则项，就是我们之前的描述3的内容了。

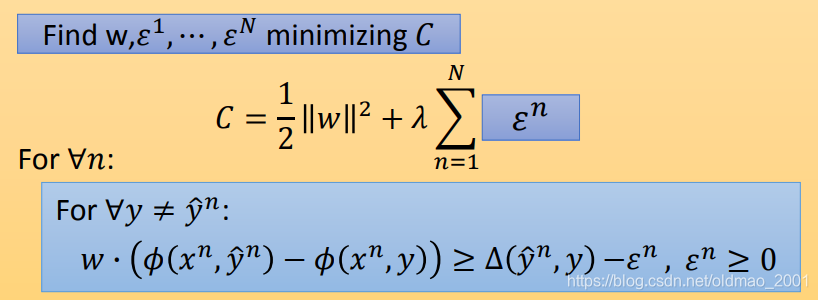
但是这个问题不好解，下面看咋弄。

Cutting Plane Algorithm for Structured SVM

问题的图形化描述

下图是参数$w,{\epsilon }^1,...,{\epsilon }^N$形成的图像，本来是高维的，这里用二维的平面来做个样例。
平面上的颜色代表了Cost $C$的值，右下角有一个绿点，那个就是还没有引入任何约束的时候的Cost $C$的最小值。

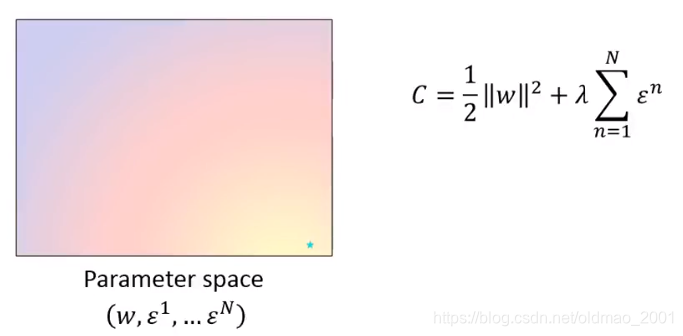
我们现在把之前推导出来的约束加上：
$$\begin{gathered} for\forall n: \\ for\forall y,y\ne \hat{y}: \\ w\cdot \varphi (x^n,{\hat{y}}^n)-w\cdot \varphi (x^n,y)\ge \Delta ({\hat{y}}^n,y)-{\epsilon }^n,{\epsilon }^n\ge 0 \end{gathered}$$
图像变成：

只有中间阴影部分是满足约束条件的，最小值也从右下角变成了上图中的位置。
中间是阴影形状是怎么来的呢？我们观察约束可以看到，虽然约束很多，但是很多约束实际上是冗余的，真正起到决定Cost最小值的是下图中的两条红线，其他约束去掉也不会影响结果：

既然不是所有约束都有用，我们就把无用的约束去掉，只留下有用的约束，并把这些有用的约束集合记为（英文名：Working set）：
$$A^n$$
则约束条件变成：
$$\begin{gathered} for\forall n: \\ fory\in A^n,y\ne \hat{y}: \\ w\cdot [\varphi (x^n,{\hat{y}}^n)-\varphi (x^n,y)]\ge \Delta ({\hat{y}}^n,y)-{\epsilon }^n,\epsilon \ge 0 \end{gathered}$$
如果Working set比较小，那么Cost最小值就是有可能解出来的，下面来看如何确定Working set，用的是一个迭代的算法。

Cutting Plane Algorithm

Elements in working set $A^n$ is selected iteratively.
对每一个example都初始化它的working set ，初始化$A^n$：$A^1,A^2,...,A^N$
根据初始化后的$A^n$，解方程
根据$A^n$，解出一个$w$后，用$w$去update$A^n$，这个过程不断循环。这个流程和EM很像。

---

Quadratic Program (QP)：凸优化的二次规划问题。

---

下面是图解这个算法如何运作的。
Initialize $A^n=null$，最开始是不考虑约束的。解出来就是蓝色星星那个点。

看看蓝色的点是没有办法满足哪些约束。例如下图中的红色约束：

虽然蓝点不满足很多约束，我们选择 the most violated one，这个选择标准后面再解释（应该是按垂直距离），先假设找出这条：

我们把找出来的这个约束记为：$y^{\prime }$，然后把$y^{\prime }$加入到working set 中：
A n = A n ∪ { y ′ } A^n=A^n\cup \{y'\} An=An∪{y′}
新的working set不再是空的了，里面有东西了，根据新的working set，我们重新算最小值：

然后再看这个蓝色星星不满足哪些约束：

我们把找出来的这个约束记为：$y^{\prime \prime }$，然后把$y^{\prime \prime }$加入到working set 中：
A n = A n ∪ { y ′ ′ } = { y ′ , y ′ ′ } A^n=A^n\cup \{y''\}=\{y',y''\} An=An∪{y′′}={y′,y′′}
下面又重复迭代，根据新的working set计算最小值

下面文字就不用写了。

Find the most violated one

上面挖了个坑，如何找到最小值相对应最不满足的约束条件是什么？现在来填：
Given $w^{\prime }$ and $\epsilon \prime$ from working sets at hand, which constraint is the most violated one?
先把约束和不满足（违反）约束的数学形式写出来：
$$\text{Constraint:}w\cdot [\varphi (x,\hat{y})-\varphi (x,y)]\ge \Delta (\hat{y},y)-\epsilon$$
$$\text{Violate a Constraint:}{w}^{\prime }\cdot [\varphi (x,\hat{y})-\varphi (x,y)]<\Delta (\hat{y},y)-{\epsilon }^{\prime }$$
在给出不满足（违反）约束的程度评价标准（上式右边减左边）：
$$\text{Degree of Violation:}\Delta (\hat{y},y)-{\epsilon }^{\prime }-w^{\prime }\cdot [\varphi (x,\hat{y})-\varphi (x,y)]$$
由于${\epsilon }^{\prime }$和$\varphi (x,\hat{y})$是固定值，不影响评价标准，所以上面式子中的这两项可以去掉：
$$\Delta (\hat{y},y)+w^{\prime }\cdot \varphi (x,y)$$
有了评价标准后，最不满足的就是最大值那个拉：
$$\text{The most violated one:}arg\underset{y}{\max }[\Delta (\hat{y},y)+w^{\prime }\cdot \varphi (x,y)]$$

算法总结

Given training data: { ( x 1 , y ^ 1 ) , ( x 2 , y ^ 2 ) , . . . , ( x N , y ^ N ) } \{(x^1,\widehat y^1),(x^2,\widehat y^2),...,(x^N,\widehat y^N)\} {(x1,y ​1),(x2,y ​2),...,(xN,y ​N)}
对每一个training data都初始一个working set：$A^1=null,A^2=null,...,A^N=null$
重复执行：

---

解决 QP with Working Set $A^1,A^2,...,A^N$，并更新$w$
QP问题如下图：

For each training data $(x^n,{\hat{y}}^n)$
$$\text{find the most violated constraints: }{\bar{y}}^n=arg\underset{y}{\max }[\Delta ({\hat{y}}^n,y)+w^{\prime }\cdot \varphi (x,y^n)]$$
把找到的最难搞的约束更新到working set：$A^n=A^n\cup {\bar{y}}^n$

---

Until $A^1,A^2,...,A^N$ doesn’t change any more（停止循环的条件）
Return $w$

图例解释

$$A^1=null,A^2=null$$

上图的约束少写了：${\epsilon }^1>0,{\epsilon }^2>0$
由于没有约束，上面那个式子很容易看出来，当$w=0$的时候，得到最小值。
然后用$w=0$去找the most violated的约束。
对于第一个training data来说
$${\bar{y}}^1=arg\underset{y}{\max }[\Delta ({\hat{y}}^1,y)+0\cdot \varphi (x,y^1)]$$
下面给出六个黄框框

由于$w=0$，后面那个没有了

只剩下$\Delta$，这个玩意如果黄框不和红框重叠，值就会很大：

看到$\Delta$有三个一样的都最大，都是1，我们随便挑一个，右下角那个作为${\bar{y}}^1$
同样去计算$y^2$对应的
$${\bar{y}}^2=arg\underset{y}{\max }[\Delta ({\hat{y}}^2,y)+0\cdot \varphi (x,y^2)]$$
然后更新working set得到：

然后用新的working set解决下图QP问题（下图中的working set中有两个约束），计算得到$w=w^1$

用$w^1$去找the most violated的约束。

对于第一个training data来说
$${\bar{y}}^1=arg\underset{y}{\max }[\Delta ({\hat{y}}^1,y)+0\cdot \varphi (x,y^1)]$$
我们用右上角那个${\bar{y}}^1=1.55$的黄色框框作为the most violated的约束
当然对第二个training data也做同样的事情，然后更新working set：

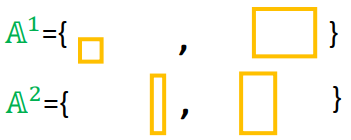
然后用新的working set解决下图QP问题（下图中的working set中有四个约束），计算得到$w=w^2$

这个过程不断迭代下去，直到 $A^1,A^2$ 不再变化为止。

---

这里有学生提问，老师又补充了一些知识，在Structured SVM的原版文章中，作者在更新working set上有一个条件，就是在the most violated的约束基础上还要加一个值，满足这个条件的约束才加入working set中，否则不加，这个值越大，整个算法的迭代次数就越少。

---

Multi-class and binary SVM

Multi-class SVM

•Problem 1: Evaluation
If there are $K$ classes, then we have K weight vectors { w 1 , w 2 , . . . , w K } \{w^1,w^2,...,w^K\} {w1,w2,...,wK}
$y$的标签自然就是：
y ∈ { 1 , 2 , . . . , k , . . . , K } y\in\{1,2,...,k,...,K\} y∈{1,2,...,k,...,K}
$$F(x,y)=w^y\cdot \overrightarrow{x}$$
$\overrightarrow{x}$：vector, representation of $x$（$x$是要分类的对象，$\overrightarrow{x}$是这个对象的向量表示）
但是之前的$F(x,y)$不是这样表示的，而是表示为：
$$F(x,y)=w\cdot \varphi (x,y)$$
那现在我们来看看这两个式子是否等价，首先$w$可以写为向量的形式，而$\varphi (x,y)$可以表示为当$x$属于第k个分类的时候，我们就把$\overrightarrow{x}$放到$\varphi (x,y)$这个向量的第k个位置。所以实际上，这两个表示是等价的。
$$w=\left[\begin{array}{c}{w}^1\\ w^2\\ ⋮\\ w^k\\ ⋮\\ w^K\end{array}\right]\varphi (x,y)=\left[\begin{array}{c}0\\ 0\\ ⋮\\ \overrightarrow{x}\\ ⋮\\ 0\end{array}\right]$$
• Problem 2: Inference
$$F(x,y)=w^y\cdot \overrightarrow{x}$$
我们就是要穷举所有的$y$找到最大那个$\hat{y}$
y ^ = a r g m a x y ∈ { 1 , 2 , . . . , k , . . . , K } F ( x , y ) = a r g m a x y ∈ { 1 , 2 , . . . , k , . . . , K } w y ⋅ x → \widehat y=arg\underset{y\in\{1,2,...,k,...,K\}}{max}F(x,y)=arg\underset{y\in\{1,2,...,k,...,K\}}{max}w^y\cdot\overrightarrow{x} y ​=argy∈{1,2,...,k,...,K}max​F(x,y)=argy∈{1,2,...,k,...,K}max​wy⋅x
The number of classes are usually small, so we can just enumerate them.
由于分类一般数量较小，所以直接硬算就可以。
• Problem 3: Training
Find $w,{\epsilon }^1,...,{\epsilon }^N$ minimizing $C$
$$C=\frac{1}{2}||w|{|}^2+\lambda \sum _{n=1}^N{\epsilon }^n$$
$For\forall n:$
$For\forall y\ne {\hat{y}}^n:$
$$w\cdot [\varphi (x^n,{\hat{y}}^n)-\varphi (x^n,y)]\ge \Delta ({\hat{y}}^n,y)-{\epsilon }^n,{\epsilon }^n\ge 0\text{\hspace{1em}(3)}$$
有$N$笔训练数据，每一个数据有$K$个分类，只有一个分类是正确的，那么由$K-1$个分类是错误的，所以我们的约束的数量就是
$$N(K-1)$$
按老师的说法，这些个约束不多，直接算即可。
根据前面的定义，我们有：
$$w\cdot \varphi (x^n,{\hat{y}}^n)=w^{{\hat{y}}^n}\cdot \overrightarrow{x},w\cdot \varphi (x^n,y)=w^y\cdot \overrightarrow{x}\text{\hspace{1em}(4)}$$
把4带入3得：
$$w^{{\hat{y}}^n}\cdot \overrightarrow{x}-w^y\cdot \overrightarrow{x}\ge \Delta ({\hat{y}}^n,y)-{\epsilon }^n,{\epsilon }^n\ge 0$$
化简：
$$(w^{{\hat{y}}^n}-w^y)\cdot \overrightarrow{x}\ge \Delta ({\hat{y}}^n,y)-{\epsilon }^n,{\epsilon }^n\ge 0$$
上式中的$\Delta ({\hat{y}}^n,y)$按之前的说法是指正确分类和错误分类的差距，这个差距是我们可以自己定义的，例如下面：
$$\begin{gathered} y\in dog,cat,bus,car \\ \Delta (\hat{y}=dog,y=cat)=1 \\ \Delta (\hat{y}=dog,y=bus)=100 \end{gathered}$$
(defined as your wish)

Binary SVM

就是多分类中的K=2的场景，这个时候 y ∈ { 1 , 2 } y\in\{1,2\} y∈{1,2}
$For\forall y\ne {\hat{y}}^n:$
$$(w^{{\hat{y}}^n}-w^y)\cdot \overrightarrow{x}\ge \Delta ({\hat{y}}^n,y)-{\epsilon }^n,{\epsilon }^n\ge 0$$
由于是二分类，我们可以定义当分类不正确的时候$\Delta ({\hat{y}}^n,y)=1$
当$y=1$的时候：
$$(w^1-w^2)\cdot \overrightarrow{x}\ge 1-{\epsilon }^n$$
当$y=2$的时候：
$$(w^2-w^1)\cdot \overrightarrow{x}\ge 1-{\epsilon }^n$$
记：$(w^1-w^2)=w$，则：
当$y=1$的时候：
$$w\cdot \overrightarrow{x}\ge 1-{\epsilon }^n$$
当$y=2$的时候：
$$-w\cdot \overrightarrow{x}\ge 1-{\epsilon }^n$$
这里就推出了二分类的SVM 的形式，感觉上面的${\epsilon }^n$应该对应到相应的上标。

Beyond Structured SVM(open question)

Structured SVM有一个很大的缺陷，就是它是linear的（怪怪的，不是说有一个核的方法来做划分平面，来解决非线性划分方法吗），而且特征的定义（就是那个$\varphi (x,y)$函数）也对结果影响很大，因此可以用DNN来自动抽取特征：

Ref: Hao Tang, Chao-hong Meng, Lin-shan Lee, “An initial attempt for phoneme recognition using Structured Support Vector Machine (SVM),” ICASSP, 2010
Shi-Xiong Zhang, Gales, M.J.F., “Structured SVMs for Automatic Speech Recognition,” in Audio, Speech, and Language Processing, IEEE Transactions on, vol.21, no.3, pp.544-555, March 2013
进一步发展，DNN和Structured SVM一起进行训练

Ref: Shi-Xiong Zhang, Chaojun Liu, Kaisheng Yao, and Yifan Gong, “DEEP NEURAL SUPPORT VECTOR MACHINES FOR SPEECH RECOGNITION”, Interspeech 2015
再进一步：

$$C=\frac{1}{2}||\theta |{|}^2+\frac{1}{2}||{\theta }^{\prime }|{|}^2+\lambda \sum _{n=1}^N{C}^n$$
$$C^n=\underset{y}{m}ax[\Delta ({\hat{y}}^n,y)+F(x^n,y)]-F(x^n,{\hat{y}}^n)$$
Ref: Yi-Hsiu Liao, Hung-yi Lee, Lin-shan Lee, “Towards Structured Deep Neural Network for Automatic Speech Recognition”, ASRU, 2015