本文深入探讨了关系图卷积网络(R-GCN)的原理与应用，R-GCN是针对知识图谱等非欧数据设计的深度学习模型，能有效处理多关系数据。文章详细解析了R-GCN的数学表达、正则项策略及其在实体分类和链接预测任务上的实验效果。
文章目录
前言
Modeling Relational Data with GraphConvolutional Networks
使用图卷积神经网络建模关系数据
作者：Michael Schlichtkrull
单位：University of Amsterdam
发表会议及时间：ESWC2018（知识图谱等语义网络的小领域的会议）
在线LaTeX公式编辑器
别人的讲解
a.非欧数据
非欧数据是生活中常见的一类数据，因为其结构化与不确定性，无法之间用grid进行表示。常见的非欧数据包括社交网络、蛋白质结构、电商网络、知识图谱等等。
b. 知识图谱
知识图谱是典型的一类非欧数据，也是目前火热的一个研究方向，熟悉常见的知识图谱，以及知识图谱可以应用到NLP中的哪些任务。
导读
非欧数据
欧式空间Euclidean domains
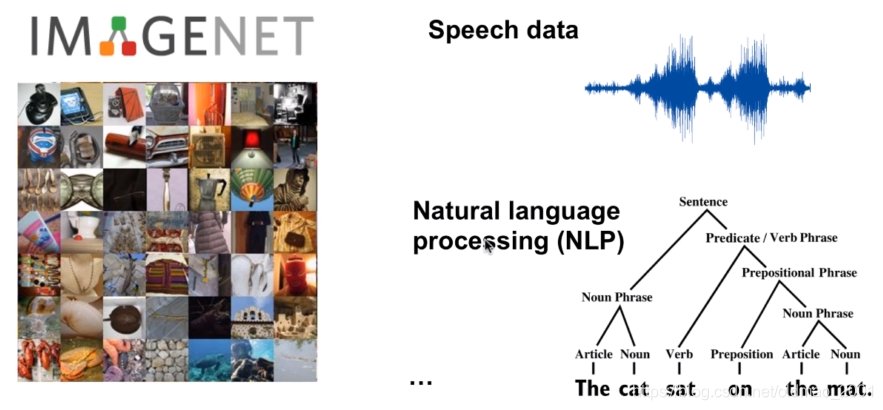
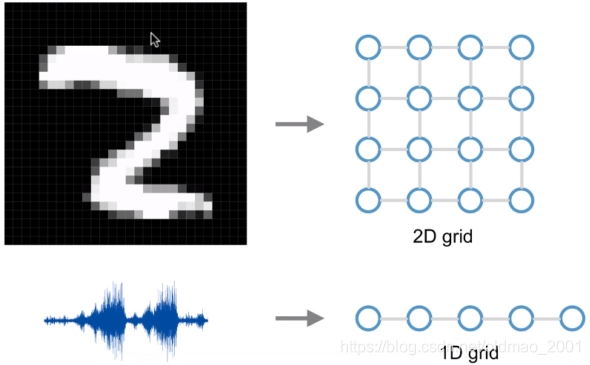
卷积神经网络很好，但是它研究的对象还是限制在Euclidean domains的数据。Euclidean data最显著的特征就是有规则的空间结构，比如图片是规则的正方形栅格，比如语音是规则的一维序列。而这些数据结构能够用一维、二维的矩阵表示，卷积神经网络处理起来很高效。
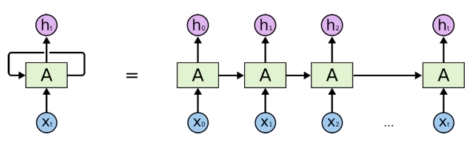
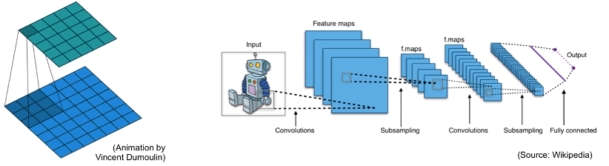
非欧数据
我们的现实生活中有很多数据并不具备规则的空间结构，称为Non Euclidean data。比如推荐系统、电子交易、计算几何、分子结构等抽象出的图谱。这些图谱结构每个节点连接都不尽相同，有的节点有三个连接，有的节点有两个连接，是不规则的数据结构。
社交网络
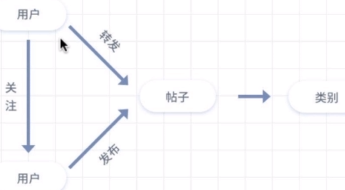
电子商务
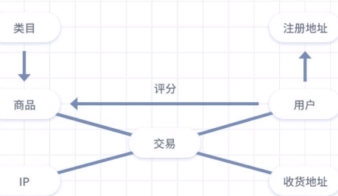
社交网风络
互联网
知识图谱
电信网络
蛋白质网络
下面左边是同质图，右边是异质图
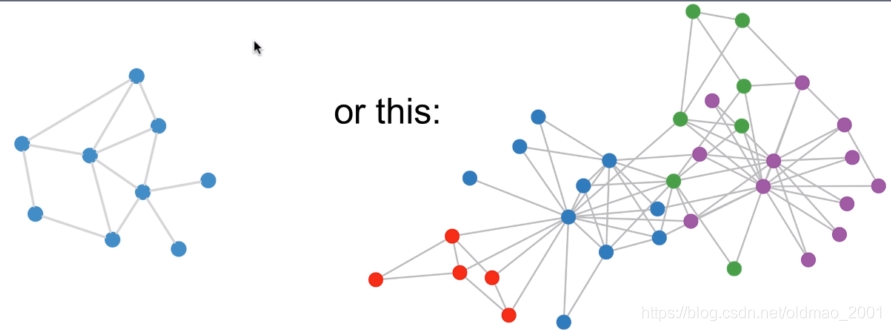
1.每个节点都有自己的特征信息
2.图谱中的每个节点还具有结构信息
图
定义：
Graph：
G
=
(
ν
,
ε
)
G=(\nu ,\varepsilon )
G=(ν,ε)
ν
\nu
ν Set of nodes
{
v
i
}
,
∣
ν
∣
=
N
\{v_i\},|\nu |= N
{vi},∣ν∣=N
ε
\varepsilon
ε Set of edges
{
v
i
,
v
j
}
\{v_i,v_j\}
{vi,vj}
A(adjacency matrix):
A
i
j
=
{
1
i
f
(
v
i
,
v
j
)
∈
ε
0
o
t
h
e
r
w
i
s
e
A_{ij}=\left\{\begin{matrix} 1\space if(v_i,v_j)\in \varepsilon\\0 \space otherwise \end{matrix}\right.
Aij={1 if(vi,vj)∈ε0 otherwise
上式中的1也可以替换为权值。
如何利用图结构？
Take adjacency matrix A and feature matrix
X
∈
R
N
×
E
X \in \mathbb{R}^{N×E}
X∈RN×E
Concatenate them
X
i
n
=
[
X
,
A
]
∈
R
N
×
(
N
+
E
)
X_{in}=[X,A]\in \mathbb{R}^{N×(N+E)}
Xin=[X,A]∈RN×(N+E)
Feed them into deep (fully connected) neural net
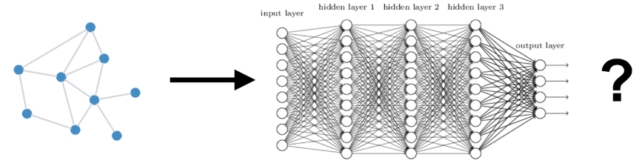
Problems:
·Huge number of parameters O(N)
·Needs to be re-trained if number of nodes changes(隐层的结点数量是等于N+E的)
·Does not generalize across graphs
知识图谱
知识就是力量
上面的非结构化文字可以用下面的结构化知识图谱来表示：
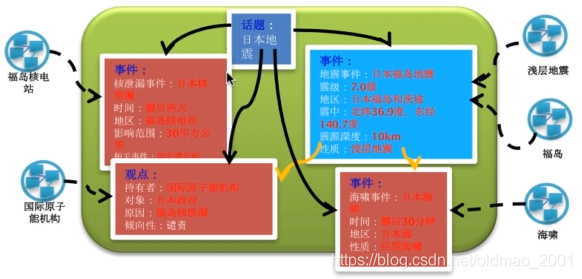
知识推理
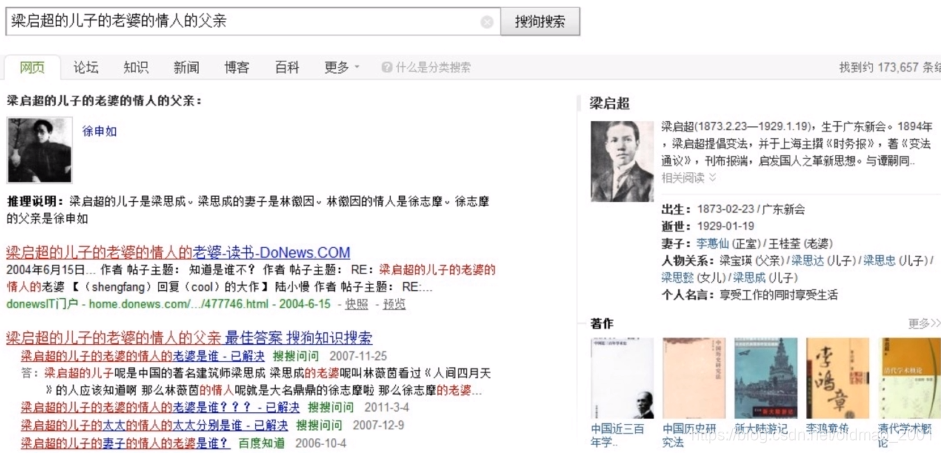
知识图谱
知识图谱本质上是一种语义网络。其结点代表实体（entity）或者概念（concept），边代表实体/概念之间的各种语义关系。
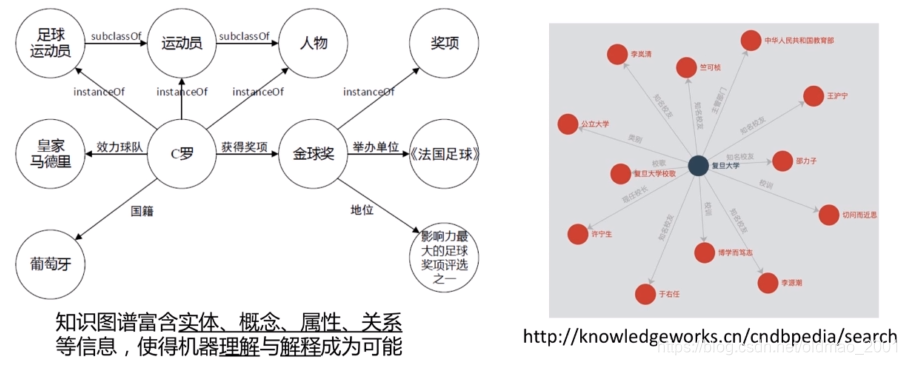
知识库是一个有向图
-多关系数据（multi-relational data）
-节点：实体/概念
-边：关系/属性
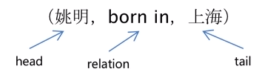
-关系事实=（head，relation，tail）
，head：头部实体
，relation：关系/属性tail：尾部实体
例如：
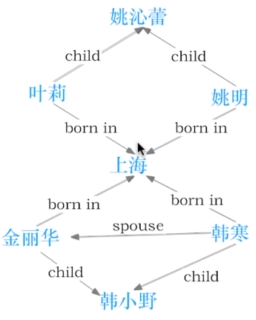
Node：值（Value）
实体（Entity）
（姚明，出生地，上海市）
字符串（String）
（北京大学，学术传统，兼容并包、思想自由）
-数字（Number）
平方公里：（北京市，面积，1.641万）
公斤：（姚明，体重，140公斤）
米：（姚明，身高，2.29米）
…
-时间（Date）
（姚明，出生年份，1981年）
-枚举（Enumerate）
（姚明，性别，男）
…
边：关系
-Subclass
-Type
-Relation
-Property、Atribute
边的例子：
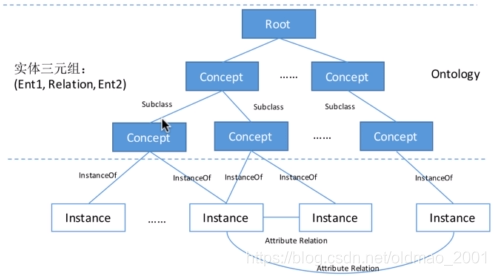
前期知识储备
非欧数据：了解实际生活中有哪些非欧数据
知识图谱：掌握知识图谱的基本概念，包括实体和关系
图卷积网络：了解图卷积神经网络
精读
GCN
动机
在第一课泛读中，提到了如果用FC来表述一个图(非欧数据)，会有很多缺陷，如何解决呢？就是用到GCN
h
i
l
+
1
=
σ
(
∑
j
∈
N
i
g
(
h
i
l
,
h
j
l
)
)
h_i^{l+1}=\sigma\left(\sum_{j\in N_i }g(h_i^l,h_j^l)\right)
hil+1=σ⎝⎛j∈Ni∑g(hil,hjl)⎠⎞
给定其中
h
i
l
h_i^l
hil是顶点
v
i
v_i
vi在第l层的特征表示，
σ
\sigma
σ表示特征激活函数例如relu，
N
i
N_i
Ni则是表示传递消息给顶点
v
i
v_i
vi的所有节点，通常是顶点
v
i
v_i
vi的入边节点。g表示聚合特征的函数，有多种表现形式。总的来说，GCN接受顶点的所有入边传递来的上一层的顶点特征消息，做相应的变换，并将其加和起来，最后通过一个激活函数作为本层的输出。实际使用中，会使用下面这种形式：
h
i
l
+
1
=
σ
(
w
0
l
h
i
l
+
∑
j
∈
N
i
1
c
i
,
j
w
1
l
h
j
l
)
(1)
h_i^{l+1}=\sigma\left(w_0^lh_i^l+\sum_{j\in N_i }\frac{1}{c_{i,j}}w_1^lh_j^l\right) \tag{1}
hil+1=σ⎝⎛w0lhil+j∈Ni∑ci,j1w1lhjl⎠⎞(1)
下面来看具体步骤：
第一步：发射（send）每一个节点将自身的特征信息经过变换后发送给邻居节点。这一步是在对节点的特征信息进行抽取变换。视频里面是动图，这里没法展示，就是每个结点会把自己的信息发射出去。
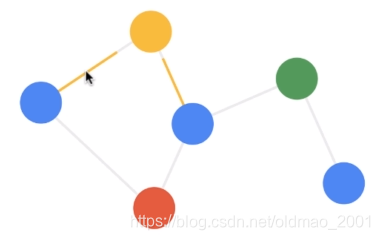
第二步：接收（receive）每个节点将邻居节点的特征信息聚集起来。这一步是在对节点的局部结构信息进行融合。就是上面公式1中的加和操作（对所有的邻居结点）。
第三步：变换（transform）把前面的信息聚集之后做非线性变换，增加模型的表达能力。注意：图结构不变，变的是结点的特征
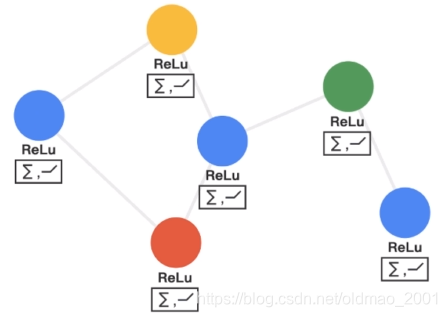
GCN具有卷积神经网络的以下性质：
1.局部参数共享，算子是适用于每个节点（圆圈代表算子），处处共享。指的是公式中的
w
0
和
w
1
w_0和w_1
w0和w1
2.感受域正比于层数，最开始的时候，每个节点包含了直接邻居的信息，再计算第二层时就能把邻居的邻居的信息包含进来，这样参与运算的信息就更多更充分。层数越多，感受域就更广，参与运算的信息就更多。
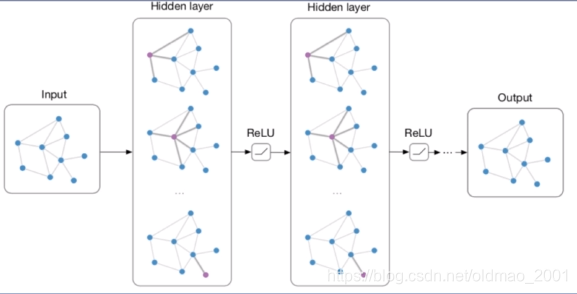
GCN模型同样具备深度学习的三种性质：
1.层级结构（特征一层一层抽取，一层比一层更抽象，更高级）
2.非线性变换（增加模型的表达能力）
3.端对端训练（不需要再去定义任何规则，只需要给图的节点一个标记，让模型自己学习，融合特征信息和结构信息。）
R-GCN
模型
R-GCN
h
i
l
+
1
=
σ
(
w
0
l
h
i
l
+
∑
r
∈
R
∑
j
∈
N
i
r
1
c
i
,
j
w
r
l
h
j
l
)
(2)
h_i^{l+1}=\sigma\left(w_0^lh_i^l+\sum_{r\in R}\sum_{j\in N_i^r }\frac{1}{c_{i,j}}w_r^lh_j^l\right)\tag{2}
hil+1=σ⎝⎛w0lhil+r∈R∑j∈Nir∑ci,j1wrlhjl⎠⎞(2)
和GCN公式1对比，右边部分对于结点本身
w
0
l
h
i
l
w_0^lh_i^l
w0lhil的计算是一样的。不同是R-GCN对于不同类型的边加入了不同的权重矩阵，换句话说R-GCN把边的权重考虑到计算中来了。但是，为每一条边加上权重矩阵
w
r
l
w_r^l
wrl（每一个边代表一种关系，每一个关系加一个权重）会导致巨大的参数量，会导致过拟合。解决方法就是：减少参数量（使用基分解、对角块分解），具体就是正则项
给定其中
h
i
l
h_i^l
hil是顶点
v
i
v_i
vi在第l层的特征表示，
σ
\sigma
σ表示特征激活函数例如relu，
N
i
r
N_i^r
Nir是表示和
v
i
v_i
vi相连且关系为r的所有节点，R是边的关系集合。
总的来说，GCN接受顶点的所有入边传递来的上一层的顶点特征消息并根据边的关系不同做相应的变换，并将其加和起来，最后通过一个激活函数作为本层的输出。
正则项
基分解：
W
r
l
=
∑
b
=
1
B
a
r
,
b
l
V
b
l
W_r^l=\sum_{b=1}^Ba_{r,b}^lV_b^l
Wrl=∑b=1Bar,blVbl
W
r
l
W_r^l
Wrl被认为是基变换（向量）
V
b
l
V_b^l
Vbl与系数
a
r
,
b
l
a_{r,b}^l
ar,bl的线性组合，且仅和关系r相关。这个东西的思想是权值可以看做是一个基础矩阵（这个部分是共享的）与向量（这个部分是特有的，这个向量有b个数）相乘的结果，这样就把很多复杂参数简化为了很多简单向量。
块对角分解：
W
r
l
=
d
i
a
g
(
Q
1
,
r
l
,
.
.
.
,
Q
B
,
r
l
)
Q
B
,
r
l
∈
R
d
l
+
1
B
×
d
l
B
W_r^l=diag(Q_{1,r}^l,...,Q_{B,r}^l) \space Q_{B,r}^l\in \mathbb{R}^{\frac{d^{l+1}}{B}×\frac{d^l}{B}}
Wrl=diag(Q1,rl,...,QB,rl) QB,rl∈RBdl+1×Bdl
这个方法的思想是把权重矩阵中转换为对角线矩阵，非对角线带的位置都置为0.
基函数分解可以看作是不同关系类型之间权重有效共享的一种形式，而块分解可以看作是每个关系类型的权重矩阵上的稀疏性约束。两种分解都减少了拟合多关系数据所需的参数数量。同时，可以减轻对长尾关系的过度拟合，因为参数的更新在长尾关系和频繁关系之间是共享的。
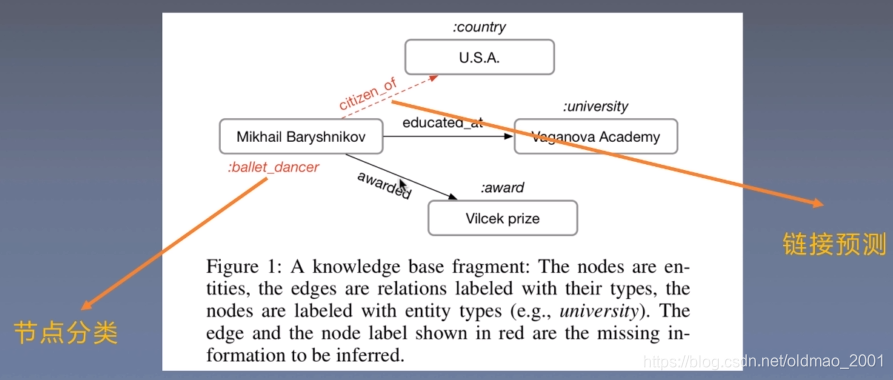
实体分类
给定结点，得到结点类型
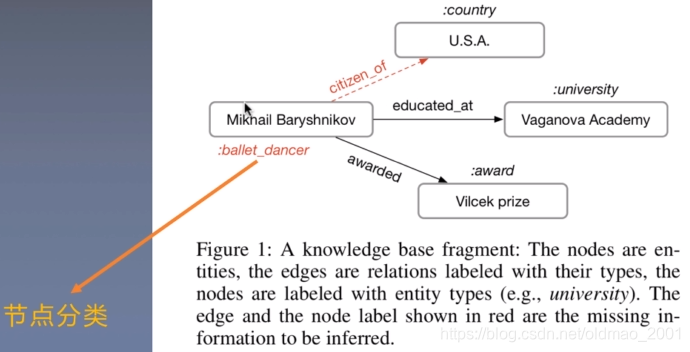
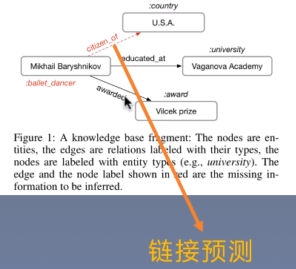
链接预测
根据实体分类得到s和o，然后判断s和o之间的关系是r的概率，即
（s，r，0）三元组—>f（s，r，o）三元组成立概率
具体上是用s的向量表示的转置乘上关系矩阵乘上o的向量表示，最后得到一个得分
f
(
s
,
r
,
o
)
=
e
s
T
R
r
e
o
f(s,r,o)=e_s^TR_re_o
f(s,r,o)=esTRreo
然后用下面的损失函数去学习关系的向量矩阵。
l
=
∑
(
s
,
r
,
o
,
y
)
∈
ζ
y
l
o
g
s
i
g
m
o
i
d
(
f
(
s
,
r
,
o
)
)
+
(
1
−
y
)
l
o
g
(
1
−
s
i
g
m
o
i
d
(
f
(
s
,
r
,
o
)
)
)
l=\sum_{(s,r,o,y)\in\zeta}ylogsigmoid(f(s,r,o))+(1-y)log(1-sigmoid(f(s,r,o)))
l=(s,r,o,y)∈ζ∑ylogsigmoid(f(s,r,o))+(1−y)log(1−sigmoid(f(s,r,o)))
实验结果
实体分类
有两个数据集结果不是很好，论文里面有讲why
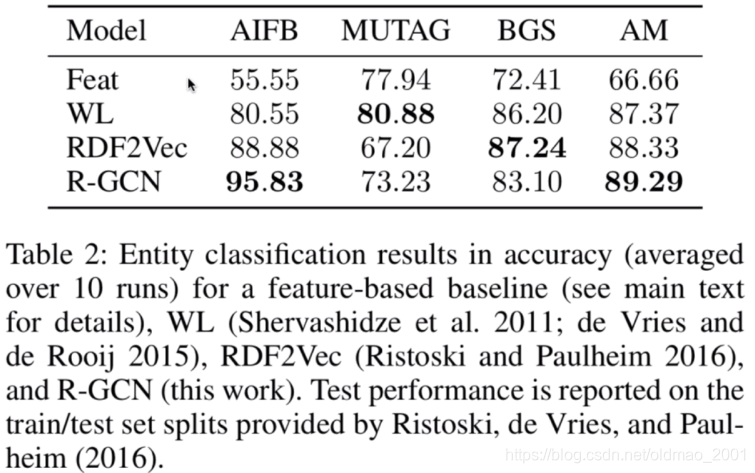
链接预测
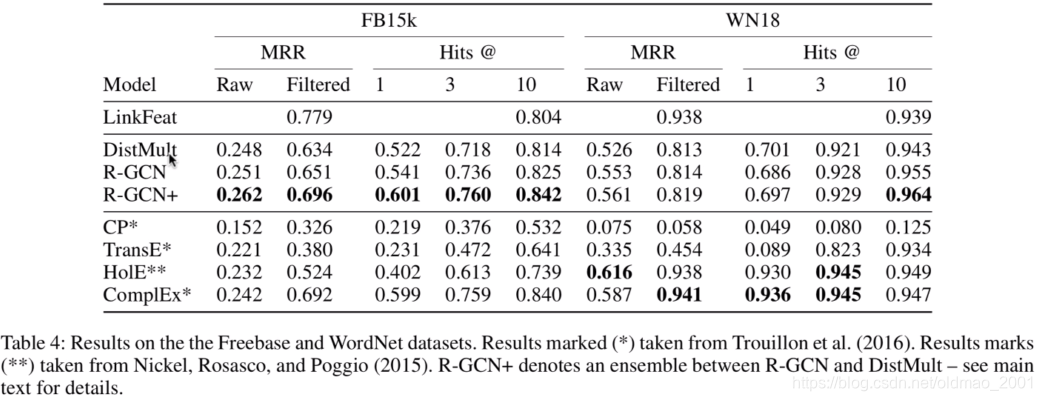
讨论和总结
A.提出一种面向关系图的图卷积
1.考虑关系类型对特征矩阵的影响
2.使用分解策略减少参数量
B.在实体分类和链接预测任务上验证了有效性
C.对后续工作有很大启发
实验分析十分详尽
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
