面试题27：二叉排序树转换成有序双向链表

题目描述：将二叉排序树转换成一个排序的双向链表，要求：不能创建任何新的节点，只能通过调整指针的指向来实现；

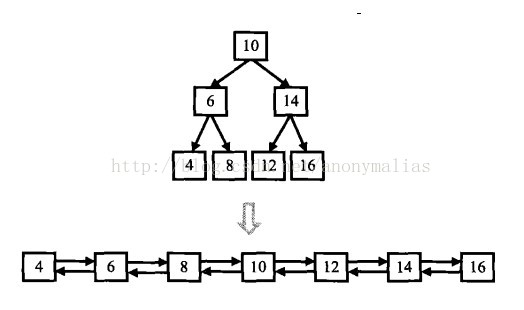
二叉排序树的一个很重要的特性就是：二叉树中序遍历的结果是一个递增的序列。由这个特性可以知道该题需要通过中序遍历的思想来解决。

一.简单直观的解法

可以看到上述序列是二叉树的中序遍历的结果，我们可以：

1. 用vector保存二叉树中序遍历的结果
2. 从头到尾调整指针，前一个节点的right指向后一个节点，后一个节点的left指向前一个节点
3. 返回vector的第一个元素，就是双链表的头节点。
   代码如下：

TreeNode* Convert(TreeNode* pRootOfTree)
{
  if (pRootOfTree == nullptr) {
    return pRootOfTree;
  }

  vector<TreeNode*> result;
  MidTravel(pRootOfTree, &result);
  
  int size = result.size();
  TreeNode* pre = nullptr;
  TreeNode* next = nullptr;
  for (int i = 0; i < size-1; ++i) {
    pre = result[i];
    next = result[i+1];
    pre->right = next;
    next->left = pre;
  }
  return result[0];
}

void MidTravel(TreeNode* root, vector<TreeNode*>* result) {
  if (root == nullptr) {
    return;
  }
  MidTravel(root->left, result);
  result->push_back(root);
  MidTravel(root->right, result);
}

二. 不需要额外空间的解法

• 按照中序遍历的递归思路，先遍历左子树，然后处理根节点，最后遍历右子树。关键的步骤在于处理根节点。

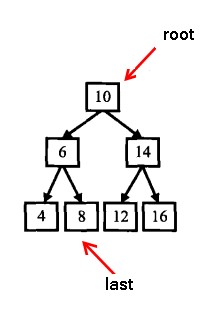
如下图所示，我们通过中序递归遍历过程中的一个状态来解析转换的过程，当中序遍历root指向10时，要满足转换成双向有序链表的请求，结点10左指针必须指向它中序遍历的前一个结点8，而前一个结点8的右指针必须指向结点10。

• 设置一个初始的last节点，假设它是双链表的最后一个节点。root的left指向last，last的right指向root，最后用root代替原来的last，root就成了双向链表的最后一个节点

代码如下：

root->left = last;
last->right = root;
last = root;

生成的双链表，前驱指针是left，后接指针是right。

这样才能把这两个结点双向连接起来，转换完成后，需要找到双向链表的头节点，也就是最左边的叶子节点。
下面是详细的实现代码：

//结点的结构
struct BSTNode{
    int data;
    BSTNode *left;
    BSTNode *right;
};

//主函数
BSTNode* Convert2DoubleLinkList(BSTNode *root)
{
    if(root == NULL)    
        return NULL;
    
    BSTNode *last = NULL;
    
    //二叉排序树转换成排序双向链表
    Convert(root, &last);

    //取得双向链表的头指针
    while(root->left != NULL)
        root = root->left;

    return root;
}

//二叉排序树转换成双向链表
void Convert(BSTNode *root, BSTNode** last)
{
    if(root == NULL)
        return;
	
	//遍历左子树
    Convert(root->left, last);

	//处理根节点
    root->left = *last;
    if((*last) != NULL)
        (*last)->right = root;
    *last = root;
	
	//遍历右子树
    Convert(root->right, last);
}