数据结构与算法-二叉树-简单实现

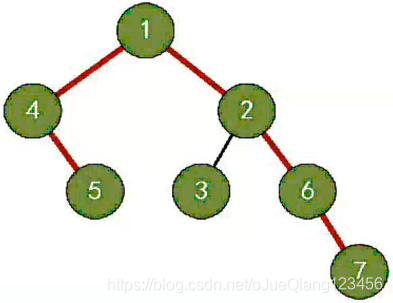
一、概述

• Node (结点类)
• BinaryTree (接口类)
• LinkBinaryTree (链表实现的二叉树类)
• Test (测试类)

二、代码

Node：

public class Node {

	/** 内容 **/
	private Object data;
	/** 左子树 **/
	private Node leftChild;
	/** 右子树 **/
	private Node rightChild;
	
	public Node() {
		super();
	}
	
	public Node(Object data, Node leftChild, Node rightChild) {
		super();
		this.data = data;
		this.leftChild = leftChild;
		this.rightChild = rightChild;
	}

	public Object getData() {
		return data;
	}
	public void setData(Object data) {
		this.data = data;
	}
	public Node getLeftChild() {
		return leftChild;
	}
	public void setLeftChild(Node leftChild) {
		this.leftChild = leftChild;
	}
	public Node getRightChild() {
		return rightChild;
	}
	public void setRightChild(Node rightChild) {
		this.rightChild = rightChild;
	}

	@Override
	public String toString() {
		return "Node [data=" + data + ", leftChild=" + leftChild + ", rightChild=" + rightChild + "]";
	}
}

BinaryTree：

public interface BinaryTree {

	/**
	 * 是否为空树
	 * @return
	 */
	public boolean isEmpty();
	
	/**
	 * 先序遍历(递归)
	 */
	public void preOrderTraverse();
	
	/**
	 * 中序遍历(递归)
	 */
	public void inOrderTraverse();

	/**
	 * 中序遍历(栈)
	 */
	public void inOrderStack();
	
	/**
	 * 后序遍历(递归)
	 */
	public void postOrderTraverse();
	
	/**
	 * 按层次遍历
	 */
	public void levelOrderStark();
	
	/**
	 * 获取树的高度
	 * @return
	 */
	public int getHeight();
	
	/**
	 * 获取树的元素个数
	 * @return
	 */
	public int getSize();
	
	/**
	 * 查找值
	 * @param obj
	 * @return
	 */
	public Node findKey(Object obj);
}

LinkBinaryTree：

public class LinkBinaryTree implements BinaryTree {

	/** 根结点 **/
	private Node root;
	
	/**
	 * 是否为空树
	 */
	public boolean isEmpty() {
		return root == null;
	}
	
	/**
	 * 先序遍历(递归)
	 */
	public void preOrderTraverse() {
		System.out.println("先序遍历(递归) 开始");
		this.inPreOrderTraverse(this.root);
		System.out.println("\n先序遍历(递归) 结束");
	}
	public void inPreOrderTraverse(Node node) {
		if(null != node) {
			// 输出根结点的值
			System.out.print(node.getData() + " ");
			// 左子树先序遍历
			this.inPreOrderTraverse(node.getLeftChild());
			// 右子树先序遍历
			this.inPreOrderTraverse(node.getRightChild());
		}
	}
	
	/**
	 * 中序遍历(递归)
	 */
	public void inOrderTraverse() {
		System.out.println("中序遍历(递归) 开始");
		this.inInOrderTraverse(this.root);
		System.out.println("\n中序遍历(递归) 结束");
	}
	public void inInOrderTraverse(Node node) {
		if(null != node) {
			// 左子树先序遍历
			this.inInOrderTraverse(node.getLeftChild());
			// 输出根结点的值
			System.out.print(node.getData() + " ");
			// 右子树先序遍历
			this.inInOrderTraverse(node.getRightChild());
		}
	}
	
	/**
	 * 中序遍历(栈)
	 */
	public void inOrderStack() {
		System.out.println("中序遍历(栈) 开始");
		Deque<Node> deque = new LinkedList<Node>();
		Node node = this.root;
		while (null != node || !deque.isEmpty()) {
			while (null != node) {
				deque.push(node);
				node = node.getLeftChild();
			}
			if(!deque.isEmpty()) {
				Node popNode = deque.pop();
				System.out.print(popNode.getData());
				node = popNode.getRightChild();
			}
		}
		System.out.println("\n中序遍历(栈) 结束");
	}
	
	/**
	 * 后序遍历(递归)
	 */
	public void postOrderTraverse() {
		System.out.println("后序遍历(递归) 开始");
		this.inPostOrderTraverse(this.root);
		System.out.println("\n后序遍历(递归) 结束");
	}
	public void inPostOrderTraverse(Node node) {
		if(null != node) {
			// 左子树先序遍历
			this.inPostOrderTraverse(node.getLeftChild());
			// 右子树先序遍历
			this.inPostOrderTraverse(node.getRightChild());
			// 输出根结点的值
			System.out.print(node.getData() + " ");
		}
	}
	
	/**
	 * 按层次遍历
	 */
	public void levelOrderStark() {
		System.out.println("按层次遍历(队列) 开始");
		this.inLevelOrderStark(this.root);
		System.out.println("\n按层次遍历(队列) 开始");
	}
	public void inLevelOrderStark(Node node) {
		if(null != node) {
			Queue<Node> queue = new LinkedList<Node>();
			queue.add(node);
			while (queue.size() > 0) {
				int len = queue.size();
				for (int i = 0; i < len; i++) {
					Node popNode = queue.poll();
					System.out.print(popNode.getData() + " ");
					if(null != popNode.getLeftChild()) {
						queue.add(popNode.getLeftChild());
					}
					if(null != popNode.getRightChild()) {
						queue.add(popNode.getRightChild());
					}
				}
			}
		}
	}
	
	/**
	 * 获取树的高度
	 */
	public int getHeight() {
		return this.inGetHeight(this.root);
	}
	public int inGetHeight(Node node) {
		if(null == node) {
			return 0;
		} else {
			// 左子树高度
			int i = inGetHeight(node.getLeftChild());
			// 右子树高度
			int j = inGetHeight(node.getRightChild());
			return i > j ? (i+1) : (j+1);
		}
	}
	
	public int getSize() {
		return this.inGetSize(this.root);
	}
	public int inGetSize(Node node) {
		if(null == node) {
			return 0;
		} else {
			// 左子树元素
			int i = inGetSize(node.getLeftChild());
			// 右子树元素
			int j = inGetSize(node.getRightChild());
			return i+j+1;
		}
	}
	
	/**
	 * 查找值
	 */
	public Node findKey(Object obj) {
		return inFindKey(this.root, obj);
	}
	public Node inFindKey(Node node, Object obj) {
		if(null == node || null == obj) {
			return null;
		}
		if(node.getData() == obj) {
			return node;
		}
		Node leftNode = this.inFindKey(node.getLeftChild(), obj);
		Node rightNode = this.inFindKey(node.getRightChild(), obj);
		if(leftNode != null && leftNode.getData() == obj) {
			return leftNode;
		}
		if(rightNode != null && rightNode.getData() == obj) {
			return rightNode;
		}
		return null;
	}
	
	public LinkBinaryTree() {
		super();
	}
	public LinkBinaryTree(Node root) {
		super();
		this.root = root;
	}
	public Node getRoot() {
		return root;
	}
	public void setRoot(Node root) {
		this.root = root;
	}
}

Test：

public class Test {
	public static void main(String[] args) {
		// 左子树
		Node node5 = new Node(5, null, null);
		Node node4 = new Node(4, null, node5);
		// 右子树
		Node node7 = new Node(7, null, null);
		Node node6 = new Node(6, null, node7);
		Node node3 = new Node(3, null, null);
		Node node2 = new Node(2, node3, node6);
		// 根
		Node node1 = new Node(1, node4, node2);
		
		BinaryTree binaryTree = new LinkBinaryTree(node1);
		
		// 树是否为空
		System.out.println(binaryTree.isEmpty());
		
		// 先序遍历(递归)
		binaryTree.preOrderTraverse();
		
		// 中序遍历(递归)
		binaryTree.inOrderTraverse();
		// 中序遍历(栈)
		binaryTree.inOrderStack();
		
		// 查找某个值
		System.out.println("查号某个值：" + binaryTree.findKey(7));
		
		// 按层次遍历(队列)
		binaryTree.levelOrderStark();
		
		// 后序遍历(递归)
		binaryTree.postOrderTraverse();
		
		// 获取树的高度
		System.out.println("树的高度：" + binaryTree.getHeight());
		
		// 获取树的元素个数
		System.out.println("树元素的个数：" + binaryTree.getSize());
	}
}