你好，我是B树

一、什么是B树？

灵槐小说网 https://www.2962.info

B树是一棵是具备以下特点的有根树。

1、节点属性

a）x.n：为节点中存储的关键字个数。

b）x.key：为节点中存储的关键字。x.key₁、x.key₂ ... x.key_x.n 以非降序顺序排列，满足 x.key₁ <= x.key₂ ... <= x.key_x.n。

c）x.leaf：为当前节点是否为叶子节点（true | false）

d）x.c：为指向子节点的指针，内部节点包含指针个数为 x.n + 1，叶子节点没有子节点，所以没有此属性。

2、分割

关键字 x.key 对存储在子树中的关键字进行分割。某个子节点的所有关键字值范围总是在节点 x 的某两个关键字之间。这个值可能是任何可排序的表示，比如：

3、深度

每个叶子节点具有相同的深度，即树的高度（由根节点到叶子节点的路径长度）。

4、度数

每个节点包含的关键字个数有上下界限制。基本表示单位为B树的最小度数 t（满足 t >= 2）：

a）除了根节点外（空树没有关键字，非空树根节点至少包含一个关键字），每个节点至少有 t - 1 个关键字，进而可以推导，每个内部节点至少有 t 个子节点【1.d】。

b）每个节点至多包含 2t - 1 个关键字（此时称之为【满】 状态），进而可以推导，每个内部节点至多有 2t 个子节点【1.d】。

二、B数的高度

首先树的根节点至少包含 1 个关键字，其它节点至少包含 t - 1 个关键字，至少有 t 个子节点【一.4.a】。

我们知道 B 树的度数 t >= 2，所以：

深度为 1 的位置上至少有 2 个节点。

深度为 2 的位置至少有 2 * t 个 节点。

深度为 3 的位置至少有 2 * t * t 个 节点。

... ...

深度为 h 的位置至少有 2 * t * ... * t 个 节点。

图示：

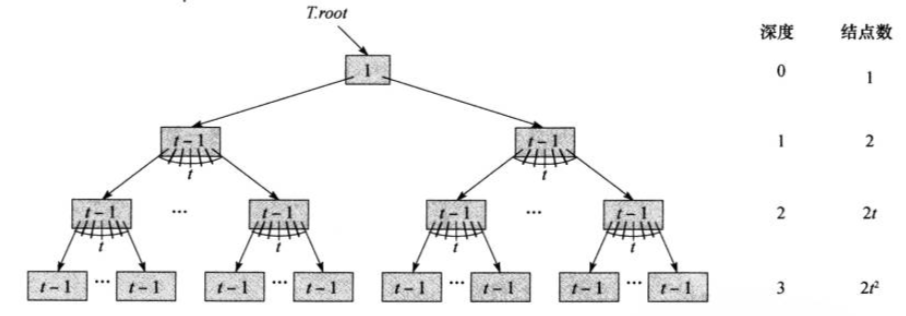
【1】所以所有非根节点个数至少为：2 + 2 * t +  2 * t * t  + 2 * t * ... * t = 2 * t⁰ + 2 * t¹+  2 * t²  + 2 * t^h-1，标识为 sum(node)

【2】相应的非根节点关键字个数至少为：(t - 1) * sum(node)

【3】那么总的关键字个数至少为： 1 + (t - 1) * sum(node)

【4】我们用 n 表示关键字个数，所以存在  n >= 1 + (t - 1) * sum(node)，代入【1】中的求和，最终经过一系列的变换，可以得出B树的高度满足：h <= log_t(n+1)/2。

三、B树的搜索

假定我们要查找的关键字为 k，入口节点 x：

a）需要找到 k 在 x 所有关键字中的位置，临界关键字 key_i 满足 k <= key_i 。

b）如果存在 k == key_i 那么查找结束，否则继续。

c）如果 x 为叶子节点，则查找结束，否则继续

d）由 key_i 临界关键字，我们可以得到相应指向子节点的指针 c_i。

然后，继续由 c_i 指向的子节点作为入口节点，继续上述过程。

四、B树的插入

B树插入新关键字后，必须仍然是一颗合法的B树。

由【一.4.b】我们直到 B 树节点存在一种状态【满】，即当前节点关键字个数为 2t -1。【满】状态的节点插入新节点必须经过特定的前置处理：分裂。

所谓分裂，即将节点由中间关键字作为分割点，分割为两个节点，每个节点包含 t - 1 个关键字，中间节点 x.k_t 则上升到父节点中，作为两棵子树的划分点，参见【一.2】。

此处需要注意的是，如果父节点同样为【满】节点，那么在分割点上升之前，同样需要对父节点执行【分裂】操作。

满节点的分裂行为会沿着树向上传播直到不再需要分裂为止。

上面我们描述的过程，是一个自下而上的【满】状态分裂传播行为。

我们知道，要实现节点的插入，首先需要经过一个B树的搜索查找的过程，搜索过程自上而下。

显然，两个过程，有些重复，我们需要的是单向查找插入。

鉴于此，在执行查找的过程中，遇到路径上的满节点，则执行分裂操作，直到找到位置插入节点，这样就避免了自下而上的【分裂】传播行为。

五、B树的删除

B树删除特定关键字后，必须仍然是一颗合法的B树。

B树的插入是一个对节点最大关键字数量的约束满足过程，相应的，B树的删除是一个对节点最小关键字数量的约束满足过程。

保障沿途节点关键字数量至少为度数 t，一遍自根而下执行删除。