置换检验

一、置换检验

显著性检验通常可以告诉我们一个观测值是否是有效的，例如检测两组样本均值差异的假设检验可以告诉我们这两组样本的均值是否相等（或者那个均值更大）。我们在实验中经常会因为各种问题（时间、经费、人力、物力）得到一些小样本结果，如果我们想知道这些小样本结果的总体是什么样子的，就需要用到置换检验。

Permutation test 置换检验是Fisher于20世纪30年代提出的一种基于大量计算（computationally intensive），利用样本数据的全（或随机）排列，进行统计推断的方法，因其对总体分布自由，应用较为广泛，特别适用于总体分布未知的小样本资料，以及某些难以用常规方法分析资料的假设检验问题。与Bootstrap 类似，通过对样本进行顺序上的置换，重新计算统计检验量，构造经验分布，然后在此基础上求出P-value进行推断。

二、置换检验基本思想

下面我们考虑两样本的均值比较问题来阐释置换检验的基本思想。

假设 （X₁, …, X_n）和（Y₁, … , Y_m）分别来自分布F和G，现检验（原假设）：

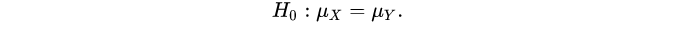
对此，我们将统计量定义为：

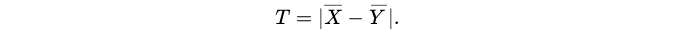
在原假设下，T应较小（甚至接近于0）；在备择假设下，T应较大。

那么多大算大呢（显著）？也就是临界值如何确定呢？

对此，我们应设法寻求统计量T在原假设下的分布。

• 若 F 和 G 是同方差的正态分布，则 T 可修正为Student’s t统计量。
• 若正态假定不成立，又该如何操作呢？一种方法是依赖于中心极限定理确定 T 的渐近分布，而另一种方法则可考虑Bootstrap近似。但需明确的是，在样本量很小时，不论渐近分布还是Bootstrap近似都不是统计量精确分布的较好近似。

这就引出一个重要的问题：在样本量很小且分布未知时，能否确定统计量 T 在原假设下的临界值呢？

Fisher给出了肯定的答案：Permutation！

所谓Permutation或者置换也就是重新洗牌或者排列。

1. 我们把两组数据（X₁, …, X_n）和（Y₁, … , Y_m）合并在一起，得到Z = (Z₁, … , Z_N) = (X₁, …, X_n, Y₁, … , Y_m)，这里N = n + m。
2. 然后将Z进行全排列，全排列的前 n 个数构成新的 （X₁^*, …, X_n^*），余下的m个数据则构成新的（Y₁^*, …, Y_m^*）。
3. 基于此，计算置换后的统计量T^* = |mean(X^*)-mean(Y^*)|。共有N!个全排列，故得到N!个T_i^*, i = 1, …, N!。
4. 在原假设下，（X₁, …, X_n）和（Y₁, … , Y_m）来自同一分布，故每一个 T_i^* 的取值都是等可能的。由此可用 T_i^* 的经验分位数来作为临界值。

根据经验分布依据的数据是否为所有可能的排列组合，可进一步将置换检验分为以下两种：

• 精确检验：经验分布依据的数据为所有可能的排列组合，样本量的增加，获取所有可能排列的时间开销会非常大。
• 蒙特卡洛模拟：从所有可能的排列中进行抽样，获得一个近似的检验。

三、应用

1. 简单小样本置换检验

考虑关于玩具的例子，假设数据（X₁， X₂， Y₁）= （1， 9， 3），令T = |mean(X) - mean(Y)|。对此数据，传统的t检验和Bootstrap方法都是无法操作的，而置换检验却可以得到精确的p值。

p值为P(T > t_obs=2)，故不能认为两组数据的均值不同。自然这个结论主要是因为样本量实在太少了。

2. 简单例子

假设我们设计了一个实验来验证加入某种生长素后拟南芥的侧根数量会明显增加。A组是加入某种生长素后，拟南芥的侧根数量；B是不加生长素时，拟南芥的侧根数量（均为假定值）。

• A组侧根数量（共12个数据）：24 43 58 67 61 44 67 49 59 52 62 50
• B组侧根数量（共16个数据）：42 43 65 26 33 41 19 54 42 20 17 60 37 42 55 28

我们来用假设检验的方法来判断生长素是否起作用。我们的零假设为：加入的生长素不会促进拟南芥的根系发育。在这个检验中，若零假设成立，那么A组数据的分布和B组数据的分布是一样的，也就是服从同个分布。

接下来构造检验统计量——A组侧根数目的均值同B组侧根数目的均值之差。

• statistic:= mean(Xa)-mean(Xb)

对于观测值有 Sobs:=mean(Xa)-mean(Xb)=(24+43+58+67+61+44+67+49+59+52+62+50)/12-(42+43+65+26+33+41+19+54+42+20+17+60+37+42+55+28)/16=14

我们可以通过Sobs在置换分布（permutation distribution）中的位置来得到它的P-value。

Permutation test的具体步骤是：

1. 将A、B两组数据合并到一个集合中，从中挑选出12个作为A组的数据（X’a），剩下的作为B组的数据（X’b）。
   Gourp:=24 43 58 67 61 44 67 49 59 52 62 50 42 43 65 26 33 41 19 54 42 20 17 60 37 42 55 28
   • 挑选出 X’a:=43 17 44 62 60 26 28 61 50 43 33 19
   • X’b:=55 41 42 65 59 24 54 52 42 49 37 67 67 20 42 582
2. 计算并记录第一步中A组同B组的均值之差。Sper:=mean(X’a)-mean(X’b)= -7.8753.
3. 对前两步重复999次（重复次数越多，得到的背景分布越”稳定“）
4. 这样我们得到有999个置换排列求得的999个Sper结果，这999个Sper结果能代表拟南芥小样本实验的抽样总体情况。
   

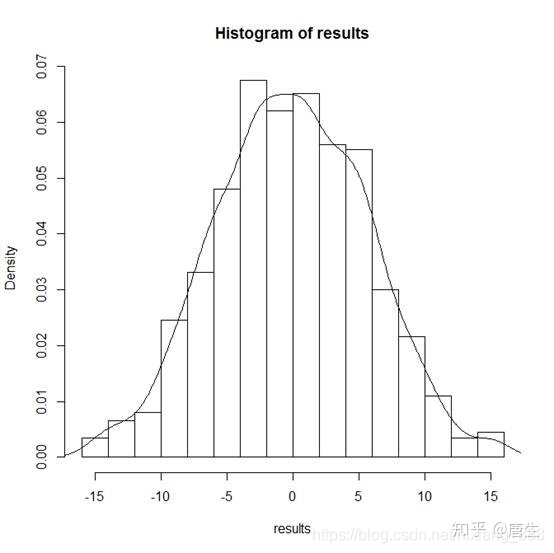
如上图所示，我们的观测值 Sobs=14 在抽样总体右尾附近，说明在零假设条件下这个数值是很少出现的。在permutation得到的抽样总体中大于14的数值有9个，所以估计的P-value是9/999=0.01

最后还可以进一步精确P-value结果（做一个抽样总体校正），在抽样总体中加入一个远大于观测值 Sobs=14的样本，最终的P-value=(9+1)/(999+1)=0.01。（为什么这样做是一个校正呢？自己思考:)）结果表明我们的原假设不成立，加入生长素起到了促使拟南芥的根系发育的作用。

3. 在线性回归中的应用

置换检验是一种非常重要的统计思想，并不只应用于两样本或多样本比较问题当中。实际上，它和Bootstrap方法类似，也是通过重抽样得到统计量的复制，从而获得近似统计量的精确分布。和Bootstrap方法所采取的有放回抽样不同的是，置换方法可看作是不放回抽样。下面以置换检验在回归分析中的应用加以说明。

考虑一元线性回归模型

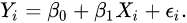
现基于置换方法对斜率 β₁ 进行检验H₀： β₁=0。相比传统方法，置换方法不需要正态性和同方差性假定。

具体操作步骤如下：

第一步， 首先通过最小二乘方法对参数 β₀, β₁ 进行估计，从而得到残差

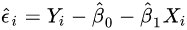
，并对β₁构造F型统计量

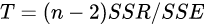
第二步， 对残差

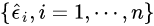
进行随机置换得到置换的误差 e^*。 令

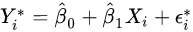
第三步，基于 （ X_i， Y_i^*） 重新拟合回归模型，得到

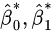
并得到统计量的置换复制 T^*；

第四步，重复步骤2-3 B次，得到相应置换后的统计量

第五步，近似p值为

4. GSEA富集分析

置换检验在GSEA的算法思路中是一个重要的组成部分：

1. 当我们将Permutation type参数设置为1000后，就相当于我们从原始所有样本中随机抽取1000个置换后的样本。
2. 接着，先计算这1000个置换样本的signal to noise scores（也可以是log2_Ratio_of_Classes等），然后再计算每个置换样本的在每个gene sets下的ES值，这个ES值就是置换检验中的统计量。
3. 最后根据这1000个ES的经验分布，计算原始样本的ES值在这分布中的位置，也就是P值，来确定是否能推翻原假设

四、t 检验和置换检验的联系与区别

1. 联系：
   • 计算了相同的 t 统计量。
2. 区别：
   • t 检验将统计量与理论分布进行比较，置换检验将统计量与经验分布比较，根据统计量值的极端性判断是否有足够的理由拒绝零假设。

五、适用场景

• 假定数据成正态分布并不合适；
• 担心离群点的影响；
• 对于标准的参数方法来说数据集太小。