机器学习—卷积神经网络

原创已于 2023-01-15 18:29:18 修改 · 425 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#cnn #深度学习

于 2023-01-15 18:27:12 首次发布

ML 专栏收录该内容

8 篇文章

订阅专栏

卷积神经网络

卷积
池化层
整体架构
经典网络架构
感受野

卷积中输入的是三维数据：h * w * c （channel）
整体架构：输入层、卷积层、池化层、全连接层

卷积

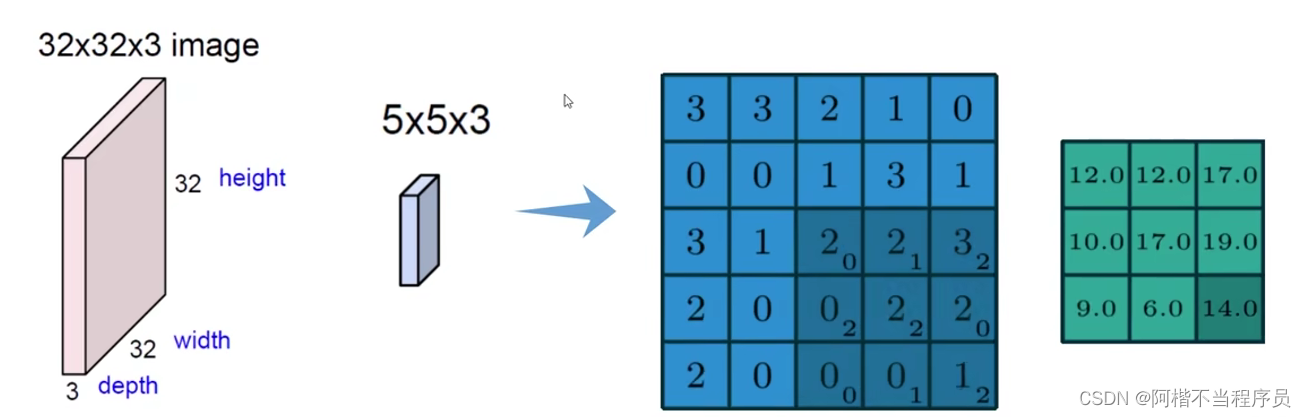
如图像数据维度为三维，32 * 32 * 3，取其中一小块区域进行特征提取；

然后根据该区域的值与权重进行内积，得到特征值。

绿色矩阵就是执行一次卷积后得到的结果——特征图，

颜色通道

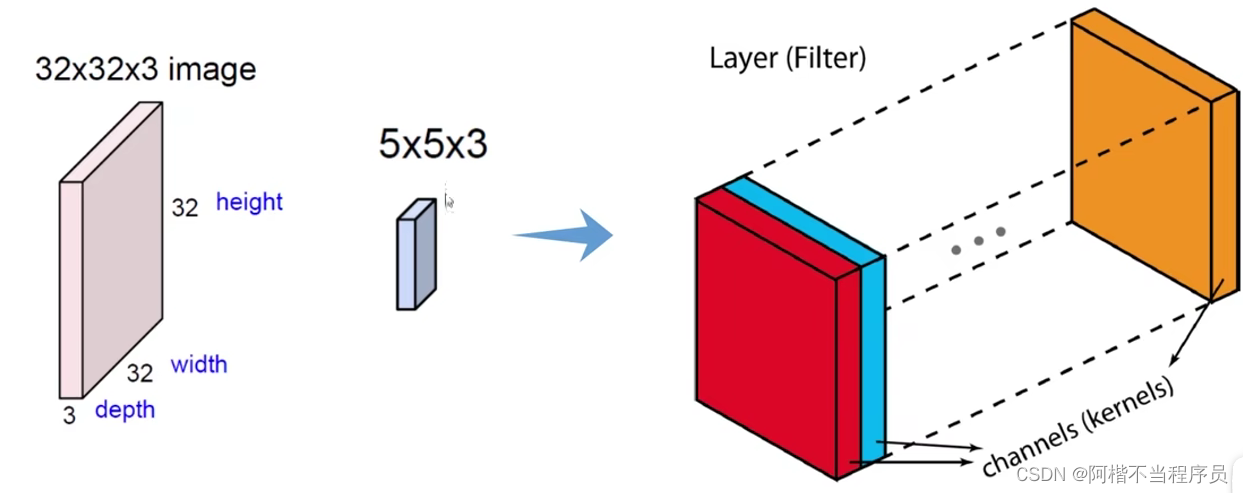
对于每一个颜色通道，都会进行计算，最终相加。

特征值

每一个区域对应三种颜色通道，将每一个通道的权重参数与该区域进行内积后，得到特征值；

最后将三种颜色通道的特征值相加，在加偏置项，即为该区域值。

特征图个数

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-v2nJYmOj-1673777965528)(../typora_image/image-20221219201936304.png)]

可以取多种filter方法进行特征提取；

如图，一个特征图的维度是28*28，经过6次filter后，得到维度为28 * 28 * 6 的特征图；

堆叠的卷积层

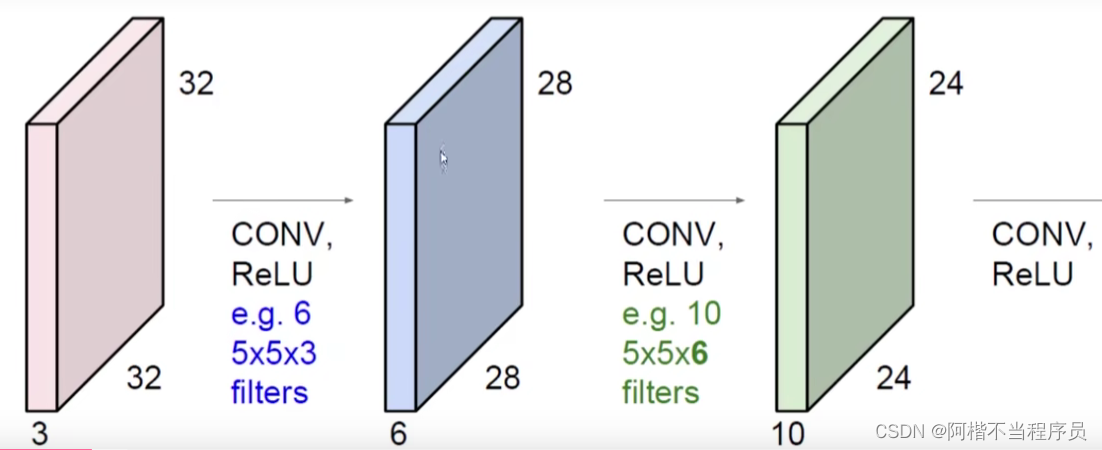
一次卷积是不够的，需要多次重复的卷积，而后一次卷积都是在前一次的基础上来进行的；

卷积层参数
- 滑动窗口步长
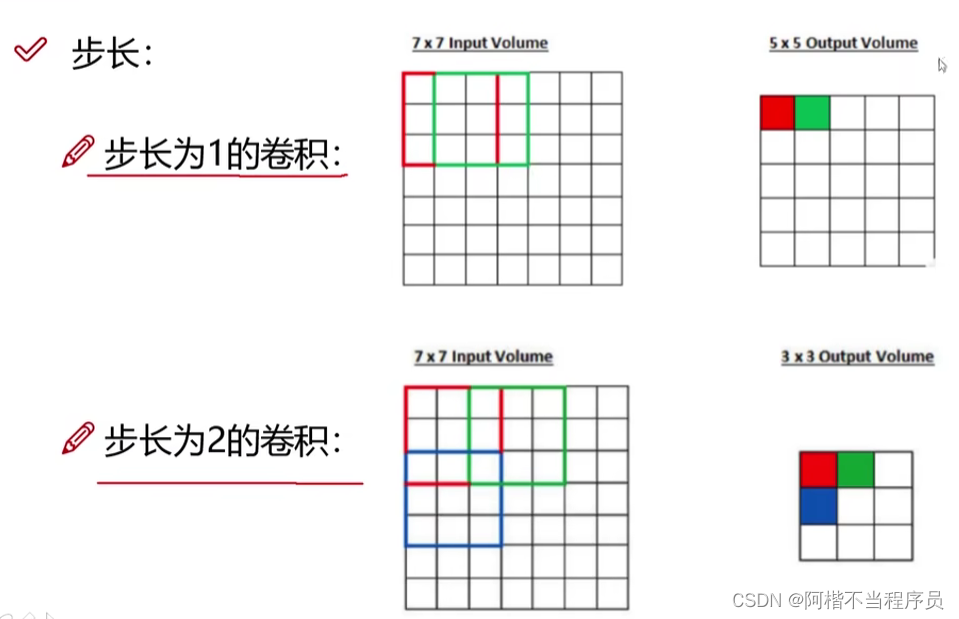
指定移动的步长越小（更细，更丰富），获取的特征值就越多，得到的特征图维度就越大。
- 卷积核尺寸：一次选取的值的维度（方框大小）。
步长与尺寸要保证神经元整齐对称地滑过输入数据体。
- 边缘填充：对原始矩阵扩充的维度，使边界点有更多计算的次数。填充的值都为0。
- 卷积核个数：需要的特征图个数。
卷积计算公式

$长度：H_2=\frac{H_1-F_H+2P}{S}+1 \\[2ex] 宽度：W_2 = \frac{W_1-F_W+2P}{S}+1$

W1、H1：表示输入的宽度、长度；

W2、H2：表示输出的特征图宽度、长度；

FH、FW：卷积核长、宽；

S：滑动窗口步长；

P：边界填充维度（加几圈0）；

卷积参数共享

一个区域中进行遍历计算，都用相同的卷积核进行计算。

如数据为32 * 32 * 3的图像，用10个5 * 5 * 3的filter进行卷积操作，所需的权重参数个数：

$5 * 5 * 3 = 75$ ，即每一个卷积核有75个参数，10个卷积核则有750个参数，加上偏置项b，则有 $750 + 10 = 760$ 个权重参数。

池化层

作用：压缩、下采样。

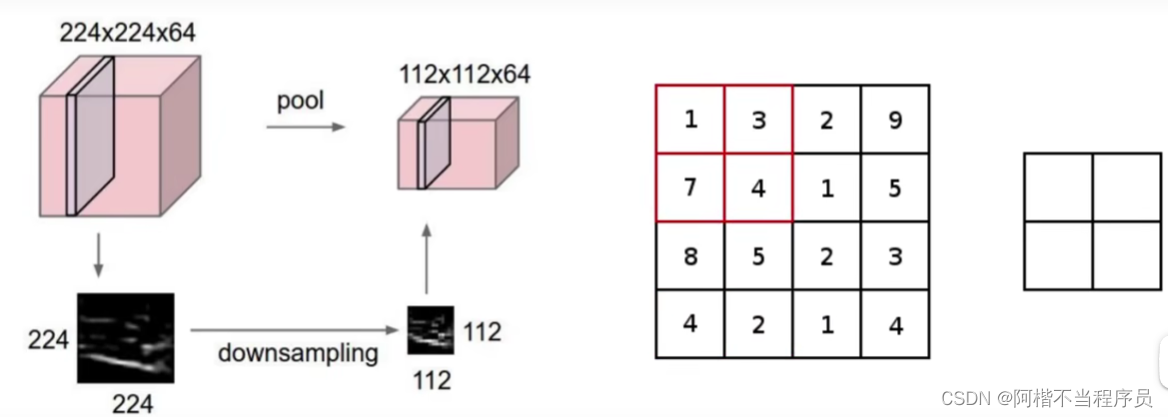
将数据维度压缩成原来1/4的大小；

指定一种方法，去选取较为重要的特征。

最大池化（MAX POOLING）

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-mu6i2oyY-1673777965530)(../typora_image/image-20221219220120993.png)]

如图，该方法从四个区域里面摘取出最大的值，成为新的矩阵。

整体架构

CONV——RELU——CONV——RELU——POOL——……——全连接层
激活层、池化层没有参数计算，不计入总层数。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-FO26uA7e-1673777965530)(../typora_image/image-20221220221007702.png)]

经典网络架构

Alexnet

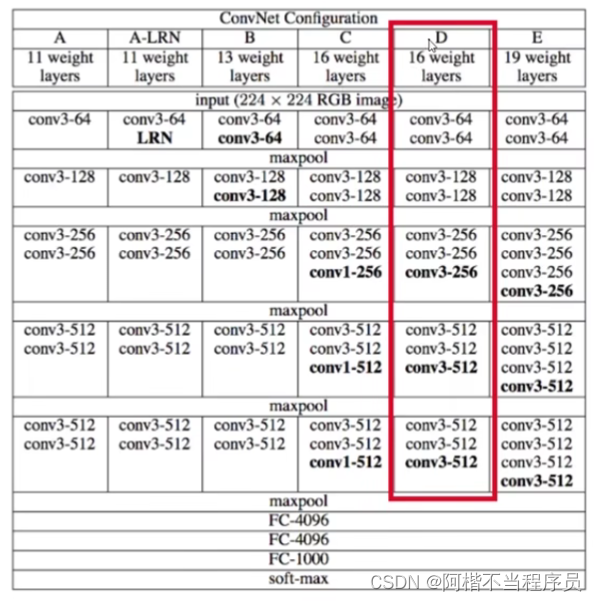
在这里插入图片描述

特点：卷积大小都是3 * 3；pooling后会损失信息，在下一层会使数据翻倍；

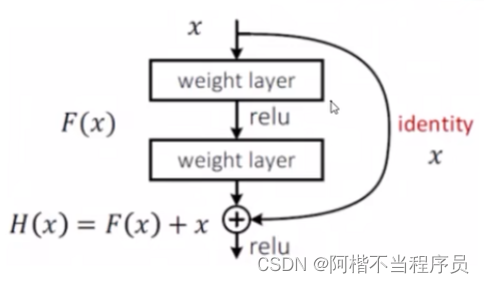
Resnet（残差神经网络）

深度网络遇到的问题：层数少比层数多的模型误差更小，是否需要去除某些层？

解决方案：

当加入某一层会使模型效果降低时，使其权重为零，来让该层不影响原模型。

如图，经过两层处理后的值+未经过处理的值（x），如果Loss上升，则将该两层权重参数设为0，这能保证模型逐步加入layer不回比原来的差。

感受野

后一层能感受到前一层的输入维度大小

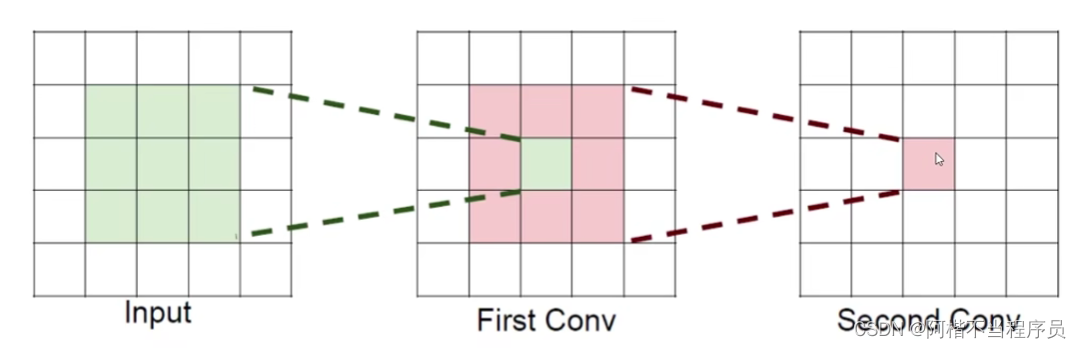
假设输入维度为h * w * c ，并且都是用c个卷积核（得到c个特征图）：

一个7 * 7卷积核所需参数： $C*(7*7*C)=49C^2$

3个3 * 3卷积核所需参数： $3*C*(3*3*C)=27C^2$
说明堆叠小的卷积核所需的参数更少一些，并且卷积过程越多，特征提取就会越细致，加入的非线性变换也随之增多，还不会增权重参数。