LeetCode 51 N-Queens

The n-queens puzzle is the problem of placing n queens on an n×n chessboard such that no two queens attack each other.

Given an integer n, return all distinct solutions to the n-queens puzzle.

Each solution contains a distinct board configuration of the n-queens' placement, where 'Q' and '.' both indicate a queen and an empty space respectively.

For example,
There exist two distinct solutions to the 4-queens puzzle:

[
 [".Q..",  // Solution 1
  "...Q",
  "Q...",
  "..Q."],

 ["..Q.",  // Solution 2
  "Q...",
  "...Q",
  ".Q.."]
]

八皇后问题，是一个古老而著名的问题，是回溯算法的典型案例。该问题是国际西洋棋棋手马克斯·贝瑟尔于1848年提出：在8×8格的国际象棋上摆放八个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上.

以下摘自matrix67位运算简介及实用技巧（三）：进阶篇(2)

  
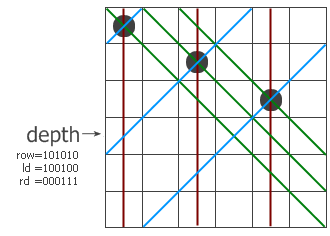
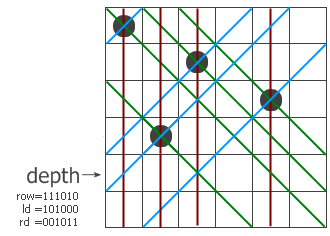
   过程带三个参数，col、left和right，分别表示在纵列和左右两个对角线方向的限制条件下这一行的哪些地方不能放。我们以6×6的棋盘为例，看看程序是怎么工作的。假设现在已经递归到第四层，前三层放的子已经标在左图上了。红色、蓝色和绿色的线分别表示三个方向上有冲突的位置，位于该行上的冲突位置就用col、left和right中的1来表示。把它们三个并起来，得到该行所有的禁位，取反后就得到所有可以放的位置（用status来表示）。pos表示取出status最右边的那个1。这样，pos就表示该行的某个可以放子的位置，把它从status中移除并递归调用dfs过程。注意递归调用时三个参数的变化，每个参数都加上了一个禁位，但两个对角线方向的禁位对下一行的影响需要平移一位。最后，如果递归到某个时候发现col=111111了，说明六个皇后全放进去了，此时程序找到一个解。

Runtime:  6 ms  beats 77.98% of java submissions

	private long MASK;
	private int queens;//皇后的个数

	public List<List<String>> solveNQueens(int n) {
		queens = n;
		List<List<String>> res = new ArrayList<>();
		MASK = (1 << n) - 1;
		dfs(0L, 0L, 0L, new ArrayList<>(), res);
		return res;
	}

	private void dfs(long col, long left, long right, List<String> crt, List<List<String>> res) {
		if (col == MASK) {//col==MASK的时候证明n个皇后都放进去了
			res.add(new ArrayList<>(crt));
			return;
		}
		long status = ~(col | left | right) & MASK;//三个并起来,得到该行所有的禁位,取反后就得到所有可以放的位置
		while (status > 0) {
			long pos = status & -status;//取出status最右的1位
			crt.add(getString(pos));
			int index = crt.size();
			dfs(col | pos, (left | pos) << 1, (right | pos) >> 1, crt, res);
			crt.remove(index - 1);
			status -= pos;
		}
	}

	/**
	 * pos = 001000二进制相当于"..Q..."
	 */
	private String getString(long pos) {
		char[] vals = new char[queens];
		Arrays.fill(vals, '.');
		int i = queens;
		while (pos > 0) {
			pos >>= 1;
			i--;
		}
		vals[i] = 'Q';
		return new String(vals);
	}