《Think Python》练习 4-1：本章示例代码栈图、停止点偏离思考

第4章 案例研究：接口设计

练习 4-1 本章示例代码栈图、停止点偏离思考

【习题 4.1.1】 画一个栈图来显示函数 circle(bob, radius) 运行时的程序状态。
《Think Python》第4章示例代码（仅circle相关，完整版点击）：

"""This module contains a code example related to

Think Python, 2nd Edition
by Allen Downey
http://thinkpython2.com

Copyright 2015 Allen Downey

License: http://creativecommons.org/licenses/by/4.0/
"""

from __future__ import print_function, division

import math
import turtle


def polyline(t, n, length, angle):
    """Draws n line segments.

    t: Turtle object
    n: number of line segments
    length: length of each segment
    angle: degrees between segments
    """
    for i in range(n):
        t.fd(length)
        t.lt(angle)


def arc(t, r, angle):
    """Draws an arc with the given radius and angle.

    t: Turtle
    r: radius
    angle: angle subtended by the arc, in degrees
    """
    arc_length = 2 * math.pi * r * abs(angle) / 360
    n = int(arc_length / 4) + 3
    step_length = arc_length / n
    step_angle = float(angle) / n

    # making a slight left turn before starting reduces
    # the error caused by the linear approximation of the arc
    t.lt(step_angle/2)
    polyline(t, n, step_length, step_angle)
    t.rt(step_angle/2)


def circle(t, r):
    """Draws a circle with the given radius.

    t: Turtle
    r: radius
    """
    arc(t, r, 360)


# the following condition checks whether we are
# running as a script, in which case run the test code,
# or being imported, in which case don't.

if __name__ == '__main__':
    bob = turtle.Turtle()

    # draw a circle centered on the origin
    radius = 100
    bob.pu()
    bob.fd(radius)
    bob.lt(90)
    bob.pd()
    circle(bob, radius)

    # wait for the user to close the window
    turtle.mainloop()

【求解】 在加入 print 语句之后，发现 bob 的值是 <turtle.Turtle object at 0x10eb04a90>，而不是 turtle.Turtle()

所属函数	变量
__ main__	bob ——> <turtle.Turtle object at 0x10eb04a90>
__ main__	radios ——> 100
circle	t ——> <turtle.Turtle object at 0x10eb04a90>
circle	r ——> 100
arc	t ——> <turtle.Turtle object at 0x10eb04a90>
arc	r ——> 100
arc	angle ——> 360
polyline	t ——> <turtle.Turtle object at 0x103ba5518>
polyline	n ——> 160
polyline	length ——> 3.9269908169872414
polyline	angle ——> 2.25
因为 优快云 的 Markdown 文字两侧连打2个下划线是加粗，所以main的前面多了个空格（强迫症勿怪）

【习题 4.1.2】 在 4.7 节中的 arc 函数并不准确，因为使用多边形模拟近似圆，总是会在真实的圆之外。因此，Turtle 画完线之后会停在偏离正确的目标几个像素的地方。我的解决方案里展示了一种方法可以减少这种错误的效果。阅读代码并考虑是否合理。如果你自己画图，可能会发现它是如何生效的。
【求解】 先对比代码有何不同
《4.7 节》的 arc 函数：

def arc(t, r, angle):
	arc_length = 2 * math.pi * r * angle / 360
	n = int(arc_length / 3) + 1
	step_length = arc_length / n
	step_angle = angle / n

	for i in range(n):
		t.fd(step_length)
		t.lt(step_angle)

《练习 4-1》的arc 函数：

def polyline(t, n, length, angle):
    """Draws n line segments.

    t: Turtle object
    n: number of line segments
    length: length of each segment
    angle: degrees between segments
    """
    for i in range(n):
        t.fd(length)
        t.lt(angle)


def arc(t, r, angle):
    """Draws an arc with the given radius and angle.

    t: Turtle
    r: radius
    angle: angle subtended by the arc, in degrees
    """
    arc_length = 2 * math.pi * r * abs(angle) / 360
    n = int(arc_length / 4) + 3
    step_length = arc_length / n
    step_angle = float(angle) / n

    # making a slight left turn before starting reduces
    # the error caused by the linear approximation of the arc
    t.lt(step_angle/2)
    polyline(t, n, step_length, step_angle)
    t.rt(step_angle/2)

《练习 4-1》示例代码给出的解决方案是“在画圆前轻微左偏”，理由是“错误是由弧的线性相似导致的”。

关于 弧的线性相似误差 ：
《Think Python》又名《重拾三角函数》。
由于本人脱离学校太久，总之根据本人已经没法证明的三角函数求极限理论，当近似圆中每个小三角夹角足够小的时候，近似圆就越接近圆，真实的圆并不完全在近似圆之内或之外，真实圆的弧不停的跨过近似圆的边，像这样：

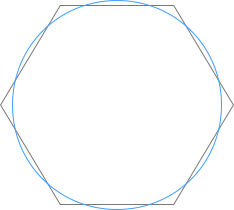
这种近似圆与真实圆的误差会导致多边形的角在真实圆之外，即每当开始或停止画直线的时候，乌龟会停在多边形的角上，即真实圆之外。

关于处理方案：

#左转半个step_angle
t.lt(step_angle/2)

#画一个近似圆
for i in range(n):
	t.fd(length)
    t.lt(angle)
    
#右转半个step_angle
t.rt(step_angle/2)

我将 arc 函数引用的 polyline 函数中的 for 循环展开了，可以先看出来处理方案的 arc 函数是先左转半个 step_angle 的角度，再画一个 完整的 近似圆，画完后再讲乌龟右转半个 step_angle 归位：

老实说我并不觉得这种 “再画圈前稍微左转一点点（making a slight left turn before starting reduces）”的骚操作除了让画出的近似圆比之前的右偏半个 step_angle 对于画出的多边形本身并没有任何影响，为何作者会认为这种操作减小了误差呢？虽然作者说了“如果你自己画图，可能会发现它是如何生效的”，但是我画了更理解不了……
我打算写完第四章作业后，发个帖子找人问问，如果有大佬指点的话，会更新在这里。
我回来了……
在做【练习 4-4：字母表】时发现，如果删除掉

#左转半个step_angle
t.lt(step_angle/2)
    
#右转半个step_angle
t.rt(step_angle/2)

仅保留

#画一个近似圆
for i in range(n):
	t.fd(length)
    t.lt(angle)

当你在画J的时候，如果先画一竖，再左移直径画一个半圆，你会发现，根本接不上……
代码：

#引入数学模块、乌龟模块
import math
import turtle

#调用乌龟画图、提高画弧速度
bob = turtle.Turtle()
bob.delya = 0.01

#多边线
def polyline(t, n, length, angle):
    for i in range(n):
        t.fd(length)
        t.lt(angle)

#弧
def arc(t, r, angle):
    arc_length = 2 * math.pi * r * abs(angle) / 360
    n = int(arc_length / 4) + 3
    step_length = arc_length / n
    step_angle = float(angle) / n
    #t.lt(step_angle/2)
    polyline(t, n, step_length, step_angle)
    #t.rt(step_angle/2)

#线段
def line(t, l):
    t.fd(l)
        
#test:J
def draw_j(t, l):
    t.rt(90)
    line(t, l)
    t.pu()
    t.rt(90)
    line(t, l/2)
    t.lt(90)
    t.pd()
    arc(t, l/4, 180)
    
draw_j(bob,200)
turtle.mainloop()

效果：

说明 t.lt(step_angle/2) 转的微小角度才是正确的，不转所画的弧线虽然尺寸没问题，但是位置以起点为中心左偏了 t.lt(step_angle/2) 角度。
加上这两行代码（解除注释）后：

#弧
def arc(t, r, angle):
    arc_length = 2 * math.pi * r * abs(angle) / 360
    n = int(arc_length / 4) + 3
    step_length = arc_length / n
    step_angle = float(angle) / n
    t.lt(step_angle/2)
    polyline(t, n, step_length, step_angle)
    t.rt(step_angle/2)

效果：

仔细想了下函数 arc(t, r, angle) 的画法，如果开头不左转 t.lt(step_angle/2) 的话，相直线向下画第1笔，再开始“转一个小角度 - 再画一笔”的循环：

这就造成了一个问题：终点没有跟起点水平（没有 t.lt(step_angle/2) 的终点是红色，有 t.lt(step_angle/2) 的终点是绿色），造成了这种效果：

仔细想了一下，数学原因是：由于我们是用很短的直线模拟的曲线，起点和终点的切线斜度就是第一根线和最后一根线的斜度，第一根直线的斜度是0、最后一根切线的斜度是 cot(step_angle)，没办法像真正的弧线一样做到起点和终点的切线斜度相同，故需要匀一下，让起点多 step_angle/2，终点少 step_angle/2。