如何找寻数据对应关系

        为了找出设置值和AD值之间的数学关系，我们可以对这些数据进行线性回归分析。但是由于没有直接的物理背景或转换公式的说明，我们暂时假设两者之间存在线性关系，并尝试拟合一条直线来描述这种关系。

线性回归的目标是找到斜率（m）和截距（b），使得下述方程成立：

设置值 = m × AD值 + b

1 下载安装python

        略。

2 安装数据分析相关库

        在Python环境中，我们需要用到numpy和pandas进行数据处理，并使用scikit-learn进行线性回归分析。您可以使用pip（Python包管理器）来安装这些库：

打开命令行（对于Windows用户是CMD或PowerShell；对于Mac/Linux用户是终端），然后分别输入以下命令来安装这些库：

pip install numpy pandas scikit-learn

pip install matplotlib

3 代码 

import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression


# 假设你的数据如下
setting_values = [5, 10, 25, 35, 50, 65, 85, 95, 125, 150]
ad_values = [155, 318, 808, 1134, 1623, 2111, 2764, 3090, 4067, 4834]

# 创建DataFrame以适应模型输入格式
df = pd.DataFrame({'Setting': setting_values, 'AD': ad_values})

# 训练模型
model = LinearRegression()
model.fit(df[['AD']], df['Setting'])

# 获取斜率和截距
slope = model.coef_[0]
intercept = model.intercept_

# 预测函数
def predict_setting(ad_value):
    return slope * ad_value + intercept

# 输出模型的斜率（系数）和截距
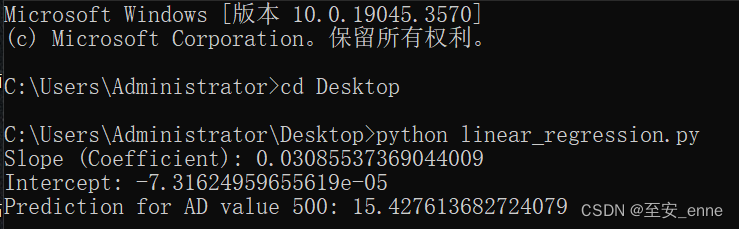
print(f"Slope (Coefficient): {model.coef_[0]}")
print(f"Intercept: {model.intercept_}")

# 假设做了一个预测
# 假设我们想预测AD值为500时对应的设置值
some_ad_value = 500
example_prediction = predict_setting(some_ad_value)
print(f"Prediction for AD value {some_ad_value}: {example_prediction}")
plt.scatter(df['Setting'], df['AD'])
plt.plot(df['Setting'], model.predict(df[['AD']]), color='red')
plt.xlabel('Setting')
plt.ylabel('AD')
plt.title('Linear Regression Fit')
plt.show()
# （若要绘制图表，请继续添加相关matplotlib绘图代码）

 

这段代码用于执行线性回归分析，并基于给定的setting_values和ad_values数据集预测目标变量（设置值）：

1. 首先，导入所需的库：

   • pandas 用于处理数据，创建DataFrame结构。
   • matplotlib.pyplot 用于数据可视化，绘制散点图和拟合直线。
   • sklearn.linear_model.LinearRegression 用于训练线性回归模型。

2. 假设已知两个列表：setting_values 和 ad_values，它们分别代表自变量（广告投入量，AD）和因变量（某种设置值）。将这两个列表转换为一个名为df的Pandas DataFrame，其中包含两列——'Setting'和'AD'。

3. 使用LinearRegression类创建并初始化线性回归模型。

4. 使用DataFrame中的 'AD' 列作为特征向量，'Setting' 列作为目标变量来训练模型。注意这里是用AD值来预测Setting值，这与常见的使用方式相反（通常我们会用Setting值来预测AD值），但根据上下文这可能是有意为之。

5. 获取模型训练得到的斜率（系数）和截距，并打印出来。

6. 定义一个函数 predict_setting(ad_value)，它接受一个AD值作为输入，应用模型计算出对应的预测设置值。

7. 调用预测函数，使用示例AD值500进行预测，并打印预测结果。

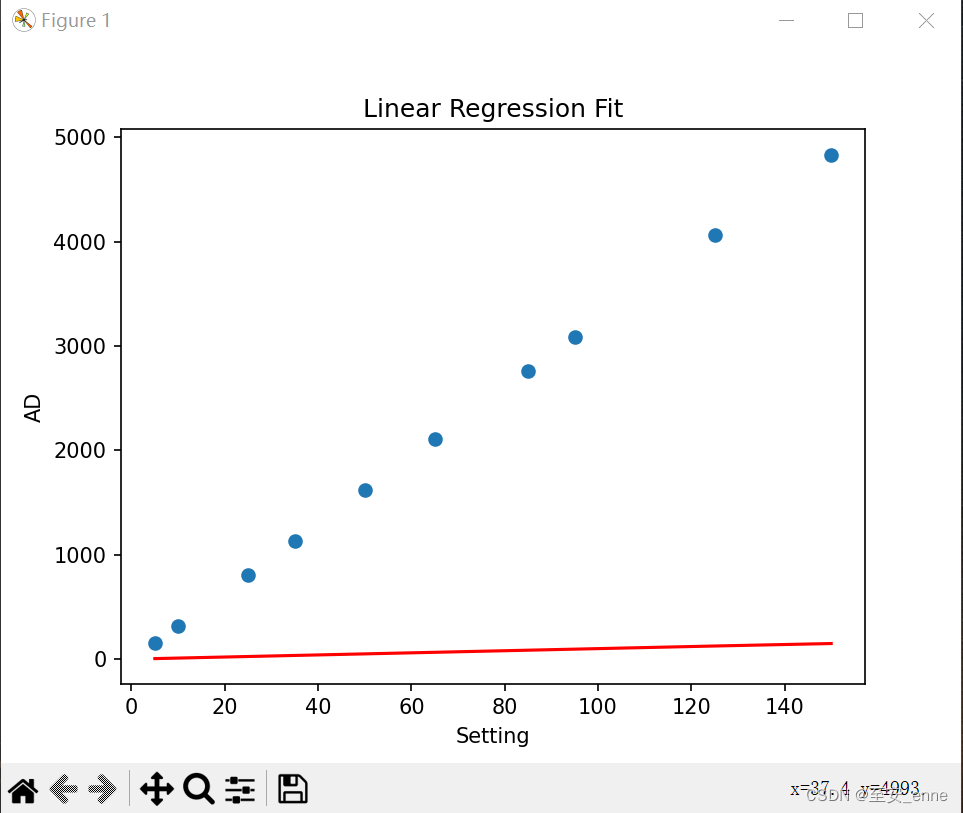
8. 使用 matplotlib 绘制原始数据的散点图，并在图上绘制由线性回归模型得到的拟合直线。此直线展示了模型对所有观测数据点趋势的估计。

9. 设置图表的标签、标题，并通过调用 plt.show() 显示最终的绘图结果。

总结：该代码实现了一个简单的线性回归分析流程，从加载数据到训练模型、预测新值以及可视化数据及其拟合情况。

4 运行及结果