无需初始化的视觉惯性导航

无需初始化的单目视觉‐惯性状态估计及其在自主微型飞行器中的应用

摘要

为了研制更小、更灵活的微型飞行器，研究界已将相机和惯性测量单元（IMU）作为状态估计与自主控制的主要传感器。本文提出了一种用于自主四旋翼飞行器的单目视觉‐惯性系统（VINS），该系统仅依赖低成本的商用相机和惯性测量单元（IMU），并描述了一种鲁棒的状态估计器，使飞行器能够在2米/秒的速度下执行轨迹飞行，滚转和俯仰角度达到20度，加速度超过4米/秒²。本文的主要创新在于提出了一种无需初始化即可估计车辆运动的方法，以及一种可实时确定尺度和度量状态信息且不会遇到任何退化问题的方法。

1 引言

微型飞行器（MAVs）由于其体积小、机动性强，是复杂受限环境中执行任务的理想平台。近年来，在复杂无全球定位系统（GPS）环境下部署搭载传感器的自主微型飞行器（MAVs）取得了显著成功。特别是由相机和低成本惯性测量单元（IMU）组成的单目视觉惯性导航系统（VINS），因其体积小、成本低，非常适合载荷受限的微型飞行器。

代价低且维护简便。然而，大多数现有的单目视觉惯性导航系统方法在缺乏良好初始状态估计的情况下无法运行，且当估计器因缺少初始条件而发生故障时，也无法在线恢复或重启[1, 2]。这类自主微型飞行器只能在已知初始条件（例如静止状态）下启动，且其工作包络受到限制，以降低估计器失效的风险。因此，本文的研究目标是开发一种可动态发射且可故障恢复的微型飞行器，使其能够自主飞行通过各种轨迹，包括悬停、直线和剧烈机动（图1）。

针对VINS的解决方案已在滤波框架[1–7]以及基于图的优化/光束法平差/平滑框架[8–10]中被提出。滤波方法由于对过去状态进行连续边缘化，具有处理速度快的优势，但由于线性化点过早固定，其性能可能次优。基于图的方法得益于对状态的迭代重线性化，但需要更多的计算资源。通过适当边缘化，可以获得具有恒定复杂度的滑动窗口基于图的框架[8]。文献[11]中比较了滤波与基于图的方法，作者报告称两类方法的结果几乎相同。然而，验证所用平台仅配备了一个光学流传感器，无法实现长期的特征跟踪，这限制了基于图方法的性能，因为始终无法构建足够连通的图。

我们还可以将视觉惯性导航系统（VINS）解决方案分为松耦合[1]或紧耦合[2–7, 9, 10]。松耦合方法通常使用独立的视觉处理模块（例如PTAM[12]）进行尺度不确定的位姿估计，并通过滤波器将视觉位姿与惯性测量单元（IMU）融合以实现尺度估计。紧耦合方法通常能获得更好的估计结果（最多存在线性化误差），因为它们以系统化的方式整合了相机测量和噪声模型。

然而，由于非线性视觉惯性导航系统底层的线性化求解器，上述所有方法都需要良好的初始化。

关于无需初始化的视觉惯性导航系统不进行初始化的开创性工作在[13]中被提出，作者建议在滑动窗口中首个位姿的机体坐标系下执行估计。提出了一种IMU预积分技术来处理多速率传感器测量。作者表明，系统的非线性主要仅来源于旋转漂移。

最近的研究表明，通过假设姿态已知或通过短期积分陀螺仪输出来估计旋转，视觉惯性导航系统（VINS）可以在一个线性的闭式解[14–18]中求解。研究表明，初始重力矢量和机体坐标系速度都可以线性估计。这些结果具有重要意义：良好的VINS问题初始化实际上可能并非必需。然而，[14]仅限于使用固定数量的少量IMU测量值，这使其对IMU噪声非常敏感。在滑动窗口中利用多个IMU测量值的方法[15–18]在处理大量IMU测量值时扩展性较差，因为它们依赖于长时间内的加速度计输出双重积分。此外，这些闭式方法未考虑系统的噪声特性，从而导致次优结果。

单目视觉惯性导航系统的另一个问题是由于退化运动导致的尺度模糊。众所周知，为了使尺度可观测，至少需要两个轴上的加速度[2, 4, 16]。然而，对于微型飞行器而言，诸如悬停或匀速运动等退化运动是不可避免的。文献[7]通过提出一种后进先出（LIFO）滑动窗口方法首次解决了悬停情况。然而，由于仅对状态进行测量更新的机制，[7]产生了悲观的协方差估计。

为了解决初始化、故障恢复和退化运动的问题，本文的贡献可归纳为三方面。

• 我们提出了一种用于单目视觉惯性导航系统的线性滑动窗口公式，能够在无需任何先验初始信息的情况下估计必要的导航状态（速度与姿态）（第2和第4节）。
• 我们通过提出一种双向边缘化方案（第3节）来解决退化运动和尺度不可观测性问题。
• 我们通过实验表明，所提出的方法能够在无需初始化的情况下实现度量状态估计。我们还表明，我们的系统能够处理退化运动情况（第6节）。

2 线性滑动窗口视觉惯性导航系统估计器

2.1 符号说明

我们将(G)视为地球惯性坐标系，(B)视为当前IMU机体坐标系，(Bk)视为第k次成像时的相机坐标系。注意，惯性测量单元通常以比相机更高的频率运行，且在两次相机图像之间可能存在多个惯性测量单元测量值Bk和Bk+1。我们假设相机和惯性测量单元已预先校准，使得相机光轴与惯性测量单元的z轴对齐。pXY、vXY和RYX分别是坐标系X相对于坐标系Y的三维位置、速度和旋转。gG=[0, 0, g]T是世界坐标系中的重力矢量，而gX是表示在坐标系X中的地球重力矢量。

2.2 问题描述

给定两个时间点（对应于两个图像帧），在世界坐标系中表示的位置和速度的IMU传播模型可以写为：

$$
p_{B}^{G_{k+1}} = p_{B}^{G_k} + v_{B}^{G_k} \Delta t + \int\int_{B_k}^{B_{k+1}} (R_{G}^{B} a_B - g_G) dt^2
$$
$$
v_{B}^{G_{k+1}} = v_{B}^{G_k} + \int_{B_k}^{B_{k+1}} (R_{G}^{B} a_B - g_G) dt
$$

其中 $a_B$ 是机体坐标系中的加速度计测量值，$\Delta t$ 是 $B_k$ 和 $B_{k+1}$ 之间的时间差。可以看出，在使用惯性测量单元测量值进行状态传播时，需要知道世界坐标系与机体坐标系之间的旋转关系。而这种旋转关系只有在已知车辆初始姿态的情况下才能确定，但在车辆动态发射或从估计器故障中恢复时，初始姿态通常是未知的。

然而，如文献[13]所建议，若将IMU传播模型的参考坐标系固定在VINS系统的初始位姿上（即我们试图估计的第一个位姿），则公式(1)可重写为：

$$
p_{B_0}^{B_{k+1}} = p_{B_0}^{B_k} + v_{B_0}^{B_k} \Delta t - g_{B_0}\Delta t^2/2 + R_{B_0}^{B_k} \alpha_{B_k}^{B_{k+1}}
$$
$$
v_{B_0}^{B_{k+1}} = v_{B_0}^{B_k} - g_{B_0}\Delta t + R_{B_0}^{B_k} \beta_{B_k}^{B_{k+1}}
$$
$$
\alpha_{B_k}^{B_{k+1}} = \int\int_{B_k}^{B_{k+1}} R_{B_k}^{B} a_B dt^2
$$
$$
\beta_{B_k}^{B_{k+1}} = \int_{B_k}^{B_{k+1}} R_{B_k}^{B} a_B dt
$$

其中 $R_{B_0}^{B_k}$ 是自 $B_0$ 以来的旋转变化，可通过结合积分陀螺仪测量值和相对极线约束获得（见第2.3节）。$\alpha_{B_k}^{B_{k+1}}$ 和 $\beta_{B_k}^{B_{k+1}}$ 可仅通过 $\Delta t$ 内的IMU测量值得到。可以看出，所有关键量（$p_{B_0}^{B_k}$、$v_{B_0}^{B_k}$、$g_{B_0}$）的更新方程现在均为线性。因此，即使在没有任何初始条件知识的情况下，VINS系统也可能以线性方式求解。

2.3 线性旋转估计

式(2)中的IMU传播模型只有在提供良好的旋转估计时才是线性的。尽管对陀螺仪测量值进行积分可以得到合理的旋转估计，但它仍会随时间产生漂移。因此，我们利用额外的对极约束来消除旋转漂移。我们希望在满足以下条件的情况下估计 $R_{B_0}^{B_k}$，k= 0,…,N：

$$
R_{B_0}^{B_0} = I_3, \quad R_{B_0}^{B_j} = \hat{R} {B_i}^{B_j} R {B_0}^{B_i}
$$

其中 $\hat{R}_{B_i}^{B_j}$ 是通过积分两个连续图像之间的陀螺仪测量，或通过寻找当前图像与对应历史图像之间的本质矩阵来获得的旋转。对于每张输入图像，我们尝试计算该图像与滑动窗口内所有其他图像之间的本质矩阵。

与[19]上述系统类似，可以通过放松旋转的正交约束来线性求解。具体而言，对于一对旋转矩阵 $R_{B_0}^{B_i}$、$R_{B_0}^{B_j}$ 及其相对约束 $\hat{R}_{B_i}^{B_j}$，我们有：

$$
[I_3, -\hat{R}_{B_i}^{B_j}]\begin{bmatrix} r_k^i \ r_k^j \end{bmatrix} = 0 \quad k= 1, 2, 3
$$

其中 $r_k^i$ 是 $R_{B_0}^{B_i}$ 的第 $k$ 列。松弛近似旋转矩阵的解可通过系统（4）的右奇异矩阵的最后三列求得。真实旋转矩阵随后可通过在近似旋转矩阵上施加单位奇异值得到：$R_{B_0}^{B_i} = UV^T$，其中 $\bar{R}_{B_0}^{B_i} = USV^T$ 是一个近似旋转矩阵。此后，我们假设滑动窗口内的旋转分量已知且无噪声。

2.4 线性滑动窗口估计器

我们采用一种紧耦合的、基于滑动窗口图的[8]方法，因其具有恒定计算复杂度，并能融合多观测的约束以优化解。完整状态向量可表示为（为简化表述，忽略转置）：

$$
X = [x_{B_0}, x_{B_0}^{B_1}, …, x_{B_0}^{B_N}, \lambda_0, \lambda_1, …, \lambda_M]
$$
$$
x_{B_0}^{B_k} = [p_{B_0}^{B_k}, v_{B_k}^{B_k}, g_{B_k}] \quad \text{for} \quad k= 1,…, N
$$
$$
p_{B_0}^{B_0} = [0, 0, 0]
$$

其中 $x_{B_0}^{B_k}$ 为第k个相机状态，N表示滑动窗口中M表示在滑动窗口内至少被观测两次的所有特征的数量。$\lambda_l$ 为第l个点特征从其首次观测起的深度。由于底层图像处理流程的特性（见第5.2节），我们可以对特征使用一维表示，这节省了大量的计算资源。我们在相机状态中保留机体坐标系速度（$v_{B_k}^{B_k}$）和重力矢量（$g_{B_k}$），这有助于减小旋转误差对估计结果的影响（见第2.5节）。

由于旋转如第2.3节所述被固定，我们可以通过收集来自惯性测量单元和单目相机的所有测量值，构建线性VINS，并通过最小化所有测量误差的马氏范数之和来求解最大似然估计：

$$
\min_X \left{ (b_p - \mu_p) + \sum_{k \in D} | z_{B_k}^{B_{k+1}} - H_{B_k}^{B_{k+1}} X |^2_{P_{B_k}^{B_{k+1}}} + \sum_{(l,j) \in C} | z_{B_j}^l - H_{B_j}^l X |^2_{P_{B_j}^l} \right}
$$

其中，测量三元组 ${\hat{z} {B_k}^{B {k+1}}, H_{B_k}^{B_{k+1}}, P_{B_k}^{B_{k+1}}}$ 和 ${\hat{z} {B_j}^l, H {B_j}^l, P_{B_j}^l}$ 分别在第2.5节和第2.6节中定义。D是所有IMU测量值的集合。C是滑动窗口内任意特征与任意相机状态之间的所有观测值的集合。${b_p, \mu_p}$ 是系统的可选先验。该系统可通过重组为以下形式求解：

$$
(\mu_p + \mu_{imu} + \mu_{cam}) X = (b_p + b_{imu} + b_{cam})
$$

其中 ${\mu_{imu}, b_{imu}}$ 和 ${\mu_{cam}, b_{cam}}$ 分别是惯性测量单元和相机测量值的信息矩阵和向量。

需要注意的是，由于代价关于状态是线性的，因此(7)中的系统在没有先验（初始条件）的情况下也可以有唯一解：

$$
(\mu_{imu} + \mu_{cam})X = (b_{imu} + b_{cam})
$$

这是实现微型飞行器动态启动和故障恢复的关键。然而，如第3节所示，单目VINS配置存在退化运动，仅使用滑动窗口内的测量值将导致尺度不可观测。在这种情况下，理想的做法是边缘化状态即将从窗口中移除的状态，并将其转换为先验以（隐式地）传播尺度。

2.5 IMU测量模型

给定局部无漂移旋转，我们可以将（2）重写为关于状态X的线性函数：

$$
\begin{bmatrix}
\alpha_{B_k}^{B_{k+1}} \
\beta_{B_k}^{B_{k+1}} \
0
\end{bmatrix}
=
\begin{bmatrix}
R_{B_k}^{B_0}(p_{B_0}^{B_{k+1}} - p_{B_0}^{B_k}) - v_{B_k}^{B_k} \Delta t + g_{B_k} \Delta t^2 / 2 \
R_{B_{k+1}}^{B_k} v_{B_{k+1}}^{B_{k+1}} - v_{B_k}^{B_k} + g_{B_k} \Delta t \
R_{B_{k+1}}^{B_k} g_{B_{k+1}} - g_{B_k}
\end{bmatrix}
= H_{B_k}^{B_{k+1}} X
$$

公式(9)中的最后一行表示对重力矢量的预测。我们为每个位姿估计重力矢量，以避免可能由累积的旋转误差带来的负面影响。除位置分量外，所有变量均独立于累积旋转 $R_{B_k}^{B_0}$，因此对旋转误差不敏感。线性IMU测量模型的形式为：

$$
z_{B_k}^{B_{k+1}} \sim N(H_{B_k}^{B_{k+1}} X, \begin{bmatrix} P_{\alpha\beta}^{B_k B_{k+1}} & 0 \ 0 & P_g^{B_k B_{k+1}} \end{bmatrix})
$$

注意，$\alpha_{B_k}^{B_{k+1}}$ 和 $\beta_{B_k}^{B_{k+1}}$ 是相关的，因为它们都来自 $\Delta t$ 时间内的IMU测量值。它们的联合协方差矩阵 $P_{\alpha\beta}^{B_k B_{k+1}}$ 可以使用文献[13]中提出的预积分技术计算。

2.6 相机测量模型

设第l个特征点首次在第i帧中被检测到。该特征点在第j个归一化图像平面 $[u_{B_j}^l, v_{B_j}^l]^T$ 上的观测可表示为：

$$
\lambda_{B_j}^l \begin{bmatrix} u_{B_j}^l \ v_{B_j}^l \ 1 \end{bmatrix} = R_{B_j}^{B_0} \left( p_{B_0}^{B_i} - p_{B_0}^{B_j} + \lambda_l R_{B_0}^{B_i} \begin{bmatrix} u_{B_i}^l \ v_{B_i}^l \ 1 \end{bmatrix} \right)
$$

其中 $\lambda_{B_j}^l$ 是特征在第j帧中的深度。我们使用跟踪而非基于描述符的方法作为数据关联的工具（第5.2节）。因此，首次观测定义了特征方向，且 $[u_{B_i}^l, v_{B_i}^l]$ 是无噪声的。注意，尽管深度初始未知，(11)相对于状态是线性的，但相对于图像测量是非线性的。未知深度转化为一个未知的测量协方差的加权因子。仍然可以将（11）重写为：

$$
0 = [-1 \quad 0 \quad u_{B_j}^l; \quad 0 \quad -1 \quad v_{B_j}^l] R_{B_j}^{B_0} \left( p_{B_0}^{B_i} - p_{B_0}^{B_j} + \lambda_l R_{B_0}^{B_i} \begin{bmatrix} u_{B_i}^l \ v_{B_i}^l \ 1 \end{bmatrix} \right) = H_{B_j}^l X
$$

相机测量模型的形式为：

$$
z_{B_j}^l \sim N(H_{B_j}^l X, \lambda_{B_j}^{2l} \bar{P}_{B_j}^l)
$$

其中 $\bar{P} {B_j}^l$ 是归一化图像平面上的特征观测噪声。注意，尽管 $\lambda {B_j}^{2l}$ 最初未知，我们可以将其初始化为场景的平均深度。在实践中，我们发现只要该初始值设置为大于实际深度，解对 $\lambda_{B_j}^{2l}$ 的初始值非常不敏感。其原因可能是未来研究的一个方向。一旦系统求解完成，我们就可以更新 $\lambda_{B_k}^{2i}$ 的值。只要 $p_{B_0}^{B_k}$ 和 $\lambda_l$ 仍处于滑动窗口内，该新值将用于后续优化。

3 处理尺度模糊

众所周知，为了使单目视觉惯性导航系统的尺度可观测，惯性测量单元必须在至少两个轴上产生非零加速度[2, 4, 16]。这对于第2节中讨论的无初始值滑动窗口估计器尤为关键2。事实上，当车辆处于退化运动状态，例如恒定速度或悬停，并且没有任何先验信息时，可以验证此时方程(8)解中的位置和速度分量可以在不违反任何约束的情况下被任意缩放。不幸的是，对于具备悬停能力的微型飞行器而言，零加速度运动是不可避免的，必须妥善处理。

如果车辆首先经历具有充分激励的加速度的一般运动（B₀,…, Bₙ），然后进入恒定速度运动（Bₙ₊₁,…, Bₙ₊ₙ），则只有当滑动窗口中包含对应于一般运动的相机状态时，尺度才可观测。然而，若可用计算资源仅允许滑动窗口中包含N个相机状态，则这种情况是不现实的。但是，如果我们能够提供 $x_{B_0}^{B_{n+1}}$ 的初始估计，就能够从Bₙ传播（而非观测）尺度到Bₙ₊₁。自然地，这可以通过在第(N+n)步将 $x_{B_0}^{B_n}$ 移出窗口时进行适当边缘化来实现。

对于悬停，如[7]所证明，如果车辆首先在（B₀,…, Bₙ₋₁）期间经历具有充分加速度激励的一般运动，然后进入悬停状态（Bₙ），则可通过使用后进先出（LIFO）滑动窗口方案保持尺度可观测性。[7]在悬停期间执行仅状态测量更新，且协方差仅在车辆退出悬停时更新一次。这是由于特征未保留在状态中，而是在执行协方差更新时被边缘化移除。然而，该方法将导致保守的协方差，因为在悬停期间获得的观测值未用于更新协方差。

3.1 双向边缘化

基于之前的讨论，我们提出了一种新颖的双向边缘化方案，用于处理恒定速度和悬停两种情况。伪代码如算法1所示。考虑完整状态向量 $X=[x_{B_0}^{B_0},…, x_{B_0}^{B_{N-1}} | \lambda_L]$，其中 $\lambda_L$ 是滑动窗口内具有至少两次观测的所有特征的集合。

当满足以下两个条件中的任意一个时，我们将下一个相机状态（$x_{B_0}^{B_N}$）添加到滑动窗口中：
1. 两幅图像之间的时间 $\Delta t$ 大于 $\delta$。
2. 在消除相对旋转后，最近两幅图像间所有公共特征的平均视差大于 $\varepsilon$。

第一个条件确保了两个相机状态之间的积分IMU测量（第2.5节）的误差是有界的，而第二个条件确保当车辆相对于场景的平移运动显著时添加新的相机状态。我们要求所有新添加的特征 $\lambda_{L+}$ 至少两次观测，以确保成功三角化（第1行）。然后，系统利用滑动窗口内所有可用的测量值以及任何可用的先验进行求解（第2行）。

我们保持一个变量 $s=\text{float/fix}$ 来指示是否应边缘化移除第二新的相机状态（$x_{B_0}^{B_{N-1}}$）或最旧的一个（$x_{B_0}^{B_0}$）。为了边缘化移除选定的相机状态 $x_{B_0}^{B_k}$，我们首先移除该相机状态以及所有首次由其观测到的特征 $\lambda_{I-}$（第5行和第13行）。然后，我们基于与被移除状态相关的所有测量值构建新的先验（第4行和第12行）：

$$
\mu_p^+ = \mu_p + \sum_{k \in D^-} H_{B_k}^{B_{k+1}^T} P_{B_k}^{-1} H_{B_k}^{B_{k+1}} + \sum_{(l,j) \in C^-} H_{B_j}^{l^T} P_{B_j}^{-1} H_{B_j}^l
$$

其中 $D^-$ 和 $C^-$ 分别为被移除的IMU和相机测量集合。边缘化可通过舒尔补[8]实现。

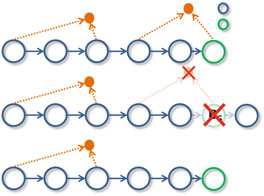
的值 $s$ 在边缘化后仅基于两个最新保留图像之间的视差重新评估（第6–9行和第14–17行）。直观上，当车辆运动较小或无运动时，我们的方法将持续移除最近的相机状态。在这种情况下保留较老的相机状态将保存恢复尺度所必需的加速度信息，同时仍保留来自被边缘化状态的所有信息。另一方面，如果车辆处于高速恒定速度运动中，则较老的相机状态将被移除并转换为后续估计的先验信息。我们注意到，在这种情况下尺度容易发生漂移。然而，在没有全局回环闭合的情况下，边缘化是向前传播尺度信息的同时保持恒定计算复杂度的最佳方法。图2展示了所提出的边缘化方法的不同工作场景。

我们还注意到，由于边缘化，(7)中的信息矩阵最终会变得稠密。然而，由于我们的公式是线性的，因此不需要迭代方法。在实践中，我们发现即使使用稠密矩阵求解器，也能在数十个相机状态和数百个特征的情况下实现实时性能。

算法1 双向边缘化

要求：
$X \leftarrow [x_{B_0},… x_{B_0}^{B_{N-1}} | \lambda_L]$
$s \leftarrow \text{float or fix}$
${\mu_p, b_p} \leftarrow \text{Prior Information}$
确保： $\Delta t > \delta$ 或 Parallax($x_{B_0}^{B_{N-1}}, x_{B_0}^{B_N}$) > $\varepsilon$

1. $X \leftarrow X \cup [x_{B_0}^{B_N} | \lambda_{L+}]$
2. 使用(6)和(7)求解X，可选地包含${\mu_p, b_p}$
3. 如果 $s = \text{浮点}$ 则
4. ${\mu_p, b_p, \lambda_{L-}} \leftarrow \text{边缘化}(x_{B_0}^{B_{N-1}})$
5. $X \leftarrow X \setminus [x_{B_0}^{B_{N-1}} | \lambda_{L-}]$
6. 如果 Parallax($x_{B_0}^{B_{N-2}}, x_{B_0}^{B_N}$) < $\varepsilon$ 则
   7. $s \leftarrow \text{浮点}$
7. 否则
   9. $s \leftarrow \text{固定}$
8. 结束判断
9. 否则
10. ${\mu_p, b_p, \lambda_{L-}} \leftarrow \text{边缘化}(x_{B_0}^{B_0})$
11. $X \leftarrow X \setminus [x_{B_0}^{B_0} | \lambda_{L-}]$
12. 如果 Parallax($x_{B_0}^{B_{N-1}}, x_{B_0}^{B_N}$) < $\varepsilon$ 则
    15. $s \leftarrow \text{浮点}$
13. 否则
    17. $s \leftarrow \text{固定}$
14. 结束判断
15. 结束判断
16. 返回 ${X, \mu_p, b_p, s}$

4 初始化与故障恢复

我们的线性VINS公式（第2节）自然支持即时初始化和故障恢复。事实上，这两项任务是相同的，因为它们都涉及在收集了足够多的图像后，求解无先验的线性系统（7）。

初始化后，为了能够同时运行用于处理尺度模糊的双向边缘化算法（第3.1节），我们维护两个子系统，分别对应两组图像/IMU测量值以及相机/特征状态。对于第一个子系统，其用于双向边缘化，当车辆处于悬停状态时，最新的两个相机状态在时间上可能相隔任意长。另一方面，第二个子系统与车辆运动无关，独立更新。它始终维持一个队列结构，当新图像到来时，最老的相机状态及其对应的测量值将被移除。通过这种方式，我们确保队列中的IMU测量值始终具有有界误差。

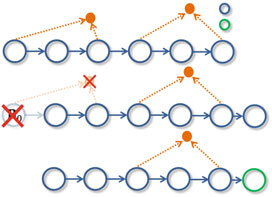
当系统处于正常运行状态时，仅求解第一个子系统，而第二个子系统仅收集数据。环境中的特征不足表示发生故障。当故障发生时，第一个数组以及所有先验信息将被丢弃。相反，我们反复尝试使用第二个子系统内的测量值来寻找有效解。一旦找到有效解，便将所有测量值重新放回第一个数组，并恢复正常运行。该故障恢复机制的框图如图3所示。

5 实现细节

5.1 实验平台

图1所示的实验平台基于Ascending Technologies, 有限责任公司的Pelican四旋翼飞行器。该平台原生配备了一个由惯性测量单元和用户可编程的ARM7微控制器组成的AutoPi‐lot板。机载主计算单元为一台英特尔NUC，搭载1.8 GHz的Core i3处理器，8 GB内存和120 GB固态硬盘。机载传感系统唯一的额外添加设备是一台配备标准镜头的mvBlueFOX‐MLC200w灰度HDR相机，以25赫兹捕获图像。752×480该平台总质量为1.39kg，推重比约为二。整个算法采用C++语言开发，并使用ROS2作为机器人操作系统中间件进行接口连接。

5.2 实时实现

尽管机载相机以25Hz的频率采集图像，但以如此高的频率执行优化（第2节）在计算上是不可行的，也是不必要的。系统在滑动窗口中以一个相机状态开始，并在该相机图像中检测到固定数量的角点特征。我们利用KLT跟踪器在高频图像序列中跟踪特征，直到将下一个相机状态添加到滑动窗口中（第3.1节）。此时，我们应用RANSAC结合对极约束进行外点剔除，然后在计算资源允许的情况下添加额外的特征。每当添加新的相机状态时，也会计算积分IMU测量（第2.5节）。所有被跟踪的特征都用于旋转估计（第2.3节），但仅有具有强角点响应的一部分特征用于位置估计（第2.4节）。如果特征总数超过阈值，我们会边缘化移除多余的特征。

我们采用多线程实现以实现实时运行。三个线程并发执行。第一个线程是前述的图像处理前端。第二个线程是主VINS优化器（第2节）和边缘化模块（第3.1节）。最后，由于计算资源的限制，我们的VINS系统以10Hz运行，处理延迟约为30毫秒。这对于微型飞行器的自主控制来说不够充分。因此，我们实现了第三个线程，利用高频IMU测量值将最新的VINS解向前传播。该线程的输出直接用作轨迹跟踪控制器的反馈。表1展示了我们系统中各组件的计算时间分解情况。结果表明，我们的算法能够稳定地在机载设备上运行。

模块	时间（毫秒）	频率（赫兹）	线程
特征跟踪	5	25	1
添加新的相机状态和特征	14	10	1
旋转估计	2	10	2
线性滑动窗口估计器	20	10	2
边缘化	17	10	2
IMU前向传播	1	100	3

6 实验结果

实验在杂乱的实验室环境中进行，使用Vicon动作捕捉系统以获取真实值进行对比。我们强调，在所有实验中，微型飞行器对环境没有任何先验知识，甚至不知道自身的初始速度和姿态。通过我们的线性公式化方法，VINS估计器在微型飞行器起飞时即完成即时初始化。这种即时初始化使得单目视觉‐惯性系统能够快速部署。

6.1 基于机载状态估计的轨迹跟踪

我们首先测试了使用VINS估计器的输出对自主微型飞行器进行反馈控制的性能。在此实验中，微型飞行器被设置为以不同的速度自主飞行八字形路径。通过最小加加速度代价函数[20]生成时间参数化的轨迹，该方法已被证明可通过降低角速度来有益于基于视觉的方法。

在图4a、c和e中，MAV以1米/秒的平均速度飞行，最大加速度为1米/秒²。众所周知，在没有全球定位系统等全局参考传感器的情况下，平台在世界坐标系中的位置和偏航角是不可观测的。事实上，我们可以看到x、y、z方向的位置漂移达到{−0.0584, 0.1191, 0.1229}米，偏航角漂移为1.563度。另一方面，MAV的机体坐标系速度以及通过估计的重力矢量推导出的姿态在整个飞行过程中仍可保持可观测。三维速度的标准差与真实值接近，如{0.0734, 0.0410, 0.0229}所示，而俯仰角和滚转角的偏差分别为{0.2487, 0.2477}，单位分别为米/秒和度。在图4b、d和f中，MAV被指令以更高的2米/秒速度飞行，并具有最大加速度为4米/秒²。位置漂移现在为{0.0319, 0.0357, 0.2329}米，而偏航漂移仍然很小，仅为0.409度。速度和姿态的误差统计分别为{0.0921, 0.0678, 0.0731}米和{0.4744, 0.4563}度。

可以看出，尽管微型飞行器在更快的轨迹下的速度、加速度以及姿态显著增加，但估计质量基本保持不变。这凸显了我们的系统在处理快速机动时的鲁棒性。

6.2 悬停性能

对于自主微型飞行器而言，使用单目视觉惯性导航系统传感器套件的一个主要问题是缺乏对度量尺度的直接测量。为此，我们通过本实验突出展示所提出的双向边缘化（第3.1节）方案的有效性。该微型飞行器从地面起飞时对其自身状态没有任何先验知识，在即时初始化完成后被指令进入悬停状态。如图5所示，由于在悬停过程中双向边缘化始终移除较新的相机状态，因此保留了具有足够视差的先前特征观测以及具有足够加速度的IMU测量值。由此实现了无漂移的六自由度完整状态估计。在悬停期间，机载位置估计与真实值吻合良好，标准差为{0.018, 0.028, 0.019}米。基于此类机载估计的悬停性能其标准差为{0.041, 0.053, 0.025}。

7 结论与未来工作

本文中，我们提出了一种据信是首个仅依赖单个现成相机和惯性测量单元（IMU）且无需精细初始化即可实现快速导航（以0.5g加速度在0.9米弧线上以2m/s速度通过）的自主四旋翼飞行器。我们克服的主要技术挑战源于状态通常不可观测这一事实，特别是对于恒定速度或悬停运动而言存在尺度模糊问题。主要的实际挑战则涉及对观测特征数量和质量的突然变化以及对机器人/相机运动依赖的鲁棒性。我们通过采用线性滑动窗口公式进行估计以及双向边缘化方案来应对这两个挑战，从而能够在没有任何先验初始信息的情况下估计必要的导航状态，同时对运动中的退化保持鲁棒性。我们在1.4公斤四旋翼飞行器上的实验结果表明，在使用动作捕捉系统的真实值测量的情况下，非结构化室内环境中的误差小于5厘米。

未来，我们希望研究控制与规划方法，以生成能够激发足够但恰好的加速度来实现尺度可观测性的运动。我们还希望开发感知与建图模块，以在杂乱环境中实现自主避障。