随机化算法

随机函数

rand

最常见的就是 rand() 函数，它生成的是伪随机数，头文件是 #include <cstdlib>。rand() 函数的缺点是比较慢。rand() 函数会返回一个 $0$ 到 RAND_MAX 的随机值，即 $0\sim 2^{31}-1$。我们可以用 srand(seed) 或 srand(time(0)) 随机种子，但是这并不必要的。需要注意的是，rand() 产生的随机数不保证均匀。

因为 rand() 太拉垮了，所以我们需要一个生成随机数质量更高的随机数生成器：mt19937，头文件是 #include<random>，范围和 rand() 相同。与它相似的随机数生成器是 mt19937_64，但是它的范围是 $0\sim 2^{63}-1$。

举个栗子：

mt19937 myrand(seed);//seed可以省略
cout<<myrand();

shuffle

shuffle 可以用于序列的随机化处理，这也是为什么它在春季测 T4 可以大展身手，头文件是 #include <algorithm>。

在使用 shuffle 时，我们需要定义随机数生成器，举个栗子：

mt19937 myrand(time(0));
shuffle(a+1,a+i+1,myrand);

爬山算法

爬山算法是一种对于 DFS 的改进，是在当前最优解附近寻找新最优解的一种方法，显然对于解的优劣分布呈单峰函数状时爬山算法是很有用的。

爬山算法常用于计算几何和毒瘤数学中。

模拟退火

模拟退火（Simulated Annealing，简称 SA）是一种随机化算法，通常用于解决方案数极多且不是单峰函数的最优解问题。

对于模拟退火，如果新状态比当前最优解更优，显然更新最优解；否则，我们以一定的随机概率接受这个更劣的新状态。

在模拟退火的过程中，我们要设定三个参数：第一个参数初始温度 $T_0$，注意这个初始温度 $T_0$ 要大一些，相当于金属加工过程中的高初温，这样才能保证模拟退火选解次数足够；第二个参数降温系数 $d$，是一个接近 $1$ 的小数，大概在 $[0.985,0.999]$ 之间；第三个参数终止温度 $T_k$，是一个接近 $0$ 的正数。

我们首先让 $T=T_0$，然后尝试转移，我们先在 $T_0$ 附近进行小小的“扰动”降温，让 $T=T\cdot d$，记录得到的新解。如果新状态比当前状态更优，显然以 $P=1$ 的概率接受这个新最优解；否则，我们记 $\Delta T=T-T^{\prime }$，选择这个新状态的概率 $P=\exp (\frac{\Delta T}{T_0})$（$\exp (x)$ 函数表示的是自然常数 $e$ 的 $x$ 次方），我们在 $(0,1)$ 之间随机选取一个数 $r$，比较它和 $P$ 的大小关系，若 $r<P$，把当前值更新为新的最优解，否则不更新。然后再进行降温操作：$T=T\cdot d$，以此类推。显然，对于当前温度 $T$，$T$ 越大接受这个新状态的概率就越大，随着迭代次数的增加，温度越来越低，接受新状态的概率也在降低，状态也趋于稳定。

如图所示，直观理解一下 qwq：

---

练手板子题

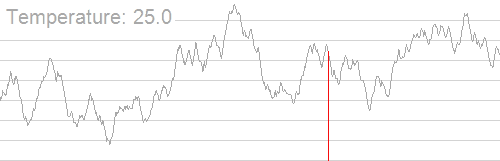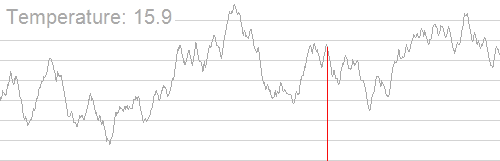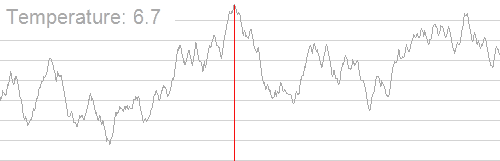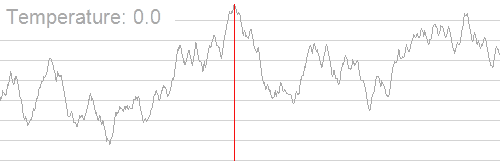
需要注意的是，这里的 (rand()*2-RAND_MAX)*t 操作是为了让它在正负 RAND_MAX 区间内选点，并且提高模拟退火正确率的方法有：让降温系数更接近 $1$、多退火几次、每次退火重置几次随机种子。

还要注意的是，在随机坐标时，我们需要在 rand() 之后乘上一个当前温度 $t$，让 rand() 的离散范围逐渐变小。

#include <bits/stdc++.h>
using namespace std;

double ansx,ansy,ans,x[1005],y[1005],n,w[1005];

double dis(double x11,double y11,double x22,double y22)
{
	double d1=x22-x11,d2=y22-y11;
	return sqrt(d1*d1+d2*d2);
}

double calc(double xx,double yy)
{
	double res=0;
	for(int i=1;i<=n;i++) res+=dis(xx,yy,x[i],y[i])*w[i];
	return res;
}

void sa()
{
	double t=5200,d=0.996;//初始温度、降温系数
	while(t>1e-15)//1e-15是最终温度
	{
		double tx=ansx+(rand()*2-RAND_MAX)*t,ty=ansy+(rand()*2-RAND_MAX)*t;
		double now=calc(tx,ty);
		double delta=ans-now;
		if(delta>0) ans=now,ansx=tx,ansy=ty;
		else if(rand()*1.0/RAND_MAX<(double)exp(delta/t)) ansx=tx,ansy=ty;
		t*=d;
	} 
}

int main()
{
	cin>>n;
	for(int i=1;i<=n;i++) cin>>x[i]>>y[i]>>w[i],ansx+=x[i],ansy+=y[i];
	ansx/=n,ansy/=n;
	ans=calc(ansx,ansy);
	int tmp=10;
	while(tmp--) 
	{
		srand(time(0));
		sa();
	}
	printf("%.3lf %.3lf",ansx,ansy);
	return 0;
}