把PDR当“里程表+指南针”,把RSSI/指纹当“路边地标”,EKF就是“交警+裁判”,在“预测”里顺着里程表滚动地图,在“更新”里用地标纠偏,靠一套可计算的误差协方差和雅可比矩阵来量化“我有多不确定”。
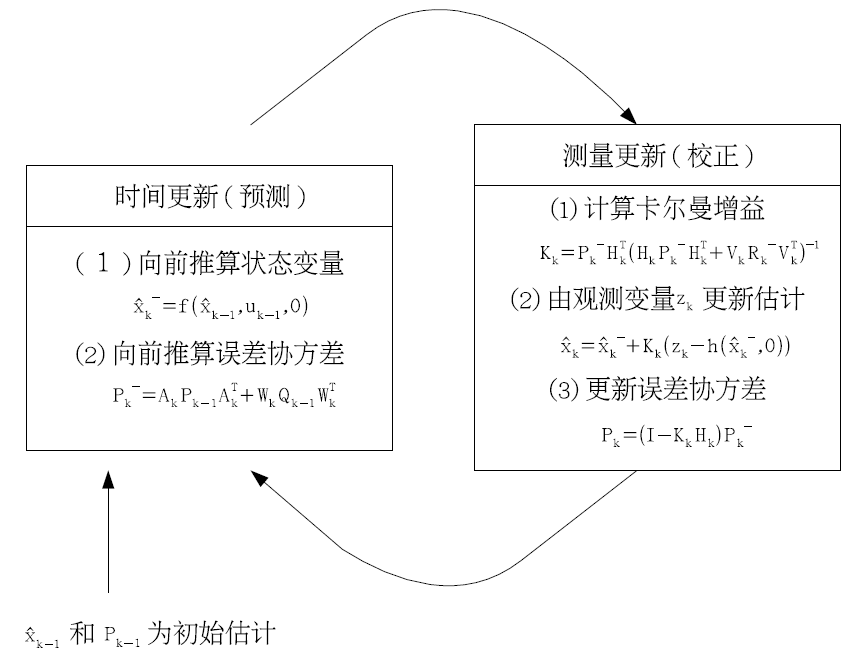
EKF 会用到的全部核心公式
把状态记为 x,协方差记为 P。离散非线性系统的标准 EKF 五步曲如下:
状态运动模型(真实世界)
![]()
- 作用: 告诉我们“如果没有新地标,仅靠里程表/IMU,我会走到哪”。
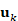 : 控制量/输入(这里常用步长 sk
: 控制量/输入(这里常用步长 sk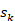 与角速率/航向)。
与角速率/航向)。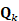 : 对“运动不完美”的不确定性度量。
: 对“运动不完美”的不确定性度量。- 观测模型(测量世界)
![]()
- 作用: 把“地标观测(如 RSSI->位置)”和“我在哪”的关系数学化。
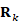 : 传感器测量噪声的不确定性。
: 传感器测量噪声的不确定性。- 预测(用运动模型滚地图)
![]()
![]()
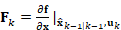 (状态雅可比)
(状态雅可比)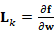 (过程噪声的注入矩阵)
(过程噪声的注入矩阵)- 更新(用地标纠偏)
-
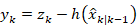
- 创新/残差)
-
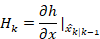
- 观测雅可比)
-
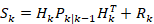
- 创新协方差)
-

- 卡尔曼增益)
-
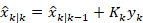
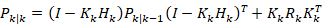
- Joseph形式,数值更稳(不容易因为数值误差把P算成非正定)。
- 观测门控(抗离群点)
-
d2=ykTSk-1yk
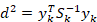
- 马氏距离) 若
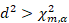 m是观测维度),判为离群,丢弃或降权。
m是观测维度),判为离群,丢弃或降权。
最常用、又够用的 2D 行人状态两种搭法:
方案 A: PDR 当“控制输入”,RSSI 当“位置观测” -
状态: ![]()
![]() : 平面位置
: 平面位置 ![]() : 航向
: 航向 ![]() : 陀螺零偏 (可选; 如果你有长期航向漂移)
: 陀螺零偏 (可选; 如果你有长期航向漂移)
输入: ![]() (步长、角速率) 观测 (RSSI/指纹):
(步长、角速率) 观测 (RSSI/指纹):![]()
方案 B: PDR 当“观测” (步移/相对位移), IMU 预测; RSSI 仍是位置观测
状态: ![]() - PDR 给出“两步之间的位移”或“步长”, 做成伪观测; IMU 负责预测。
- PDR 给出“两步之间的位移”或“步长”, 做成伪观测; IMU 负责预测。
实战建议: 方案 A 足以覆盖多数 RSSI×PDR 融合, 写法直观、实现简单。
下文以 方案 A 为主讲清公式:
步事件驱动(每次落脚更新一次)最自然:
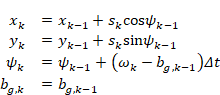
简写: ![]() 。 雅可比
。 雅可比![]() (按
(按![]() 排列):
排列):
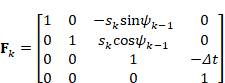
噪声注入 ![]() 与
与 ![]() (过程噪声) 直觉: 步长有误差 (脚感变化)、陀螺有噪声/漂移。令过程噪声
(过程噪声) 直觉: 步长有误差 (脚感变化)、陀螺有噪声/漂移。令过程噪声 ![]() 影响到
影响到 ![]() 。 一种常见线性化注入写法:
。 一种常见线性化注入写法:
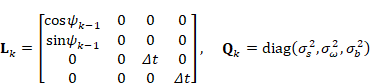
![]() : 步长噪声 (建议按步长的5%-10%起步, 如 0.05s
: 步长噪声 (建议按步长的5%-10%起步, 如 0.05s![]() )
)
![]() : 角速率噪声 (由陀螺 Allan 方差估)
: 角速率噪声 (由陀螺 Allan 方差估)
![]() : 零偏游走噪声 (慢变, 小数值)
: 零偏游走噪声 (慢变, 小数值)
含义:![]() 把步长误差投影到
把步长误差投影到 ![]() (
(![]() ), 把角噪声积成航向误差 (
), 把角噪声积成航向误差 (![]() ), 把零偏噪声积成零偏变化 (
), 把零偏噪声积成零偏变化 (![]() )。
)。
RSSI/指纹 -> 位置(二维):
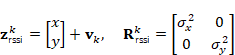
-观测函数: ![]() -
-
观测雅可比:
![]()
如何设 ![]() ?
?
指纹相似度越高 (KNN 距离小/置信度高), ![]() 越小;
越小;
信号稀疏、遮挡、异常时增大 σ![]() (甚至直接门控丢弃)。
(甚至直接门控丢弃)。
直觉: ![]() 就是你“对这次地标有多信”的数字化表达。
就是你“对这次地标有多信”的数字化表达。
这些坑,99% 的人都踩过
-
坐标系:RSSI 地图坐标与 PDR 坐标轴要一致(x 向东、y 向北;角度 0° 对齐 x 轴)。
-
时间同步:Δt 错就会“航向积分飘移”或“步移过长/过短”。
-
角度环绕:航向要做 wrap(把 ψ 压回 [−π,π))。
-
离群 RSSI:先门控再更新;多连发的异常要短期提高 R。
-
步检误触发:一步拆两步/两步合一步都会让 s 失真——步态检测要稳。
-
协方差发散:用 Joseph 形式更新 P;必要时给P 做对称化、下限裁剪。
-
镜像/旋转错位:多来自起始姿态/坐标系设定错;开头用一条已知直线走校准





















 2959
2959

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








