动态规划之数字三角形备忘录解法

最新推荐文章于 2022-09-30 20:19:43 发布

原创最新推荐文章于 2022-09-30 20:19:43 发布 · 466 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#动态规划 #算法

本文介绍了一种解决数字三角形问题的经典方法——备忘录法。通过递归求解最大路径和，并利用备忘录减少重复计算，提高算法效率。

数字三角形有两大类解法，这里记录经典递归也就是暴力解法中的备忘录法，即考虑子问题重复并记录公共子问题的解。这里以ACM-数字三角形之备忘录法为例进行记录。

函数一：求最大值函数

简单的三目运算求两个数的最大值。

int max(int a,int b){
	return a>b?a:b;
}

函数二：递归函数求最大路径和

int solve(int i,int j,int n){
    if(i>n) return 0; 
    if(p[i][j]==0){
        p[i][j]=max(solve(i+1,j,n),solve(i+1,j+1,n))+a[i][j];
    }
    return p[i][j];
}

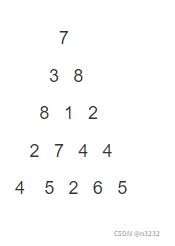如图，p[i][j]为当前的路径点，slove为路径和，当前路径和等于正下方和右下方两个路劲点的路劲和的最大值加上现在路径点的值。体现“备忘录”的部分就是对用来存路径值的数组的初始值判断，如果是初始值那就没存过，直接使用递归公式进行计算，否则直接返回数组中存的值。

完整代码：

#include<stdio.h>
#include<math.h>
#include<string.h>
int p[100][100];
int a[100][100];
	
int max(int a,int b){
	return a>b?a:b;
}
int solve(int i,int j,int n){
    if(i>n) return 0;    if(p[i][j]==0){
        p[i][j]=max(solve(i+1,j,n),solve(i+1,j+1,n))+a[i][j];
    }
    return p[i][j];
}

int main(void){

	int n,sum;
	
	while (scanf("%d",&n)!=EOF)
	{
		for(int i=0;i<n+1;i++)
            for(int j=0;j<=i;j++)
                    p[i][j]=0;
		for (int i = 1; i <=n; i++)
			for (int j = 1; j <=i; j++)
				scanf("%d",&a[i][j]);
		
			int r = solve(1,1,n);
			printf("%d\n",r);

		
				
			
		}
		return 0;
	}