LeetCode 2002. Maximum Product of the Length of Two Palindromic Subsequences【枚举/DFS】

本文属于「征服LeetCode」系列文章之一，这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁，本系列将至少持续到刷完所有无锁题之日为止；由于LeetCode还在不断地创建新题，本系列的终止日期可能是永远。在这一系列刷题文章中，我不仅会讲解多种解题思路及其优化，还会用多种编程语言实现题解，涉及到通用解法时更将归纳总结出相应的算法模板。

为了方便在PC上运行调试、分享代码文件，我还建立了相关的仓库：https://github.com/memcpy0/LeetCode-Conquest。在这一仓库中，你不仅可以看到LeetCode原题链接、题解代码、题解文章链接、同类题目归纳、通用解法总结等，还可以看到原题出现频率和相关企业等重要信息。如果有其他优选题解，还可以一同分享给他人。

由于本系列文章的内容随时可能发生更新变动，欢迎关注和收藏征服LeetCode系列文章目录一文以作备忘。

Given a string s, find two disjoint palindromic subsequences of s such that the product of their lengths is maximized. The two subsequences are disjoint if they do not both pick a character at the same index.

Return the maximum possible product of the lengths of the two palindromic subsequences.

A subsequence is a string that can be derived from another string by deleting some or no characters without changing the order of the remaining characters. A string is palindromic if it reads the same forward and backward.

Example 1:

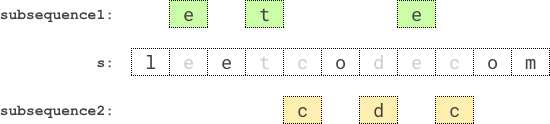
Input: s = "leetcodecom"
Output: 9
Explanation: An optimal solution is to choose "ete" for the 1st subsequence and "cdc" for the 2nd subsequence.
The product of their lengths is: 3 * 3 = 9.

Example 2:

Input: s = "bb"
Output: 1
Explanation: An optimal solution is to choose "b" (the first character) for the 1st subsequence and "b" (the second character) for the 2nd subsequence.
The product of their lengths is: 1 * 1 = 1. 

Example 3:

Input: s = "accbcaxxcxx"
Output: 25
Explanation: An optimal solution is to choose "accca" for the 1st subsequence and "xxcxx" for the 2nd subsequence.
The product of their lengths is: 5 * 5 = 25.

Constraints:

• 2 <= s.length <= 12
• s consists of lowercase English letters only.

题意：给你一个字符串 s ，请你找到 s 中两个 不相交回文子序列 ，使得它们长度的 乘积最大 。两个子序列在原字符串中如果没有任何相同下标的字符，则它们是 不相交 的。请返回两个回文子序列长度可以达到的 最大乘积 。

---

解法1 枚举+动态规划

由于这道题数据范围很小，我们可以枚举每一种子序列，最多有 $2^{12}$ 种可能。我的做法比较粗糙：

• 枚举每一种子序列，用一个位向量加以表示；
• 判断这个位向量代表的子序列是否为回文序列；
• 如果不是，则返回第一步；否则得到这一位向量的长度 $le{n}_1$ ，再取反这一位向量，选取其他剩下的字符；
• 用动态规划求出剩下的字符中，最长的回文序列的长度 $le{n}_2$ ；
• 取所有 $le{n}_1\times le{n}_2$ 中的最大值，即为题目所需结果。

整个算法的时间复杂度为 $O(2^n\times (n+n^2))$ ：

//C++ version
class Solution {
private:
    int solve(const string& s) {
        if (s.empty()) return 0; //判断是否为空
        int n = s.size();
        vector<vector<int>> dp(n, vector<int>(n));
        for (int i = n - 1; i >= 0; --i) {
            for (int j = i; j < n; ++j) {
                if (i == j) dp[i][i] = 1;
                else if (i + 1 == j) dp[i][j] = (s[i] == s[j] ? 2 : 1);
                else dp[i][j] = max(
                        max(dp[i + 1][j], dp[i][j - 1]),
                        (s[i] == s[j] ? 2 : 0) + dp[i + 1][j - 1]);
            }
        }
        return dp[0][n - 1];
    }
public:
    int maxProduct(string s) {
        if (s.size() == 2) return 1;
        int n = s.size(), tot = 1 << n, ans = 0;
        for (int i = 0; i < tot; ++i) { //枚举每种可能
            bitset<12> fi;
            int len1 = 0;
            for (int j = 0; j < n; ++j) {
                if ((i >> j) & 1) {
                    fi[j] = 1;
                    ++len1;
                }
            }
            if (len1 == 0 || len1 == n) continue;
            bool flag = true;
            for (int l = 0, r = n - 1; l < r; ) { //判断是否为回文子序列
                while (l < r && fi[l] == 0) ++l;
                while (l < r && fi[r] == 0) --r;
                if (l < r) {
                    if (s[l] == s[r]) { ++l, --r; continue; }
                    else { flag = false; break; }
                }
            }
            if (!flag) continue; //这个不是回文序列
            bitset<12> se = ~fi; //取反,看哪个没有选
            string temp;
            for (int j = 0; j < n; ++j)
                if (se[j]) temp += s[j];
            int len2 = solve(temp); //找到se中temp的最长回文子序列
            ans = max(ans, len1 * len2);
        }
        return ans;
    }
};
//执行用时：88 ms, 在所有 C++ 提交中击败了50.00% 的用户
//内存消耗：26.7 MB, 在所有 C++ 提交中击败了50.00% 的用户

属实是暴力典范了，不过比起某些dalao来说还不够。上述代码中，枚举每一种可能的子序列，判断是否为回文子序列，不是则继续枚举——这种做法排除了许多错误方案，降低了算法的复杂度。不然直接枚举每种可能的子序列，取反得到另一子序列，然后分别计算两个子序列中最长的回文序列长度，复杂度大概是 $O(2^n\times (2n^2))$ 。不列出dalao的代码，只看一下运行效率，我只能说dalao手速太快、不拘小节：

执行用时：860 ms, 在所有 C++ 提交中击败了50.00% 的用户
内存消耗：273.6 MB, 在所有 C++ 提交中击败了50.00% 的用户

---

解法2 DFS暴力搜索

暴力DFS字符串 s ，对每个字符要么不选、要么插入字符序列 a 、要么插入字符序列 b 。到达字符串尾部时，分别判断字符序列 a, b 是否为回文序列，是则取这些长度乘积的最大值作为答案。 时间复杂度大概为 $O(3^n\times n)$ ，好处是代码比较简洁、空间效率较高：

//C++ version
class Solution {
private:
    int ans = 0, n;
    bool isPindrome(const string& s) {
        for (int l = 0, r = s.size() - 1; l < r; ++l, --r)
            if (s[l] != s[r]) return false;
        return true;
    }
    void dfs(int cur, const string& s, string& a, string& b) {
        if (cur == n) {
            int an = a.size(), bn = b.size();
            if (an * bn <= ans) return;
            if (isPindrome(a) && isPindrome(b)) ans = an * bn; //是回文序列且长度乘积更大
            return;
        }
        dfs(cur + 1, s, a, b);
        a.push_back(s[cur]); dfs(cur + 1, s, a, b); a.pop_back();
        b.push_back(s[cur]); dfs(cur + 1, s, a, b); b.pop_back();
    }
public:
    int maxProduct(string s) {
        n = s.size();
        string a, b;
        dfs(0, s, a, b);
        return ans;
    }
};
//执行用时：244 ms, 在所有 C++ 提交中击败了50.00% 的用户
//内存消耗：5.9 MB, 在所有 C++ 提交中击败了100.00% 的用户