Polygon zkEVM zkProver基本设计原则以及 Storage状态机

原创已于 2023-03-23 14:51:51 修改 · 1.1k 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#zkVM

于 2023-03-21 15:46:48 首次发布

zkVM 专栏收录该内容

146 篇文章

订阅专栏

文章详细介绍了PolygonzkEVM的zkProver设计，包括基于状态机的证明系统和zkASM语言。zkProver通过处理批量交易证明其有效性，降低交易确认时间和gas费。Storage状态机作为二级状态机，负责数据存储操作，使用PIL语言和多项式承诺方案确保计算正确性。文章还深入讨论了SMT（稀疏默克尔树）的实现，包括READ、UPDATE、CREATE和DELETE操作，以及如何通过多项式约束验证计算的正确性。

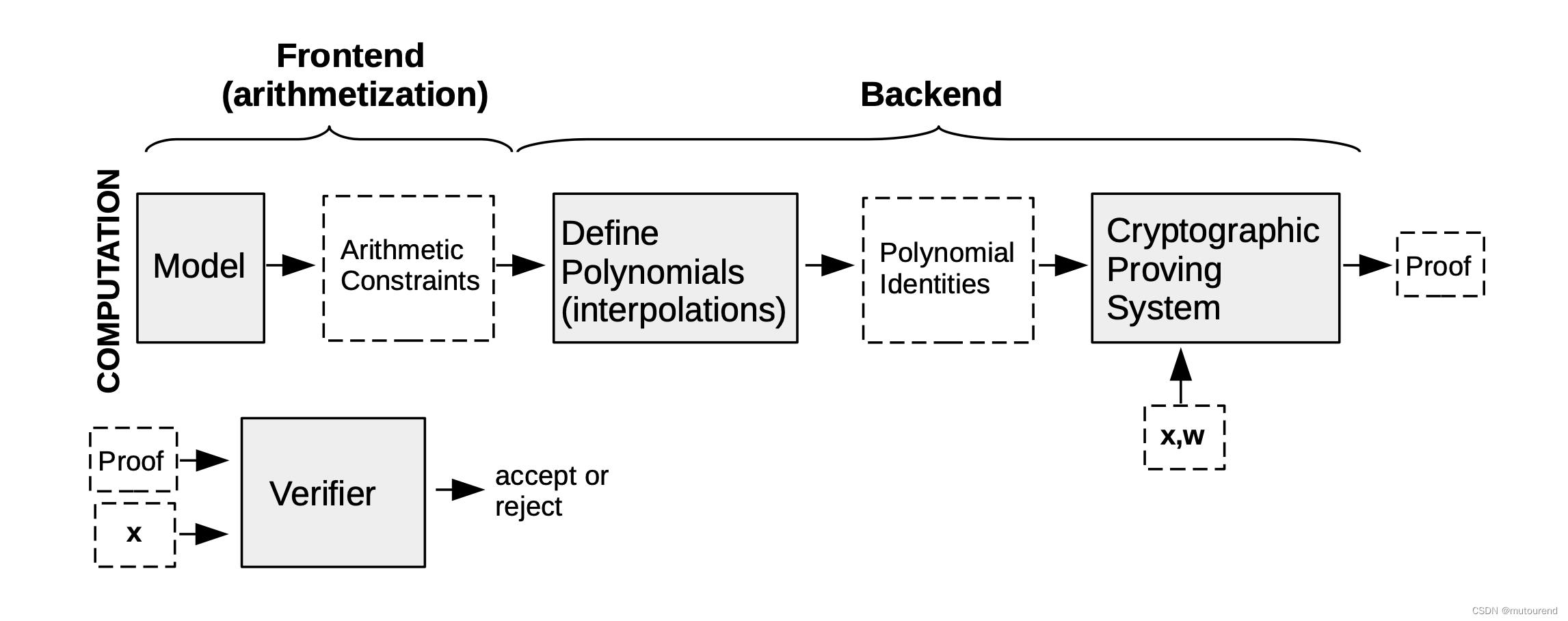
1. zkProver基本设计原则

Polygon zkEVM采用状态机模型来模拟EVM（Ethereum Virtual Machine），从而提供与以太坊相同的用户体验，并支持部署运行相同的以太坊智能合约。

Polygon zkEVM zkRollup扩容策略在于：

开发zkProver，输入a batch of many transactions，证明该batch内所有交易的有效性，然后仅发布最小化size的validity proof供验证。从而可降低交易固化时间，并为以太坊用户节约gas费。
采用前沿工具来提供可验证proof，如Polynomial Identity Language（PIL）。

状态机最适合迭代确定性计算，确定性计算在以太坊中很常见。而算术电路将需要展开loop，从而导致不希望的更大的电路。

基于状态机所实现的zkProver证明系统基本设计原则为：

1）将所需的确定性计算转换为state machine computation。
2）将state transitions以arithmetic constraints描述，arithmetic constraints为每个state transition必须遵循的规则。
3）使用state values interpolation 来构建描述状态机的多项式。
4）定义所有state values必须满足的polynomial identities。
5）某特定的密码学证明系统（如STARK、SNARK或二者结合），用于生成任何人都可验证的verifiable proof。

以上前四步通常称为Arithmetization：

对应STARKs，为Algebraic Intermediate Representation（AIR）
对应SNARKs，为R1CS

同时，由于zkProver部署的上下文为某公钥密码学系统，还需要一种承诺方案。zkProver证明计算正确性并允许任何独立方验证validity proof能力的基础是多项式承诺方案。

在这里插入图片描述

2. Storage状态机

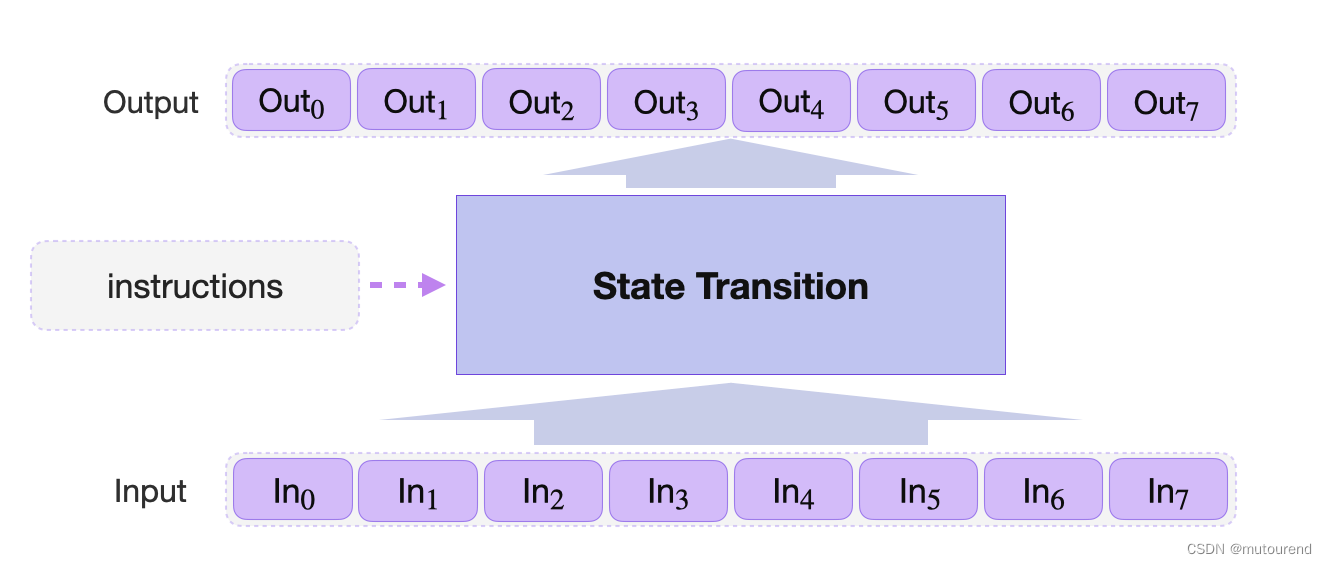
在这里插入图片描述
标准状态机为：

将一组状态存储于寄存器中作为输入
instructions：表示状态变化的规则
将结果状态存储于相同的寄存器中，作为输出。

Storage状态机为zkProver的二级状态机之一，负责存储于zkProver storage的所有数据操作：

接收来自主状态机的instructions，该instructions又称为Storage Actions。
主状态机会运行常规的数据库操作：增删改查（CRUD），然后然后指示Storage状态机验证这些操作是否正确执行。

Polygon zkEVM的Storage状态机类似于一个微处理器，具有：

1）firmware部分：包含了逻辑和规则，以JSON形式存储于某ROM中。zkASM（zero-knowledge Assembly）为Polygon zkEVM团队专门开发的语言，用于将来自主状态机的instructions map到其它状态机，本文中，即map到Storage状态机的Executor中。
主状态机的instructions或Storage Actions，会解析到 Storage状态机的Executor中，以便按照JSON文件中指定的规则和逻辑执行。
2）hardware部分：采用PIL（Polynomial Identity Language）。几乎所有的状态机都将计算以多项式表示。状态机内的state transitions必须满足特定的computation-specific polynomial identities。

为了使Storage状态机执行Storage Actions，其Executor生成committed多项式和constant多项式，然后根据多项式恒等式对其进行检查，以证明计算是正确执行的。

小结：

1）下文中的增删改查操作，即为主状态机让 Storage状态机执行的action。
2）下文中的Prover，对应为Storage状态机的Executor。
3）下文中的Verifier，对应为Storage状态机的PIL代码。
4）zkASM为Storage状态机与主状态机之间的interpreter。
5）zkASM为Storage状态机与 POSEIDON状态机之间的interpreter。
6）Storage binary SMT中所用到的2个哈希函数 $H_{\text{leaf}}，H_{\text{noleaf}}$ 为POSEIDON哈希族中的2个特定版本的哈希函数。

2.1 zkProver的SMT

前序博客有：

为实现zero-knowledge，所有的数据都存储于Merkle tree中，即意味着Storage SM（State Machine，状态机）需常向其它状态机——Poseidon SM，发送请求（POSEIDON Actions），来执行哈希运算。

key-value数据存储在SMT（Sparse Merkle Tree）中，主状态机基于这些存储在SMT中的key-value数据进行计算。key和value均以256bit string表示，也可解析为256-bit unsigned integers。

zkProver的SMT为Merkle Tree 与 Patricia Tree的结合。
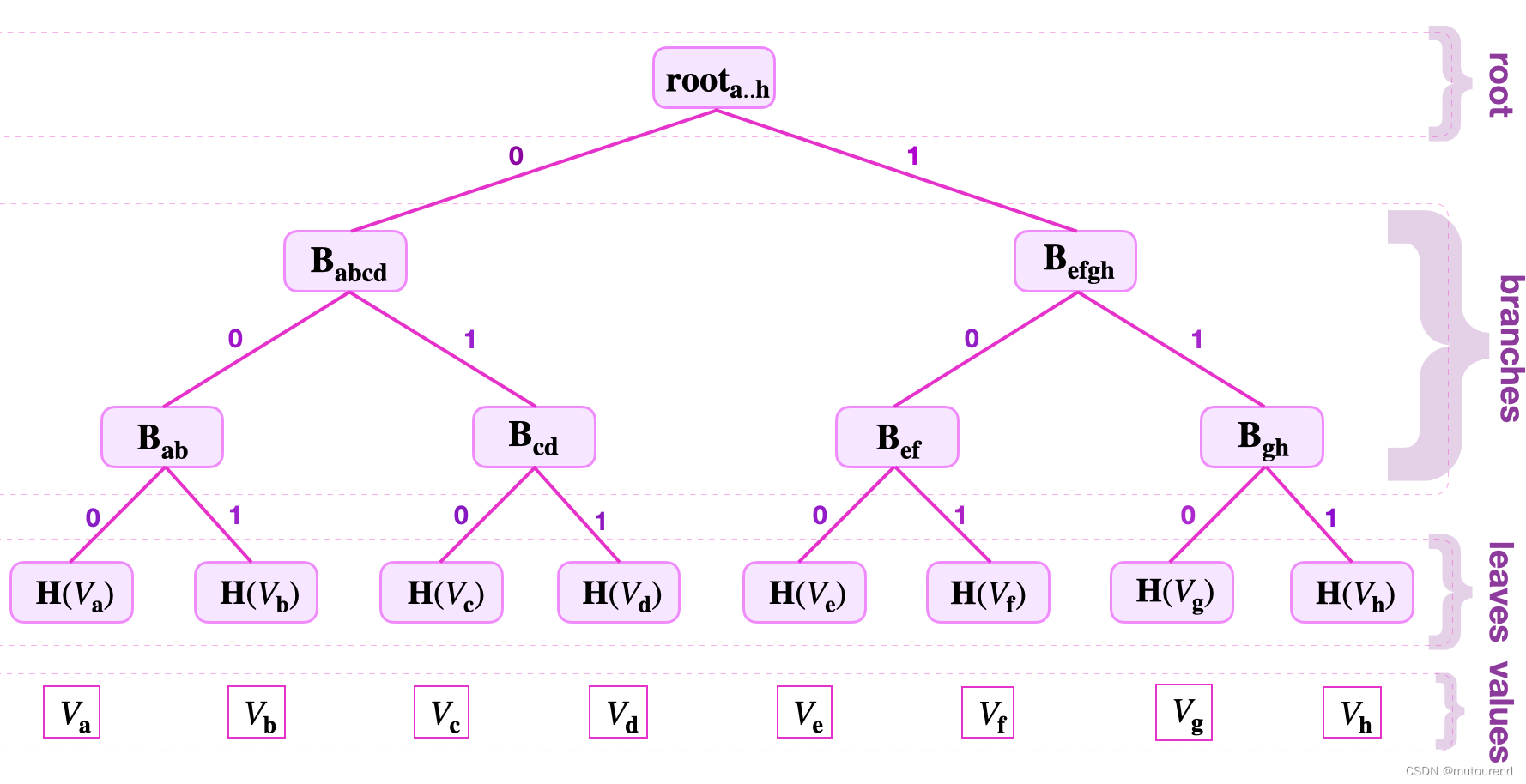
在这里插入图片描述

2.1.1 基于key-value pair的binary SMT

以8-bit key length为例。NULL SMT或 empty SMT 的root为0，即在其中未记录任何key或value。zero node或NULL node，意味着该node中国无任何value。key会决定binary SMT的形状。【所谓binary，是指其path上的label只能为0或1。】

在binary SMT中，其branches要么为leaf，要么为zero-node。

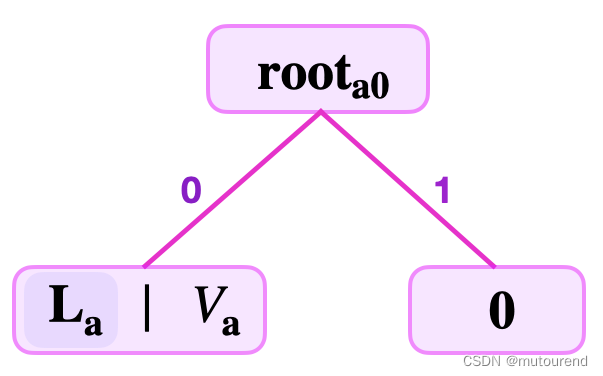
如只有一个key-value pair $K_a,V_a)$ 的binary tree，从 $K_a$ 最低有效位起，逐bit代表从root到leaf的分支选择，0表示左侧，1表示右侧。若 $K_a=11010110$ ，对应的binary SMT为：【最低有效位为0，置于左侧，zero-node置于右侧， $L_a=H(V_a)$ 。若最低有效位为1，则置于右侧，不过 $(root_{a0}=H(L_a||0))\neq (root_{0a}=H(0||L_a))$ ，分别表示的是不同的binary tree。】

在这里插入图片描述
若binary SMT中具有2个key-value pair，则，要根据其自最低有效位起，哪个bit不同来摆放。如最低2个有效位都相同，第三个才不同，则摆放情况类似为：

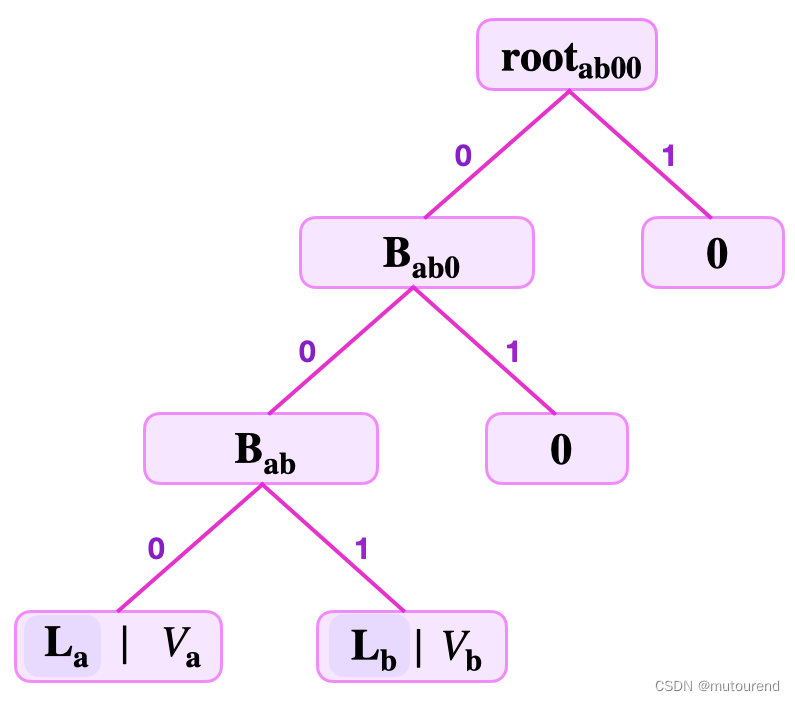
leaf level：表示某leaf到root的深度。如上图： $\text{lvl}(L_a)=3$ 。SMT中最大的leaf level决定了SMT的height。

SMT中所有的key具有相同的固定的key-length，SMT的最大height为该fixed key-length。

2.1.2 不同于通用SMT之处

不同于通用SMT之处：

leaf node $L_x$ 中不仅存储了value $V_x$ ，还存储了自root到 $L_x$ 所未使用的key-bits。这些未使用的key-bits称为remaining key，表示为 $RK_x$ 。

假设某SMT由7个key-value pair，相应的key分别为：
$K_a =10101100,K_b =10010010,K_c =10001010,K_d =11100110,K_e =11110101,K_f=10001011,K_g =00011111$
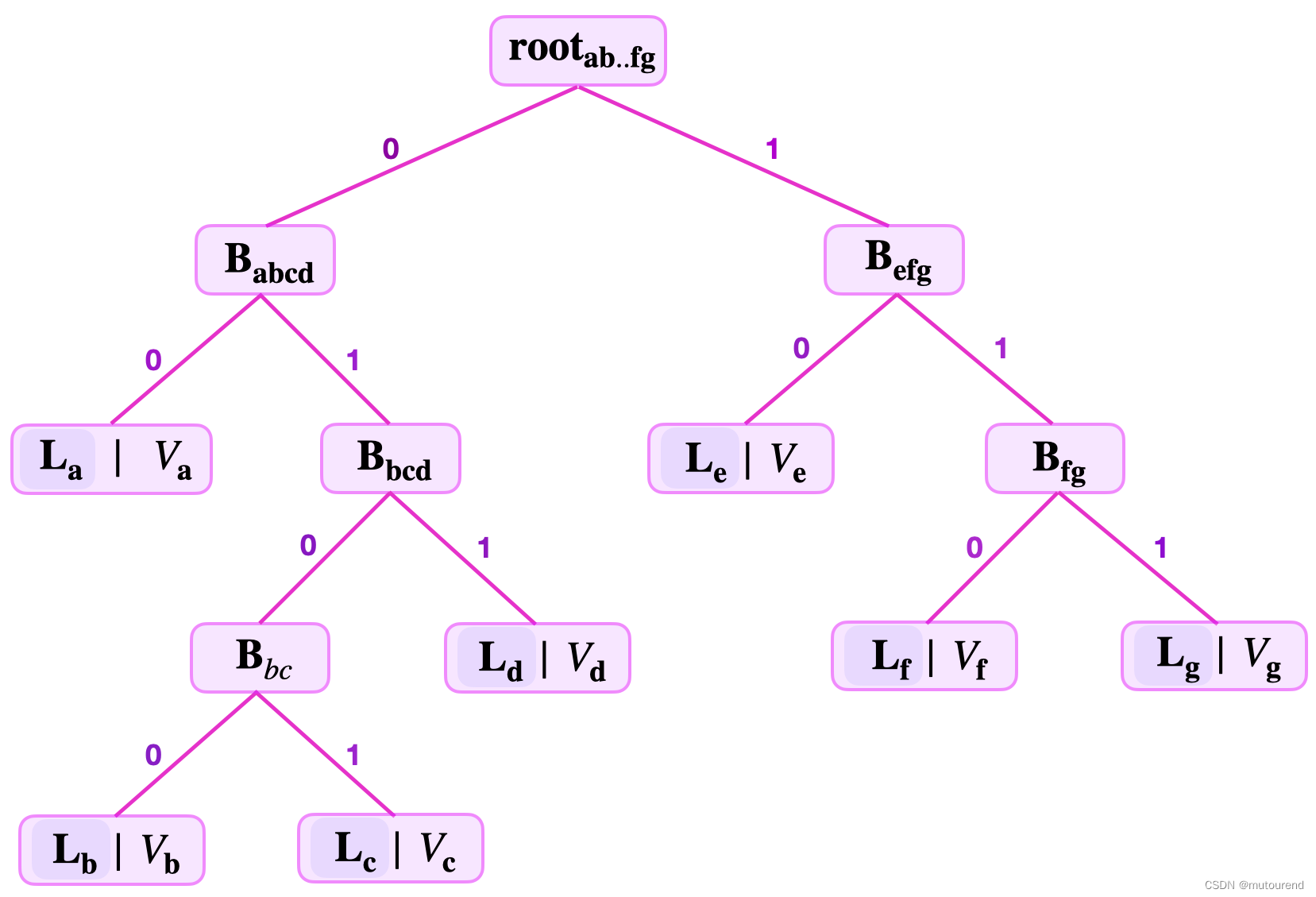
在这里插入图片描述
以上图7 leaf SMT为例，相应的Remaining key分别为：
$RK_a =101011,RK_b =1001,RK_c =1000,RK_d =11100,RK_e =111101,RK_f=10001,RK_g =00011$

2.1.3 Fake-Leaf攻击及其解决方案

至此，由于SMT中的leaf具有不同的深度，leaf和branch node采用相同的哈希函数，会存在fake-leaf攻击问题：
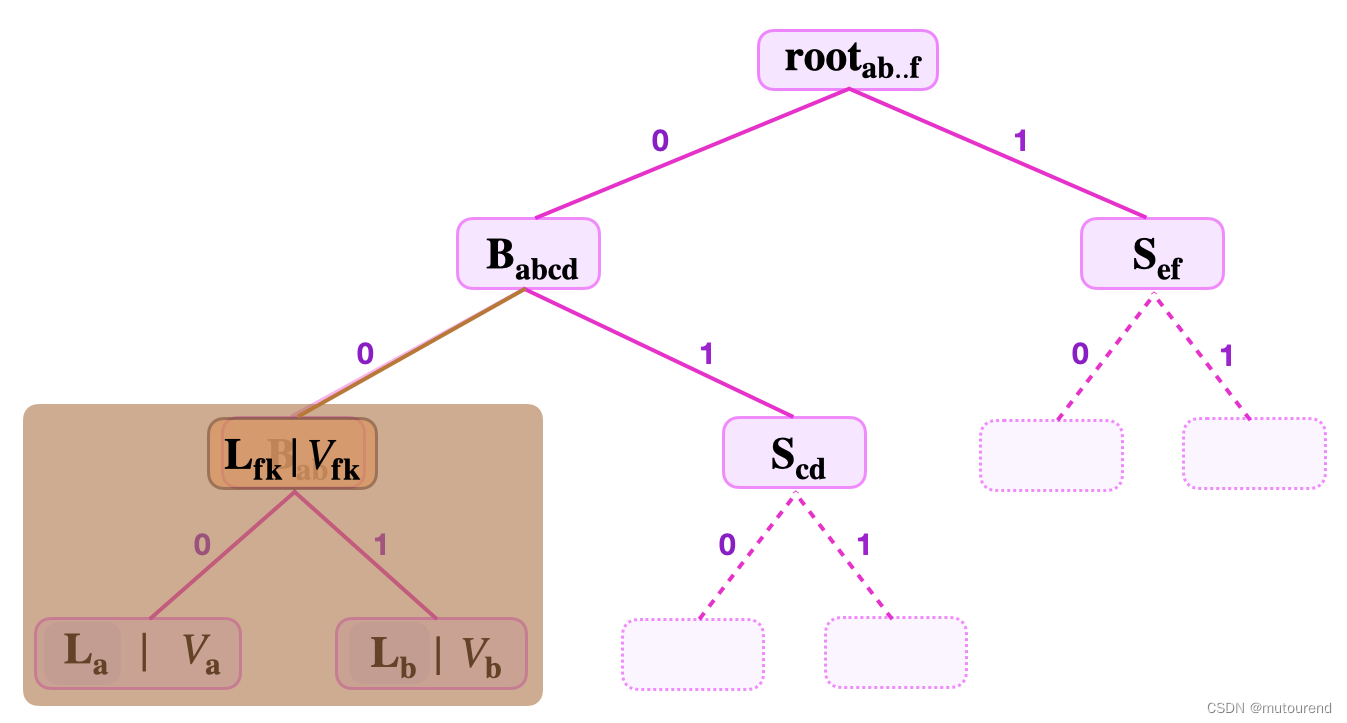
在这里插入图片描述

解决方案为，leaf和branch node采用不同的哈希函数，进行区分，使得：
$B_{ab}=H_{\text{noleaf}}(L_a||L_b)\neq H_{\text{leaf}}(L_a||L_b)=\tilde{L}_{fk}$

从而，在未知 $L_a,V_a,L_b,V_b$ 的情况下，无法以 $L_{fk},V_{fk}$ 来欺骗Verifier。

2.1.3 key-value pair Non-binding问题及其解决方案

至此，若SMT中有leaf $K_d,V_d)$ ，Malicous prover可以SMT中不存在的leaf $K_x,V_x)$ ，其中 $V_x=V_d$ ，让Verifier误以为 $K_x,V_x)$ 存在与SMT中：
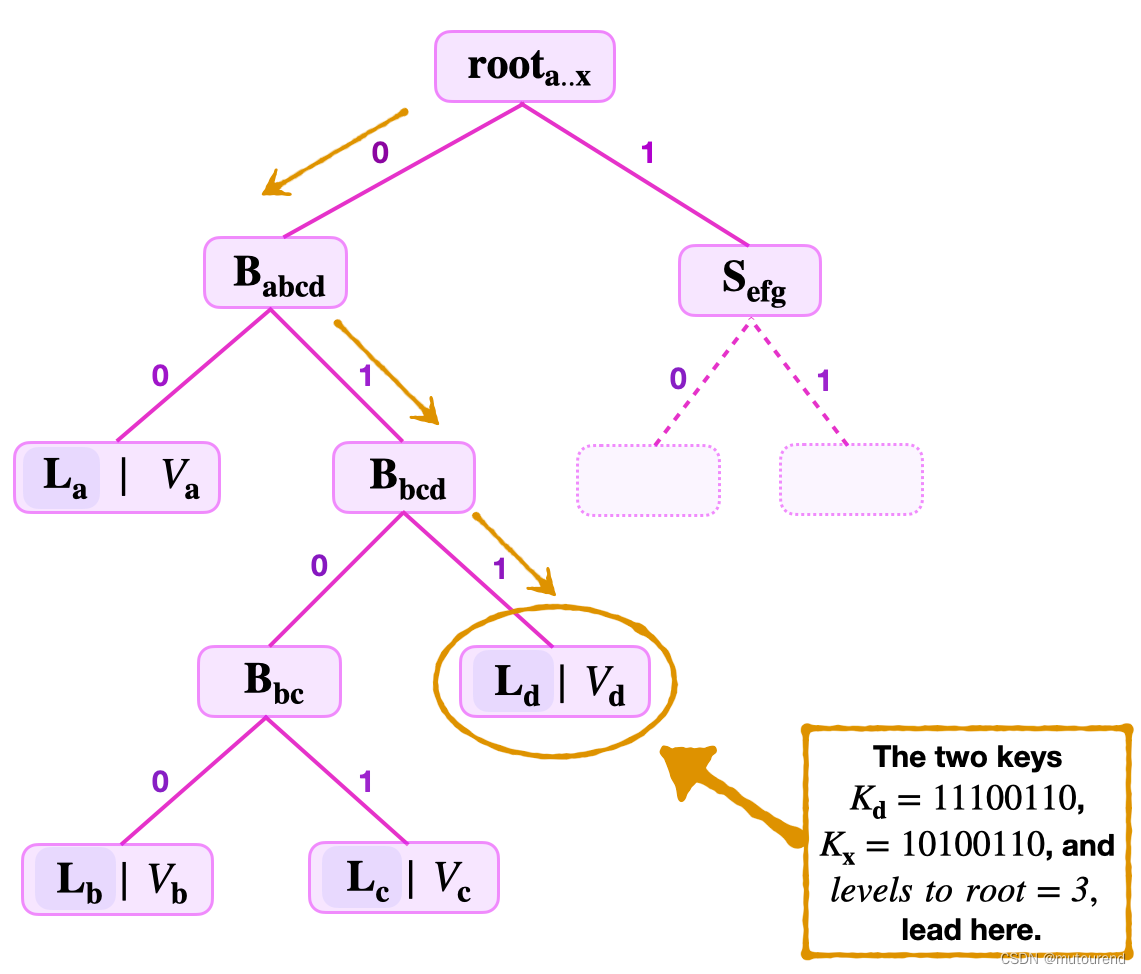
在这里插入图片描述
引起该问题的根本原因在于，key-value pair中的key与value未实现binding。相应的解决方案有：

1）将整个key-value包裹进leaf的哈希函数中： $L_x=H_{\text{leaf}}(K_x||V_x)$
2）只将remaining key和value包裹进leaf的哈希函数中： $L_x=H_{\text{leaf}}(RK_x||V_x)$

方案2）更优的原因在于，Verifier在验证merkle proof时，仅需要知悉更短的remaining key。

2.1.4 引入zero-knowledge属性

至此，key pair $K_x,V_x)$ 的leaf $L_x$ 表示为：
$L_x=H_{\text{leaf}}(RK_x||V_x)$

将value $V_x$ 以明文存储在leaf $L_x$ 中，Verifier验证Merkle proof时需知道相应的value值，为实现zero-knowledge属性，可改为在leaf中存储的是 $V_x$ 的哈希值（采用不同于leaf的哈希函数 $H_{\text{noleaf}}$ ）：
$\text{Hashed Value}=\text{HV}_x=H_{\text{noleaf}}(V_x)$ 【从而将value值 $V_x$ 隐藏在了 $\text{HV}_x$ 中了。】
$L_x=H_{\text{leaf}}(RK_x||\text{HV}_x)$

2.2 基于SMT的基本操作

Storage状态机执行的操作称为Storage Actions，Storage状态机负责验证主状态机所执行的增删改查操作是否正确。

2.2.1 READ/Get 操作

Prover：

对key-value pair $(K_x,\text{HV}_x)$ 进行commit，其中 $\text{HV}_x$ 为value $V_x$ 的哈希值，
然后声称其创建的leaf $L_x$ 包含了value $V_x$ ，且位置由key $K_x$ 决定。

Prover需给Verifier提供，即，Verifier需要知道：

1）SMT的root
2）定位leaf $L_x$ 的key-bits $\text{kb}_j$
3）Remaining Key $RK_x$
4）Merkle proof

$\text{READ}(K_x)$ 操作有2种结果：【目的是证明相应的 $K_x$ 在SMT中未设置】

返回zero node：仅需要向Verifier证明该zero-node存在于SMT中，即可证明SMT中未设置相应的key。
返回现有的leaf：需证明该leaf存在于SMT中，同时该leaf对应的key 不等于 所查询的key。

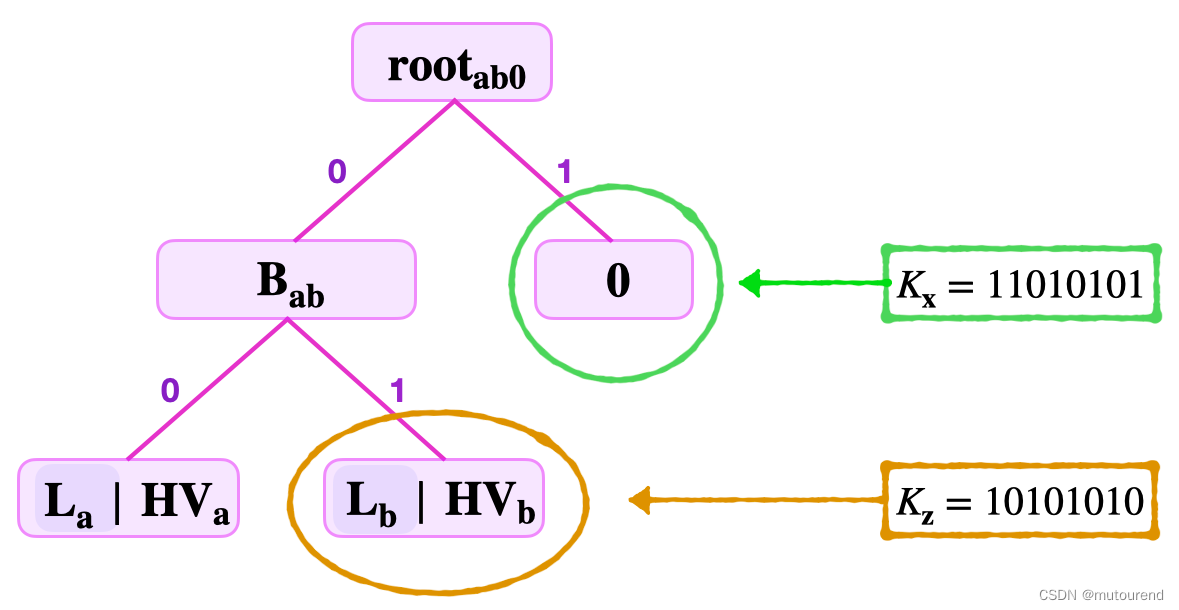
在这里插入图片描述

2.2.2 UPDATE操作

UPDATE操作不会改变SMT树的形状。因此，在执行UPDATE时，保留节点的所有labels是很重要的。

UPDATE(key)操作的基本流程为：

1）给Verifier提供如下数据，即：
- remaining key $R K$
- least-significant key-bits
- 更新后的new_value值
- 更新前的old_value值
- 更新前的old_root
- 更新前相应key的merkle proof
2）基于更新前的old_root和更新前的old_value值，执行READ(key)操作，检查相应的leaf存在于old_root对应的SMT树中。仅当本环节验证通过后才进入下一环节。
3）从所更新的key对应的leaf开始到 root，重新计算更新后，该路径上的所有节点的值，最终计算出新的root值。

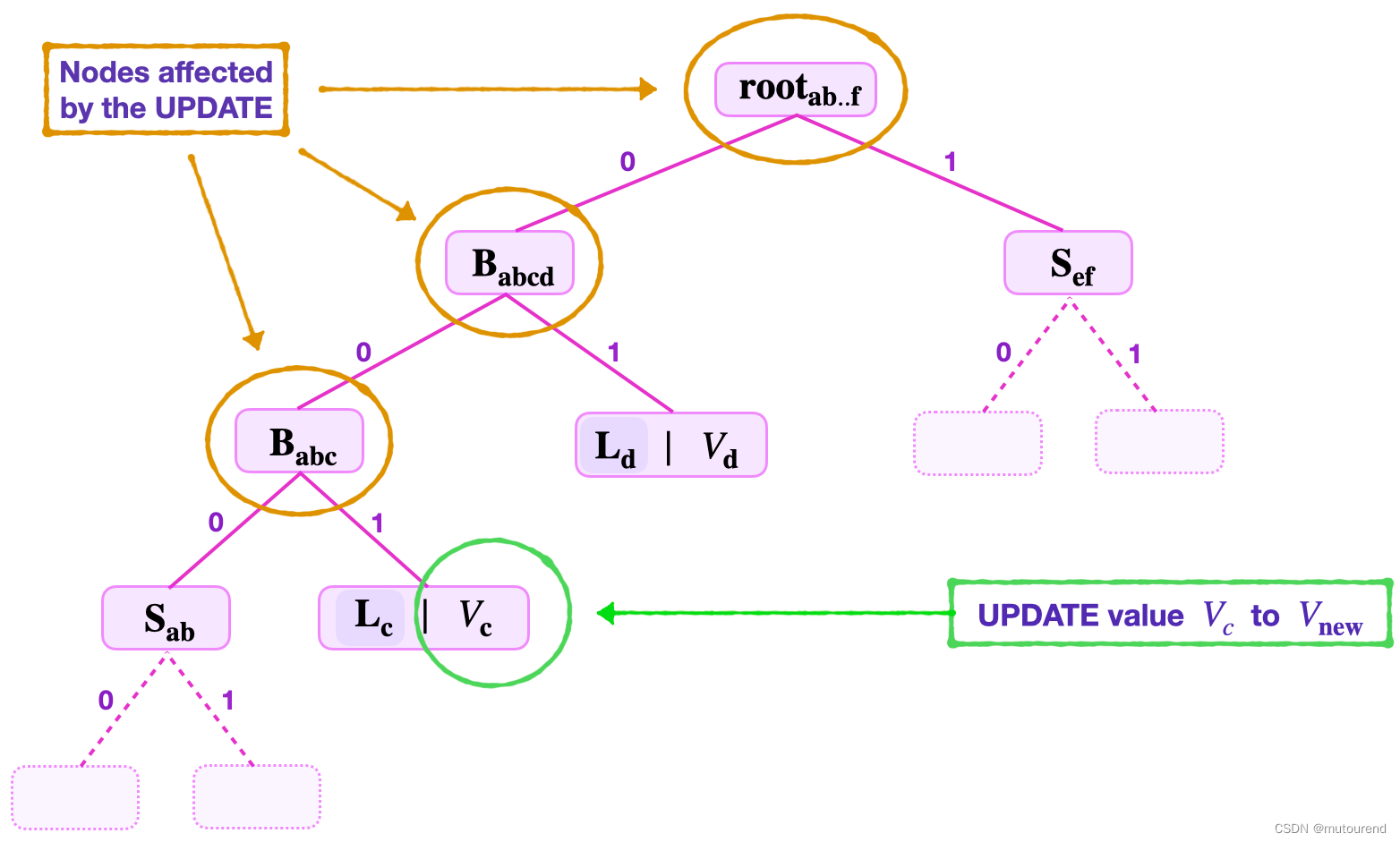
在这里插入图片描述

2.2.3 CREATE操作

CREATE操作会向SMT中插入新 leaf $L_{new}$ ，并在 leaf $L_{new}$ 中存储新的 key-value pair $K_{new}, V_{new})$ ，要求：

key $K_{new}$ 之前从未在SMT中使用
从而使得 key $K_{new}$ 唯一关联到 leaf $L_{new}$

实际CREATE操作有2种情况：

1）若新key $L_{new}$ 自root开始，指向zero node，即 CREATE Operation at a Zero Node：
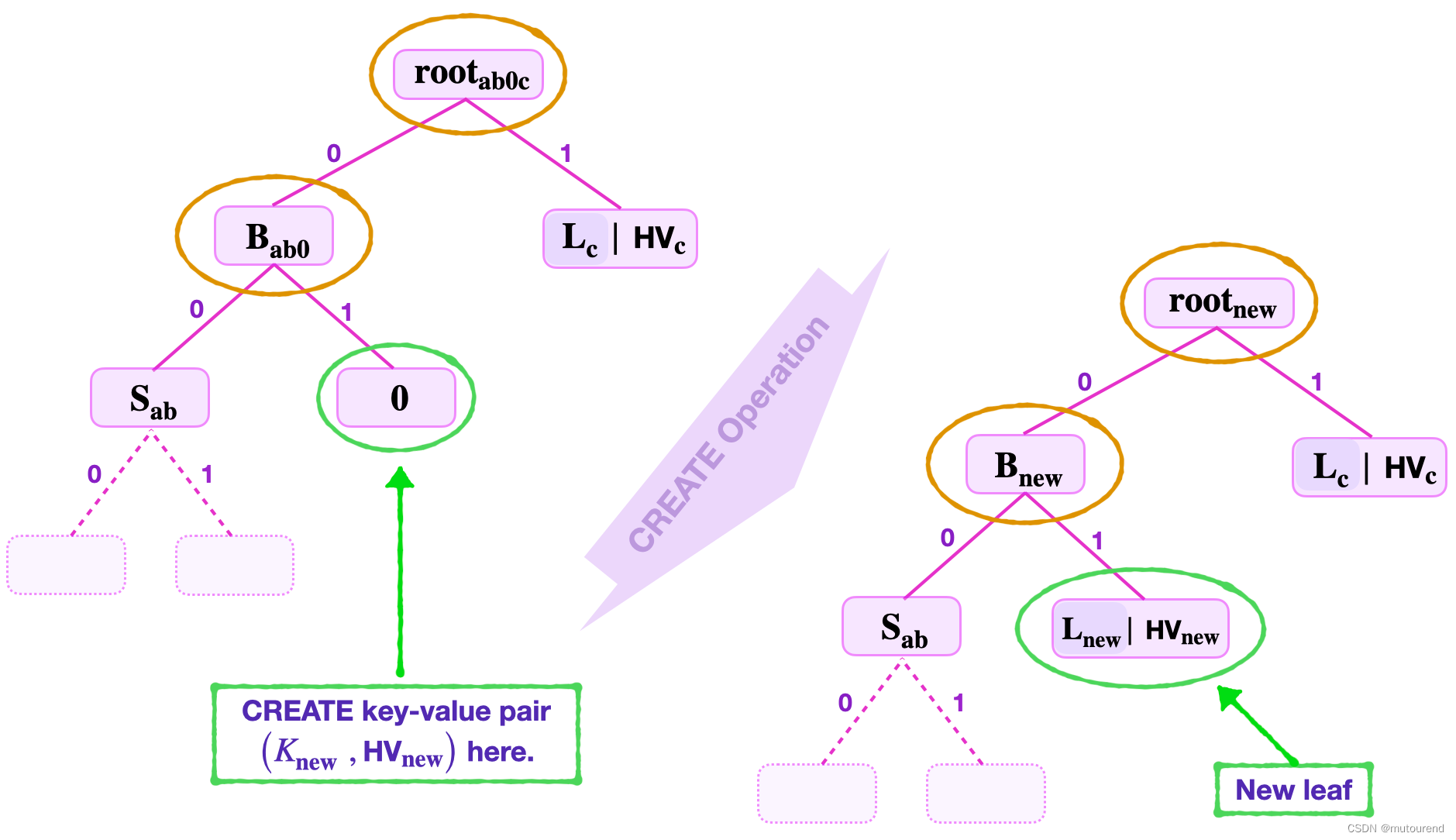
2）若新key $L_{new}$ 自root开始，指向Non-Zero leaf $L_z$ ，则：
- 2.1）Value-Inclusion Check：需检查Non-Zero leaf $L_z$ 中存储的value $V_z$ 确实包含在SMT的root中。
- 2.2）New Leaf Insertion：需为 $L_z$ 和 $L_{new}$ 创建新的branch $B_{ext1}$ 。【有可能需要插入多个branch extension】
- 2.3）UPDATE of SMT Values：自新branch向上到root，依次更新路径上的值。

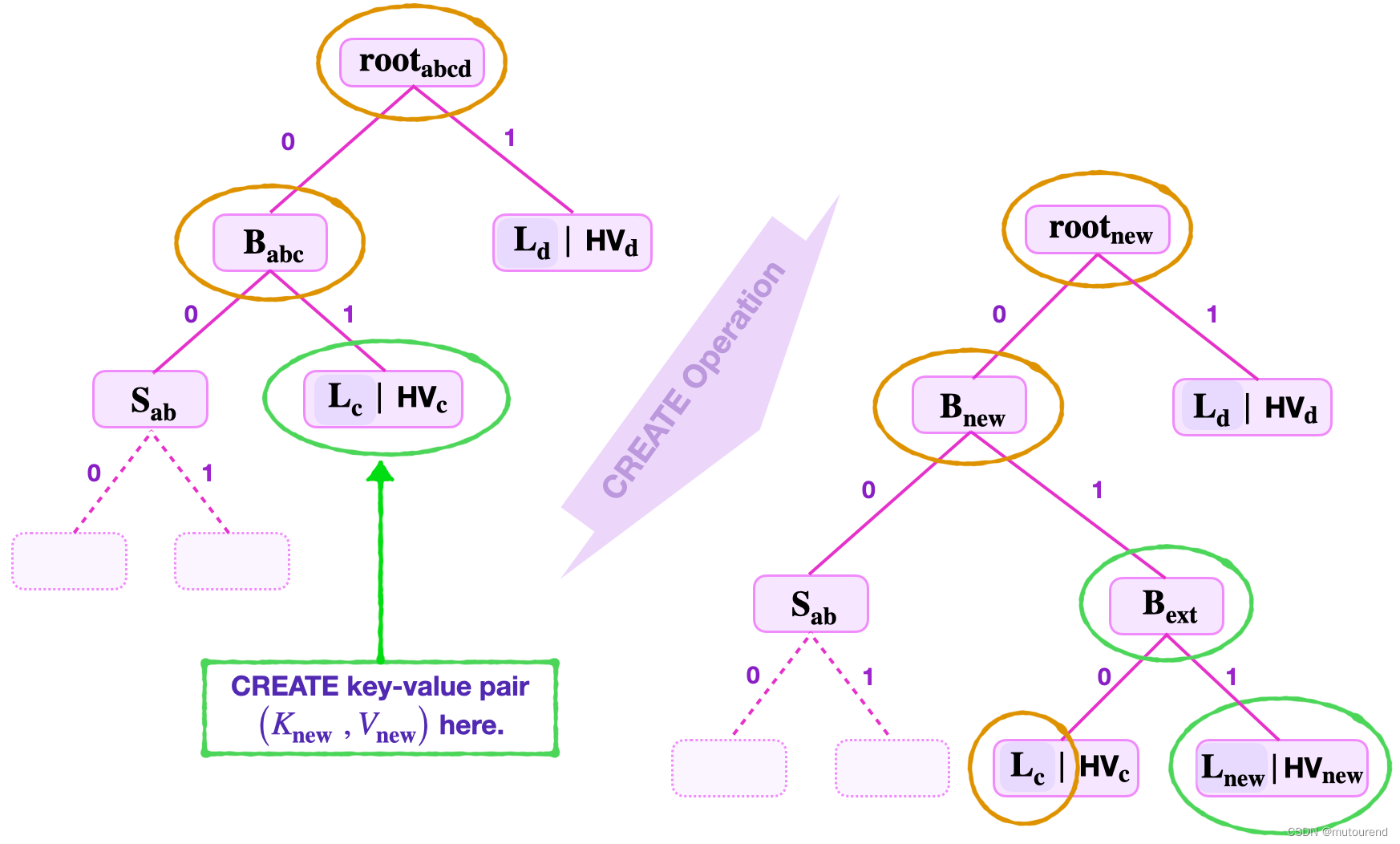
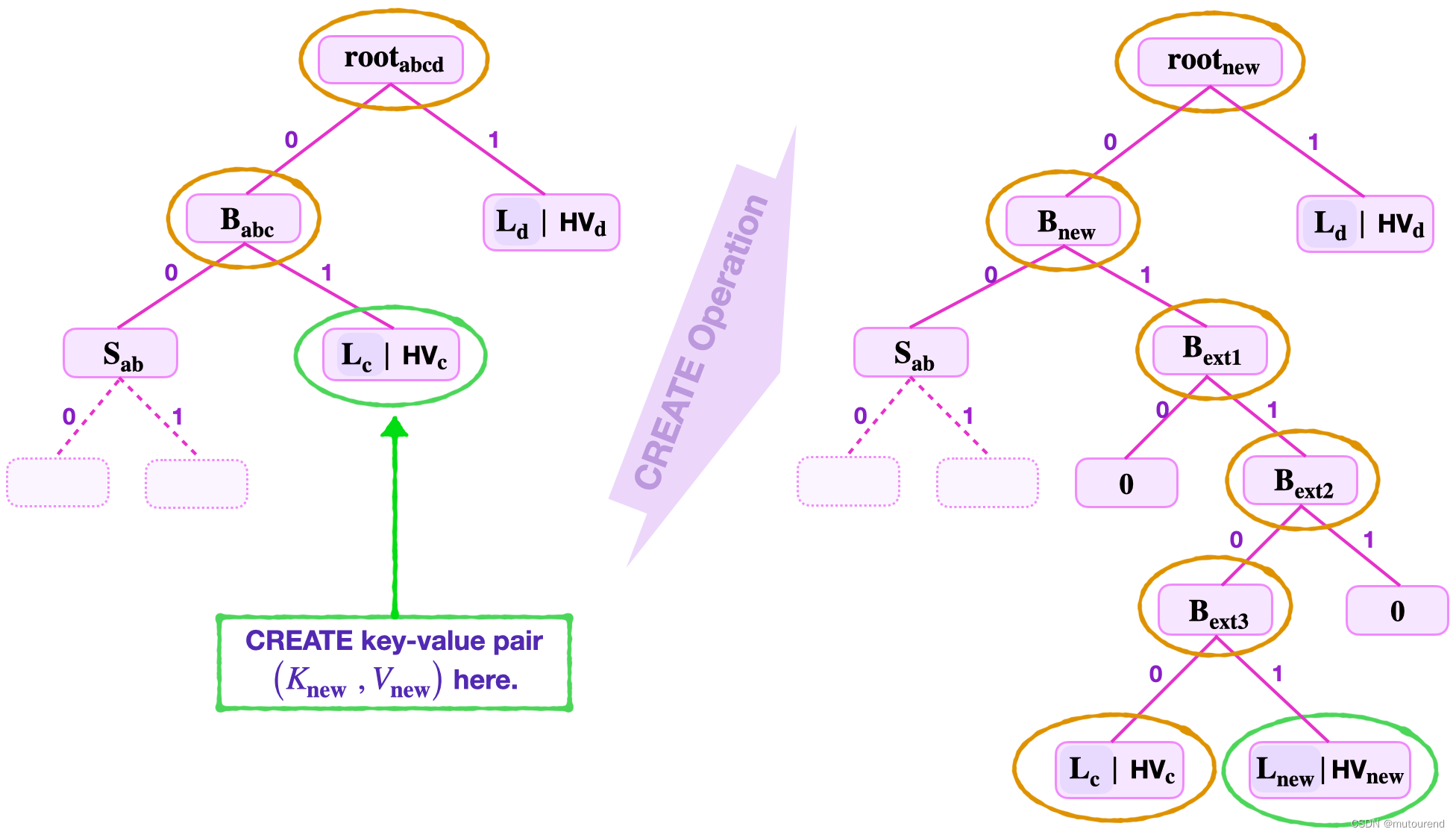
2.2.4 DELETE操作

DELETE操作是指从binary SMT中移除某特定的key-value pair，为CREATE的反向操作。

DELETE操作有2种情况：

1）等价为将某non-zero leaf UPDATE 为 NULL leaf。此时SMT的形状不会改变。当所删除的leaf具有non-zero sibling-node时，对应此场景。
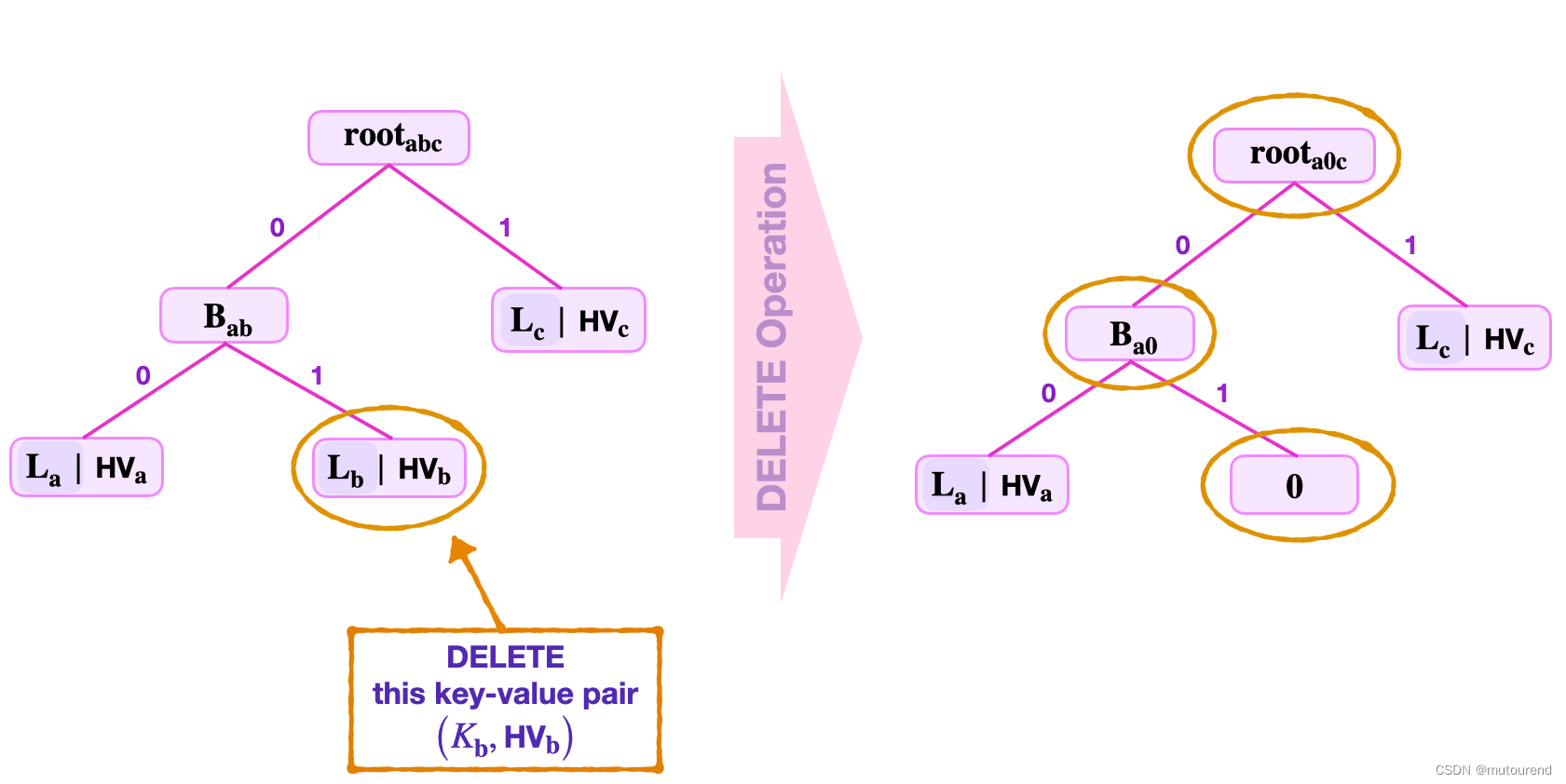
2）等同于CREATE的反向操作。需要从树中移除extension branches，数的形状会改变。当所删除的leaf具有zero sibling-node时，对应此场景。

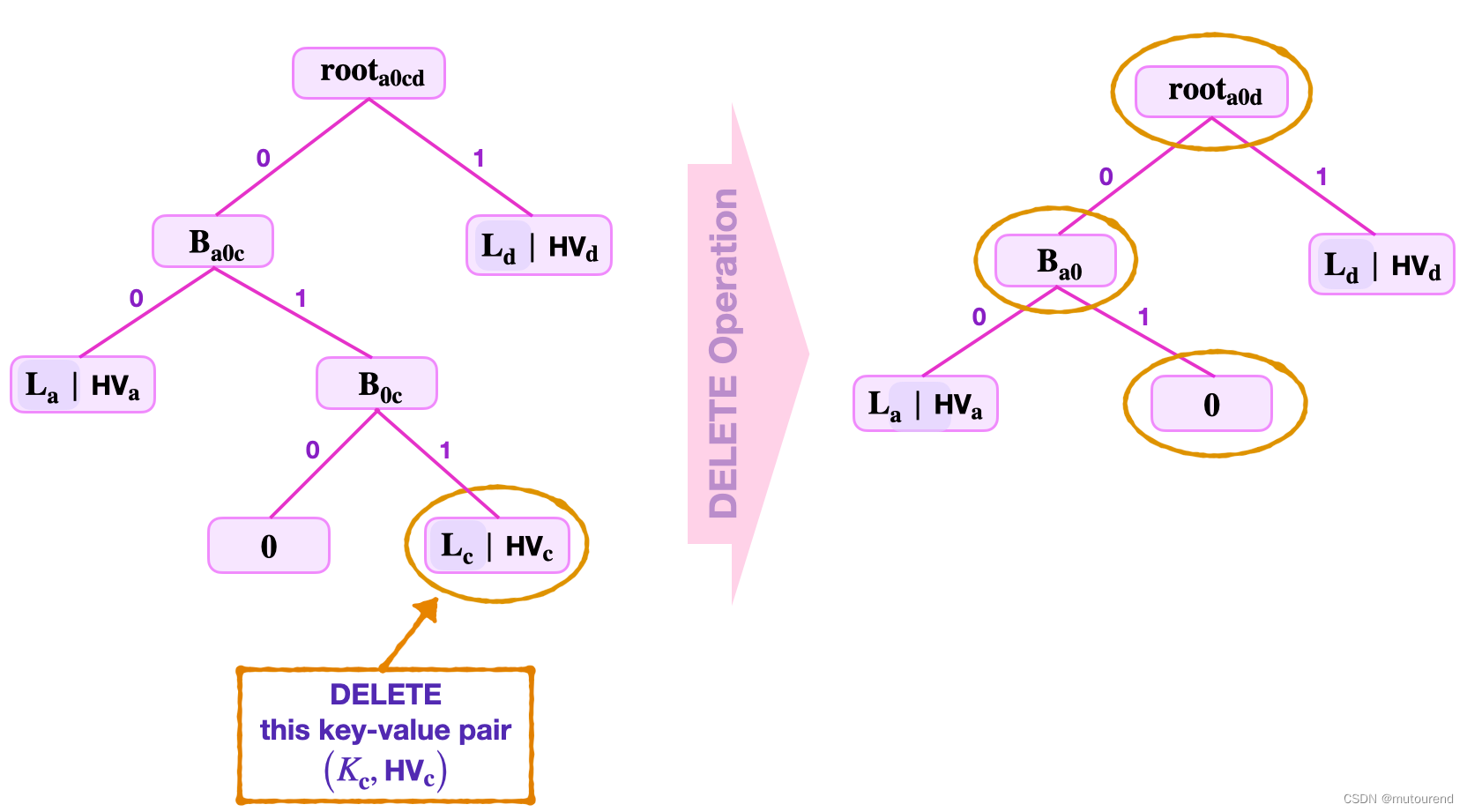
2.3 zkProver的Storage参数

在Storage状态机中，所有的key和value均为256 bits string：

可将key表示为256-bit unsigned integers，对应为4个64-bit field elements：
$\text{Key}_{0123}=(\text{Key}_0,\text{Key}_1,\text{Key}_2,\text{Key}_3)$
其中每个 $\text{Key}_i\in\mathbb{F}_p$ ，其中 $p=2^{64}-2^{32}+1$
committed values，也为256-bit long，但由于POSEIDON状态机惯例，将其表示为8个32-bit值，即：
$V_{01..7}=(V_0,V_1,V_2,\cdots,V_7)$
除committed values之外的values，以4个64-bit field elements表示。

2.3.1 Storage SMT中的key生成方式

在Storage状态机中设计的key-value pair SMT上下文中，key可唯一标识leaf，leaf的values会变化，但key不变。

因此，key必须确定性的生成，且不存在碰撞问题。key与leaf之间存在一一对应关系。采用抗碰撞哈希函数来生成key，是个不错的选择。用于生成key的哈希函数参数有：

以太坊地址
以及某些常数

为此，引入了POSEIDON哈希函数来生成key。【实际上，key=POSEIDON_HASH(account_address, storage_slot, query_key)。】

2.3.2 Storage SMT中的path表示

由于Storage SMT中的key采用4个64-bit field elements表示，因此，其path为自root到指定leaf，分别取各个field element的最低有效位、次低有效位等等来组成path：
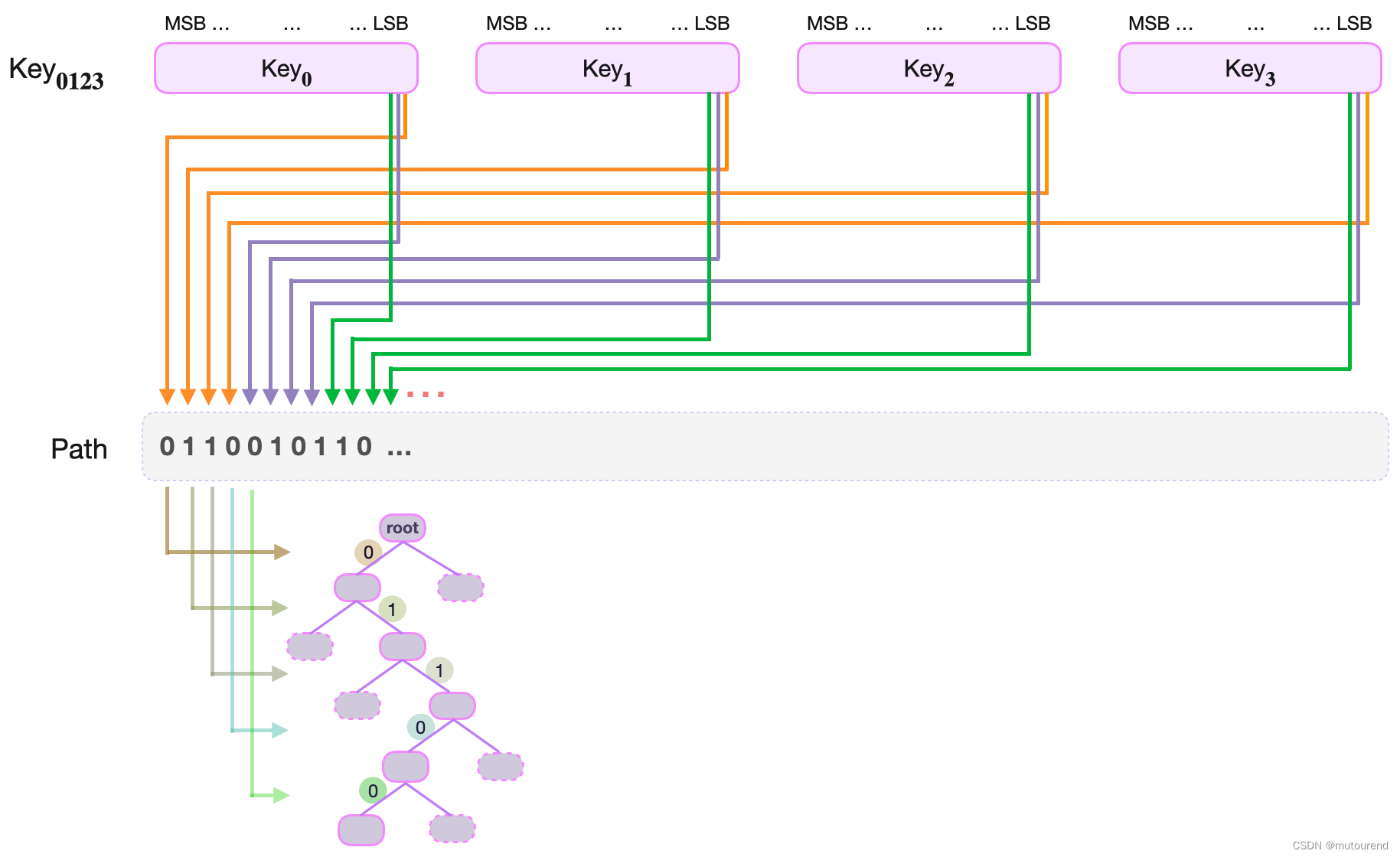
在这里插入图片描述

2.3.3 根据path-bits重构key

当做UPDATE等操作时，需要根据remaining key和path-bits重构出完整的key，这实际为 2.3.2节的反向操作。

实际实现时，为避免做modulo 4运算（因将key以4个元素来表示），引入了 1个寄存器和 1个操作：

在Storage SM中引入LEVEL寄存器：由4个bits组成，其中3个bit为0，1个bit为1。LEVEL寄存器的初始值为 $(1, 0, 0, 0)$ 。
在Storage ROM中引入ROTATE_LEVEL opcode：每次对 LEVEL寄存器进行左移1位的rotation。【当每次Prover需要climb the tree时，会使用ROTATE_LEVEL opcode。】
执行4次ROTATE_LEVEL操作，结果保持不变：
$(1, 0, 0, 0) \to (0, 0, 0, 1) \to (0, 0, 1, 0) \to (0, 1, 0, 0) \to (1, 0, 0, 0)$

可利用LEVEL寄存器来进行key重构：
在这里插入图片描述

2.4 Storage状态机机制

Storage状态机设计为微处理器，由3部分组成：

Storage Assembly code
Storage Executor code
Storage PIL code

2.4.1 Storage Assembly code

Storage Assembly code 为主状态机与 Storage Executor之间的 interpreter：

Storage状态机接收到的主状态机指令是以zkASM编写的
然后生成包含相应规则和逻辑的JSON文件
该JSON文件作为Storage状态机的特殊ROM。

Storage状态机中具有primary Storage Assembly code，来将主状态机的指令，映射为，对应每个基本操作的secondary Assembly code。
这些基本操作主要为本文之前提到的CREATE\READ\UPDATE\DELETE操作。

Storage状态机中主要有8种secondary Assembly code，详情见：https://github.com/0xPolygonHermez/zkevm-storage-rom/tree/main/zkasm，具体的映射关系为：

Storage Actions	File Names	Code Names	Action Selectors In Primary zkASM Code
READ	Get	Get	isGet()
UPDATE	Set_Update	SU	isSetUpdate()
CREATE new value at a found leaf	Set_InsertFound	SIF	isSetInsertFound()
CREATE new value at a zero node	Set_InsertNotFound	SINF	isSetInsertNotFound()
DELETE last non-zero node	Set_DeleteLast	SDL	isSetDeleteLast()
DELETE leaf with non-zero sibling	Set_DeleteFound	SDF	isSetDeleteFound()
DELETE leaf with zero sibling	Set_DeleteNotFound	SDNF	isSetDeleteNotFound()
SET a zero node to zero	Set_ZeroToZero	SZTZ	isSetZeroToZero()

Storage状态机的输入和输出状态均为SMT，形如：

Merkle roots
relevant siblings
key-value pairs

不过状态机中采用的为寄存器，而不是变量。基本操作所需的所有值，均存储在primary Assembly code的如下寄存器中：

HASH_LEFT, HASH_RIGHT, OLD_ROOT, NEW_ROOT, VALUE_LOW, VALUE_HIGH, SIBLING_VALUE_HASH, RKEY, SIBLING_RKEY, RKEY_BIT, LEVEL.

其中SIBLING_VALUE_HASH和SIBLING_RKEY这2个寄存器仅由 Set_InsertFound和Set_DeleteFound 这2个secondary Assembly code使用。其余的寄存器则被所有secondary Assembly code使用。

primary Assembly code 借助 selectors 来将主状态机指令转换为相应的Storage Actions。selectors要么为0，要么为1：

1表示该action被选中执行
0表示指令与相应action 不符，即应用JMPZ（“Jump if zero”）

2.4.2 Storage Executor code

Storage Executor类似于a slave-worker to the master，此处master，是指the Storage Assembly code。Executor根据Assembly code中所定义的规则和逻辑来执行所有的Storage Actions。

对于主状态机中的每个指令，借助之前提到的secondary Assembly code selectors，Storage Executor会调用以JSON文件存储的Storage ROM 中的特定secondary Assembly code函数。相应的函数有：

GetSibling(), GetValueLow(), GetValueHigh(), GetRKey(), GetSiblingRKey(), GetSiblingHash(), GetSiblingValueLow(), GetSiblingValueHigh(), GetOldValueLow(), GetOldValueHigh(), GetLevelBit(), GetTopTree(), GetTopBranch() 以及 GetNextKeyBit()

2.4.3 Storage PIL code

Storage中所执行的所有计算都必须是可verifiable的，因此引入了PIL code来建立Verifier所需的所有多项式约束，以验证执行的正确性。

这些多项式约束是自Storage Executor开始准备的。为此，Storage Executor使用了：

selectors
setters
instructions

这些均为Boolean多项式，具体的Boolean committed多项式有：

Selectors	Setters	Instructions
selFree[i]	setHashLeft[i]	iHash
selSiblingValueHash[i]	setHashRight[i]	iHashType
selOldRoot[i]	setOldRoot[i]	iLatchSet
selNewRoot[i]	setNewRoot[i]	iLatchGet
selValueLow[i]	setValueLow[i]	iClimbRkey
selValueHigh[i]	setValueHigh[i]	iClimbSiblingRkey
selRkeyBit[i]	setSiblingValueLow[i]	iClimbSiblngRkeyN
selSiblingRkey[i]	setSiblingValueHigh[i]	iRotateLevel
selRkey[i]	setRkey[i]	iJmpz
	setSiblingRkey[i]	iConst0
	setRkeyBit[i]	iConst1
	setLevel[i]	iConst2
		iConst3
		iAddress