题目链接:http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemCode=3696
文章转自:http://www.cnblogs.com/Duahanlang/archive/2013/05/07/3065472.html
There's an alien whose name is Marjar. It is an universal solder came from planet Highrich a long time ago.
Marjar is a strange alien. It needs to generate new organs(body parts) to fight. The generated organs will provide power to Marjar and then it will disappear. To fight for problem of moral integrity decay on our earth, it will randomly generate new fighting organs all the time, no matter day or night, no matter rain or shine. Averagely, it will generate λ new fighting organs every day.
Marjar's fighting story is well known to people on earth. So can you help to calculate the possibility of that Marjar generates no more than N organs in one day?
Input
The first line contains a single integer T (0 ≤ T ≤ 10000), indicating there are T cases in total. Then the following T lines each contains one integer N (1 ≤ N ≤ 100) and one float numberλ (1 ≤ λ ≤ 100), which are described in problem statement.
Output
For each case, output the possibility described in problem statement, rounded to 3 decimal points.
Sample Input
3 5 8.000 8 5.000 2 4.910
Sample Output
0.191
0.932
0.132
解题思路:泊松分布:
泊松分布的概率质量函数为:
泊松分布的参数 λ 是单位时间(或单位面积)内随机事件的平均发生率。
泊松分布的数学期望和方差均为 λ;
此题关键在于数学公式的感知,起初以为是正态分布,纠结了好久,没能写出来,最后还是找了下概率论的书,套了下所有觉得可能的分布,最终发现泊松分布最恰当。
此题求解的是 P(X <= K) 的概率
P(X <= K) = P(0) + P(1) + P(2) + ··· + P(K)(X= 0,1,2,…)
PS:注意阶乘太大,只能用浮点型~
//泊松分布公式P(X=k)=(e^(-p)*p^k)/(k!) p代表当前能获得的期望,k为目标获得的值。
//比如此题外星人1天能生长器官的期望是p,但是要求1天生长器官不超过k。
//p(x<=k)=p(0)+p(1)+p(2)+p(3)+....p(k)
#include <stdio.h>
#include <math.h>
int main()
{
int t,i,n;
double m;
scanf("%d",&t);
while (t--)
{
scanf("%d%lf",&n,&m);
double k=1.000;
double s=exp(-m);
for (i=1;i<=n;i++)
{
k*=(i*1.000);
s+=exp(-m)*pow(m,i)/k;
}
printf("%0.3lf\n",s);
}
return 0;
}







 本文介绍了一道使用泊松分布解决的实际问题:计算外星人Marjar一天内生成器官数量不超过N的概率。通过解析题目背景及需求,给出了具体的解题思路与C语言实现代码。
本文介绍了一道使用泊松分布解决的实际问题:计算外星人Marjar一天内生成器官数量不超过N的概率。通过解析题目背景及需求,给出了具体的解题思路与C语言实现代码。
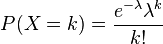
















 4019
4019

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








