K近邻算法（KNN）

最新推荐文章于 2022-10-04 17:33:07 发布

转载最新推荐文章于 2022-10-04 17:33:07 发布 · 303 阅读

文章标签：

#分类算法

算法专栏收录该内容

17 篇文章

订阅专栏

一.基本思想

K近邻算法，即是给定一个训练数据集，对新的输入实例，在训练数据集中找到与该实例最邻近的K个实例，这K个实例的多数属于某个类，就把该输入实例分类到这个类中。如下面的图：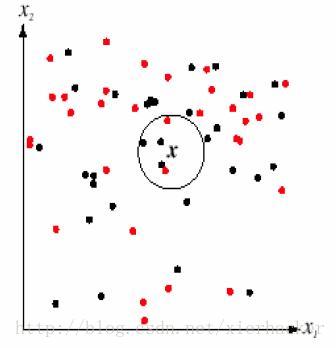
这里写图片描述
通俗一点来说，就是找最“邻近”的伙伴，通过这些伙伴的类别来看自己的类别。比如以性格和做过的事情为判断特征，和你最邻近的10个人中（这里暂且设k=10），有8个是医生，有2个是强盗。那么你是医生的可能性更加大，就把你划到医生的类别里面去，这就算是K近邻的思想。
K近邻思想是非常非常简单直观的思想。非常符合人类的直觉，易于理解。
至此，K近邻算法的核心思想就这么多了。
K值选择,距离度量,分类决策规则是K近邻法的三个基本要素.
从K近邻的思想可以知道，K近邻算法是离不开对于特征之间“距离”的表征的，至于一些常见的距离，参考：
机器学习笔记八：常见“距离”归纳

二.实战

这一部分的数据集《机器学习实战》中的KNN约会分析，代码按照自己的风格改了一部分内容。
首先是读取数据部分(data.py)：

import numpy as np 

def creatData(filename):
    #打开文件,并且读入整个文件到一个字符串里面
    file=open(filename)
    lines=file.readlines()
    sizeOfRecord=len(lines)

    #开始初始化数据集矩阵和标签
    group=np.zeros((sizeOfRecord,3))
    labels=[]
    row=0
    #这里从文件读取存到二维数组的手法记住
    for line in lines:
        line=line.strip()
        tempList=line.split('\t')
        group[row,:]=tempList[:3]

        labels.append(tempList[-1])
        row+=1
    return group,labels

然后是KNN算法的模块：KNN.py

import numpy as np 
#分类函数(核心)
def classify(testdata,dataset,labels,k):
    dataSize=dataset.shape[0]
    testdata=np.tile(testdata,(dataSize,1))
    #计算距离并且按照返回排序后的下标值列表
    distance=(((testdata-dataset)**2).sum(axis=1))**0.5
    index=distance.argsort()

    classCount={}
    for i in range(k):
        label=labels[index[i]]
        classCount[label]=classCount.get(label,0)+1

    sortedClassCount=sorted(list(classCount.items()),
        key=lambda d:d[1],reverse=True)

    return sortedClassCount[0][0]


#归一化函数(传入的都是处理好的只带数据的矩阵)
def norm(dataset):
    #sum/min/max函数传入0轴表示每列,得到单行M列的数组
    minValue=dataset.min(0)
    maxValue=dataset.max(0)

    m=dataset.shape[0]
    return (dataset-np.tile(minValue,(m,1)))/np.tile(maxValue-minValue,(m,1))


#测试函数
def classifyTest(testdataset,dataset,dataset_labels,
                testdataset_labels,k):
    sampleAmount=testdataset.shape[0]

    #归一化测试集合和训练集合
    testdataset=norm(testdataset)
    dataset=norm(dataset)
    #测试
    numOfWrong=0
    for i in range(sampleAmount):
        print("the real kind is:",testdataset_labels[i])
        print("the result kind is:",
            classify(testdataset[i],dataset,dataset_labels,k))
        if testdataset_labels[i]==classify(testdataset[i],
                                    dataset,dataset_labels,k):
            print("correct!!")
        else:
            print("Wrong!!")
            numOfWrong+=1
        print()

    print(numOfWrong)

画图模块(drawer.py)：

import matplotlib.pyplot as plt
import numpy as np 
from mpl_toolkits.mplot3d import Axes3D
import data 

def drawPlot(dataset,labels):
    fig=plt.figure(1)
    ax=fig.add_subplot(111,projection='3d')
    for i in range(dataset.shape[0]):
        x=dataset[i][0]
        y=dataset[i][1]
        z=dataset[i][2]
        if labels[i]=='largeDoses':
            ax.scatter(x,y,z,c='b',marker='o')
        elif labels[i]=='smallDoses':
            ax.scatter(x,y,z,c='r',marker='s')
        else:
            ax.scatter(x,y,z,c='g',marker='^')
    plt.show()

测试模块（run.py）

import data
import KNN 
import drawer

#这里测试数据集和训练数据集都是采用的同一个数据集
dataset,labels=data.creatData("datingTestSet.txt")
testdata_set,testdataset_labels=data.creatData("datingTestSet.txt")

print(type(dataset[0][0]))
#测试分类效果。K取得是10
KNN.classifyTest(testdata_set,dataset,labels,testdataset_labels,10)

#画出训练集的分布
drawer.drawPlot(dataset,labels)

结果：
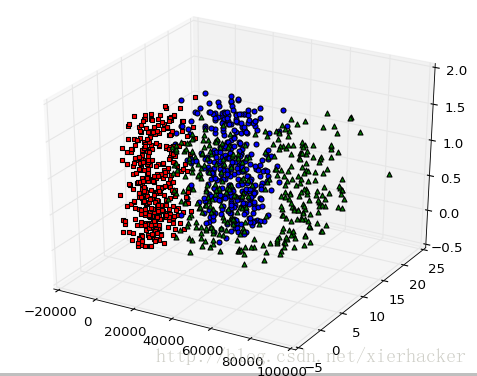
这里写图片描述

三.优缺点分析

从上面的代码可以看到，K近邻法并不具有显式的学习过程,你必须先把数据集存下来，然后类似于比对的来作比较。K近邻法实际上是利用训练数据集对特征向量空间进行划分,并且作为其分类的模型
优点：

多数表决规则等价于经验风险最小化.
精度高,对异常值不敏感,无数据输入假定

缺点：

K值选择太小,意味着整体模型变得复杂,容易发生过拟合.但是K值要是选择过大的话,容易忽略实例中大量有用的信息,也不可取.一般是先取一个比较小的数值,通常采用交叉验证的方式来选取最优的K值.

计算复杂度高,空间复杂度高

本文转载自https://blog.youkuaiyun.com/xierhacker/article/details/61914468