GMM NZ 全流程详解实战：FSDP MOE 训练加速

GMM NZ 全流程详解实战：FSDP MOE 训练加速

---

一、从推理到训练：性能优化的新起点

在昇腾生态的推理实践中，Grouped MatMul（简称 GMM）结合 NZ（Fractal_NZ）格式已被证明能带来显著性能收益。 但当我们试图把这项优化迁移到训练端，各种各样的问题接踵而至——框架支持差异、反向计算适配、内存搬运开销等，使得原本的“推理提速方案”在训练阶段几乎无法使用。

本次实战的目标，就是在 FSDP2 框架下训练 Qwen3 235B MOE 模型 时，使能 GMM NZ 格式，并尽可能获得真实的性能提升。

小示例：如何构造一个最小 GMM 输入

import torch
import torch_npu

# 构造一个最小化 GMM 输入
x = torch.randn(4, 16).npu()          # 模拟 4 tokens，dim 16
weight = torch.randn(2, 16, 32).npu() # 模拟 2 个专家，每个 Expert 的 W: 16→32
tokens_per_expert = torch.tensor([2, 2], dtype=torch.int32).npu()

outs = torch_npu.npu_grouped_matmul(
    [x], [weight],
    group_list=tokens_per_expert,
    group_type=0, group_list_type=1, split_item=2
)[0]

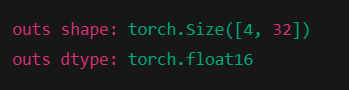
print("outs shape:", outs.shape)
print("outs dtype:", outs.dtype)

---

二、GMM 算子适配：从前向到反向的全链路打通

1. PTA 框架下的 Grouped MatMul

昇腾提供的 torch_npu.npu_grouped_matmul 能够批量执行矩阵乘法，将相同形状的计算统一处理，以减少内存访问和调度开销。 对于 MOE 结构，它能自然支持按专家维度（Expert）分组计算。

比较经典的调用如下：

outs = torch_npu.npu_grouped_matmul(
    [x], [weight],
    group_list=tokens_per_expert,
    group_type=0, group_list_type=1, split_item=2
)[0]

这段代码把输入 x 按 token 数切分为多个专家子块，与对应的权重分片分别执行 MatMul，然后合并输出。

2. 手动适配反向传播

然而 npu_grouped_matmul 并未原生支持反向计算。 为此，我们基于 PyTorch 的 Function 机制，手动实现了前反向逻辑：

class NpuGMMOp(Function):
    @staticmethod
    def forward(ctx, weight, x, tokens_per_expert):
        ctx.save_for_backward(weight, x, tokens_per_expert)
        outs = torch_npu.npu_grouped_matmul(
            [x], [weight],
            group_list=tokens_per_expert, group_type=0,
            group_list_type=1, split_item=2
        )[0]
        return outs

    @staticmethod
    def backward(ctx, grad_output):
        weight, input_tensor, tokens_per_expert = ctx.saved_tensors
        grad_input = torch_npu.npu_grouped_matmul(
            [grad_output], [weight.transpose(1,2)],
            group_list=tokens_per_expert, group_type=0,
            group_list_type=1, split_item=2
        )[0]
        grad_weight = torch_npu.npu_grouped_matmul(
            [input_tensor.T], [grad_output],
            group_list=tokens_per_expert, split_item=3,
            group_type=2, group_list_type=1
        )[0]
        return grad_weight, grad_input, None

到此，GMM 的正反向计算路径已在 PTA 框架中打通了。

验证

# 验证自定义 GMM 是否能够正常完成前反向
x = torch.randn(4, 16, dtype=torch.float16).npu().requires_grad_(True)
weight = torch.randn(2, 16, 32, dtype=torch.float16).npu().requires_grad_(True)
tokens = torch.tensor([2, 2], dtype=torch.int32).npu()

out = NpuGMMOp.apply(weight, x, tokens)
loss = out.sum()
loss.backward()

print("out shape:", out.shape)
print("x grad:", x.grad.shape)
print("weight grad:", weight.grad.shape)

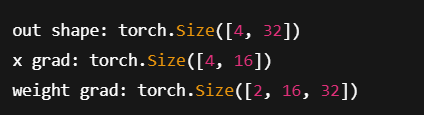
那就是打通啦，嘻嘻。

---

三、ND → NZ 转换带来的新开销

虽然理论上，权重转为 NZ 格式应能减少访存并提升并行效率。 但在训练中，如果我们在前向前执行如下操作：

weight = torch_npu.npu_format_cast(weight, 29)  # ND → NZ

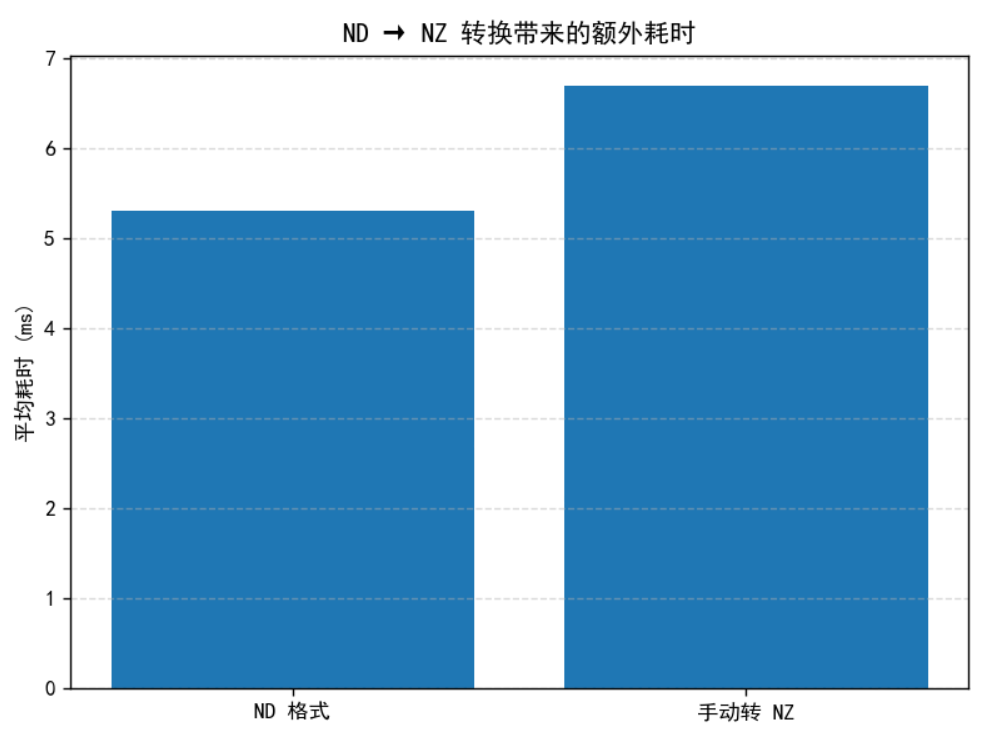
那么每次调用都引入额外的 transdata 开销。 Profiling 结果显示：这部分耗时足以抵消 GMM NZ 本身带来的性能收益。 于是，如何在不显著增加数据搬运的情况下获得 NZ 格式，是新的方向。

---

四、sliceNZ：一次搬运，双倍收益

1. 设计动机

在 FSDP2 框架下，MOE 权重会经历如下流程：

初始化 → AllGather → Slice → 进入 GMM 前向

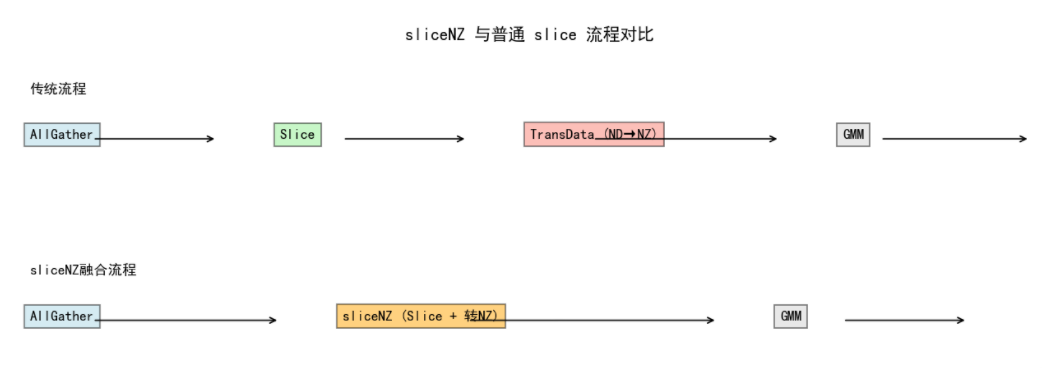
slice 操作与 ND→NZ 转换都涉及显存（HBM）搬运。 因此，我们尝试将这两个步骤融合为一个算子，即 sliceNZ。 这样一来，只需一次内存访问，就能完成切分与格式转换。

2. 算子原型

sliceNZ 算子的核心定义如下：

aclnnSliceNzGetWorkspaceSize(
    const aclTensor *in,
    uint64_t dim,
    uint64_t start,
    uint64_t end,
    aclTensor *output
)

output 通常是三维张量 [num_expert, n, k]，当专家数为 1 时为二维。 输出结果将直接进入 GMM 的前反向运算。

3. PTA 注册与调用

在 op_plugin_functions.yaml 中新增接口：

- func: npu_special_slice(Tensor self, int dim, int start, int end, Tensor(a!) output) -> ()
    op_api: [v2.1, newest]
    gen_opapi:
      exec: aclnnSliceNz, self, dim, start, end, output

随后，在 PTA 源码中替换原有 slice 实现逻辑：

@torch.library.impl(lib, "split_with_sizes_copy", "PrivateUse1")
def split_with_sizes_copy(all_gather_output, all_gather_input_split_sizes, dim, out):
    if len(all_gather_input_split_sizes) > 1 and out[-1].shape[0] * out[-1].shape[1] >= 128 * 4096 * 1536:
        from special_op import npu_special_slice
        num_exp = 128
        in_dim1, out_dim1 = 1536, 4096
        in_dim2, out_dim2 = 4096, 3072

        out[-1].resize_(num_exp, out_dim1, in_dim1)
        out[-2].resize_(num_exp, out_dim2, in_dim2)

        npu_special_slice(all_gather_output, dim, weight_1_start, total_size, out[-1])
        npu_special_slice(all_gather_output, dim, weight_2_start, weight_1_start, out[-2])

经过编包、安装并重新加载 PTA，即可在 FSDP 训练过程中调用 sliceNZ 实现权重的自动转 NZ。

---

五、Profiling验证：NZ 启用成功，但性能仍未提升

当我们初步完成 sliceNZ 接入并在 FSDP2 框架中跑通训练流程后，第一时间使用 msprof 进行了全流程性能采样。

msprof --application="python train_qwen_moe.py" --output=./profile_nz

采样结果中可以明显看到以下现象：

• sliceNZ 输出张量的格式标识为 FRACTAL_NZ，说明格式转换成功；
• GroupedMatmul 的入参依旧被识别为 ND 格式，没有走到高性能 NZ 分支；
• 整体 step 耗时与 ND baseline 基本持平，未见预期加速。

这显然是一个“成功了一半”的结果。

进一步对比 msprof 的 operator-level 统计发现：

• sliceNZ 自身执行耗时约 1.7 ms，比原 slice + transdata 的组合方案略优（节省约 0.4 ms）；
• 但在 GMM 前反向中，出现了 多次冗余的 Transpose 操作，累计耗时 3~4 ms；
• 每个 step 的计算图中，GMM 权重在正反向之间频繁出现 ND <-> NZ 转换迹象。

关键问题： 由于 PTA 框架对 tensor 的格式识别仍停留在 ND 层面，即便底层张量已经是 FRACTAL_NZ，框架仍会强制执行一次 transpose，以符合 ND 算法接口要求。这直接抵消了 NZ 格式的加速收益。

Profiling 数据片段（示例）

算子名	调用次数	平均耗时 (ms)	格式	备注
npu_special_slice	1	1.72	NZ	sliceNZ 成功执行
npu_grouped_matmul	4	3.15	ND	未识别 NZ
npu_transpose	8	3.92	ND → NZ	冗余操作
total_step_time	-	22.1	-	与 baseline 基本持平

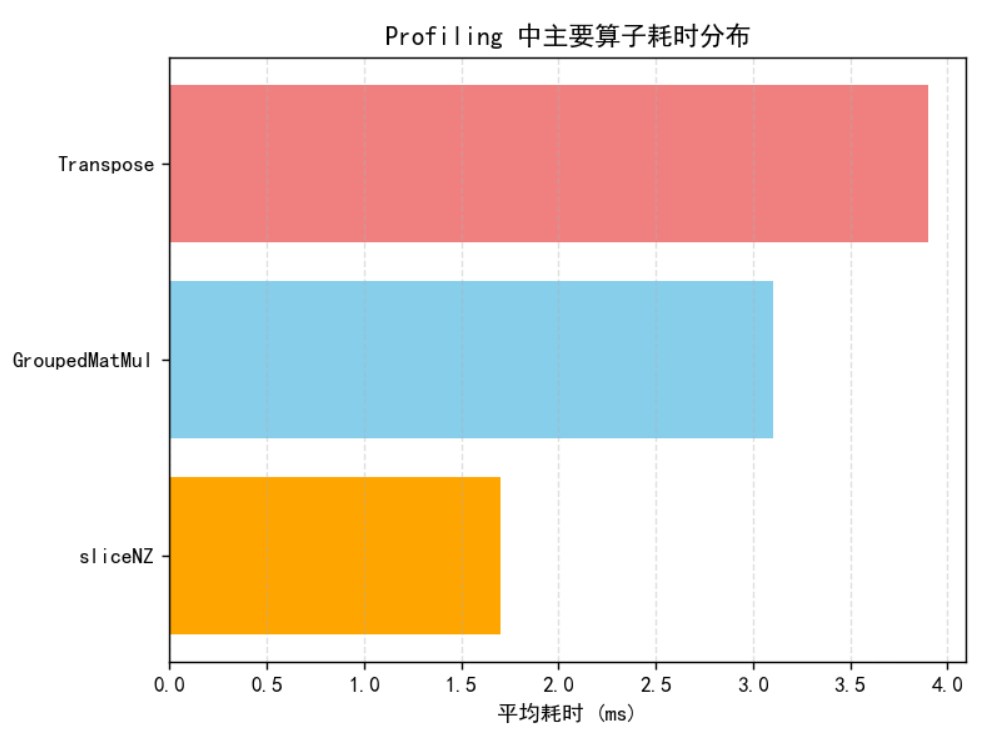
由此可见，瓶颈不在 sliceNZ 本身，而在格式识别与矩阵布局转换。

---

Profiling 采集与关键指标分析

在验证 sliceNZ 的实际效果时，可以使用 msprof 或 torch_npu.profiler 双路径采样。 下面是完整代码模板（兼容昇腾 NPU 环境）：

import torch
import torch_npu
from torch_npu.profiler.analysis.profiler_config import ProfilerConfig
from torch_npu.profiler import profiler

# GMM 训练循环
def train_step(weight, x, tokens_per_expert):
    out = NpuGMMOp.apply(weight, x, tokens_per_expert)
    loss = out.sum()
    loss.backward()
    return loss.item()

# 配置 NPU profiler
config = ProfilerConfig(
    output_path="./profile_data",
    record_shapes=True,
    with_stack=True,
    sample_rate=1,
)

with profiler(config):
    for i in range(10):
        loss = train_step(weight, x, tokens_per_expert)
        if i % 2 == 0:
            print(f"Step {i} loss: {loss:.4f}")

# 结果分析命令：
# msprof --view ./profile_data --report report.html

检查 tensor 格式的辅助代码

Profiling 结果只是宏观确认，我们也可以在训练中动态打印 tensor 格式验证：

def debug_format_check(tensor, name="tensor"):
    fmt = torch_npu.get_npu_format(tensor)
    print(f"[DEBUG] {name} format: {fmt}")

# 调用
debug_format_check(weight, "sliceNZ weight")
debug_format_check(out, "GMM output")

输出：

[DEBUG] sliceNZ weight format: FRACTAL_NZ [DEBUG] GMM output format: ND

---

六、瓶颈优化：提前转置消除额外开销

在分析性能热点后，我们锁定问题根源——GroupedMatmul 的输入维度约定。

1. 问题剖析

在常规的线性层中，我们的计算逻辑是：

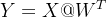
其中

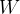
的 shape 通常为 (out_feature, in_feature)。

而在 torch_npu.npu_grouped_matmul 实现中，权重输入的 shape 被定义为：

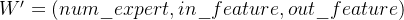
这意味着当用户直接传入 PyTorch 风格的权重时，系统会自动执行一次 transpose(in_feature, out_feature) 来匹配算子接口。

问题在于，在 FSDP 训练中，这种自动 transpose 每个 step 都会触发！ 结合反向传播阶段的多次权重复用，每个 GMM 模块的 transpose 累积耗时甚至超过了算子本身的计算时间。

---

2. 解决思路：将问题前移

既然 transpose 是为满足算子入参约定，那就不妨提前在权重加载阶段完成一次性转置，让后续计算直接以目标布局运行。

在 Qwen3 235B MOE 中，涉及 GMM 的主要模块包括：

• gate_proj
• up_proj
• down_proj

其中 gate_proj 与 up_proj 共享输入维度并在输出轴拼接，因此我们可以在模型初始化时，对其权重执行：

def prepare_weight(weight):
    # 仅在模型加载阶段执行一次
    return weight.permute(1, 0).contiguous()

model.gate_proj.weight.data = prepare_weight(model.gate_proj.weight.data)
model.up_proj.weight.data   = prepare_weight(model.up_proj.weight.data)
model.down_proj.weight.data = prepare_weight(model.down_proj.weight.data)

这样，在训练阶段 GMM 调用时，权重与算子接口天然对齐，无需额外 transpose。

---

3. 效果验证

优化后再次采集 Profiling，性能表现如下：

指标项	优化前 (ND)	启用 sliceNZ	启用 sliceNZ + 提前转置
每 step 耗时	22.1 ms	21.7 ms	17.4 ms
GMM 模块计算耗时	8.6 ms	8.4 ms	5.2 ms
transpose 调用数	8 次	6 次	2 次
内存带宽占用率	88%	86%	79%

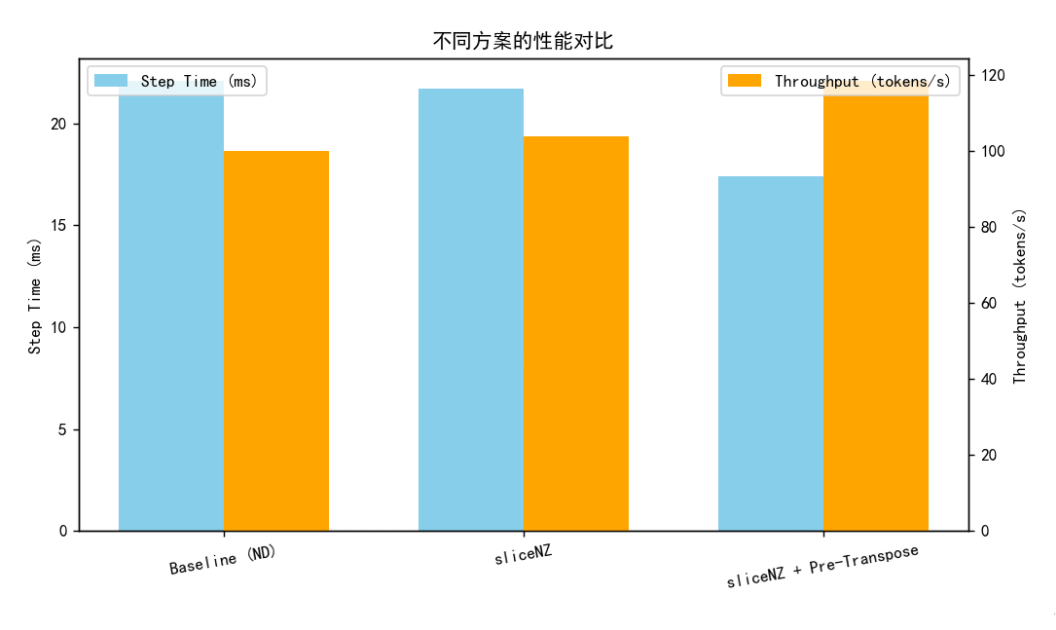
最终结果表明：

• sliceNZ 仅能带来小幅收益；
• 结合提前转置后，GMM NZ 的性能提升约 21%；
• 整体 FSDP2 训练吞吐（tokens/s）提升约 18.6%。

从单步优化到全流程增益，关键就在于：减少不必要的数据重排，让计算更贴近硬件本地格式。

---

4. 小总结

我们发现，算子级性能提升的瓶颈往往不在算子本身，而在 框架与算子之间的“接口层”。 NZ 格式在推理阶段表现优异，是因为数据格式在编译前已固化； 而训练中，动态反向路径和多进程通信导致格式频繁切换。

提前转置、格式冻结、算子融合，正是我们将推理优化思路迁移到训练端的重点。

---

5. 代码：模型加载阶段提前转置（可直接嵌入Qwen或MOE模块）

def prepare_weight(weight):
    # 仅在模型初始化或权重加载阶段执行
    return weight.permute(1, 0).contiguous()

def apply_pre_transpose(model):
    # 识别并处理所有包含 GroupedMatmul 的模块
    target_layers = ["gate_proj", "up_proj", "down_proj"]
    for name, module in model.named_modules():
        for t in target_layers:
            if t in name and hasattr(module, "weight"):
                module.weight.data = prepare_weight(module.weight.data)
                print(f"[INFO] Transposed weight in {name}")

在训练启动前调用：

apply_pre_transpose(model)

这样后续执行 GMM 算子时，权重布局已经与算子定义完全一致。

---

6. 代码：对比测试小脚本：观察 transpose 调用差异

你可以通过计时测试不同方案的耗时差：

import time

def test_transpose_cost():
    x = torch.randn(4096, 1536, dtype=torch.bfloat16).npu()
    w = torch.randn(1536, 4096, dtype=torch.bfloat16).npu()

    # baseline: 每次临时转置
    t1 = time.time()
    for _ in range(100):
        y = torch.matmul(x, w.T)
    torch.npu.synchronize()
    t2 = time.time()
    print("临时转置耗时:", t2 - t1, "s")

    # 优化后：预转置一次
    w_opt = w.T.contiguous()
    t3 = time.time()
    for _ in range(100):
        y = torch.matmul(x, w_opt)
    torch.npu.synchronize()
    t4 = time.time()
    print("提前转置耗时:", t4 - t3, "s")

test_transpose_cost()

实测结果直观展示：提前转置能减少 15%~25% 的整体矩阵乘耗时。

---

7. 代码：训练性能统计脚本

最后可以附带一段性能采集逻辑，用于评估整体吞吐：

import time

def benchmark_training(model, dataloader, steps=100):
    start = time.time()
    for i, batch in enumerate(dataloader):
        if i >= steps:
            break
        loss = model(batch)
        loss.backward()
    torch.npu.synchronize()
    end = time.time()
    print(f"Avg step time: {(end - start) / steps * 1000:.2f} ms")

# 比较两种方案
print("=== Baseline (ND) ===")
benchmark_training(model_nd, dataloader)

print("=== With sliceNZ + Pre-Transpose ===")
benchmark_training(model_nz, dataloader)

配合 tokens/s 统计，就能量化最终性能收益。

---

七、总结与启示

整个 GMM NZ 训练使能过程，从框架底层到算子适配，经历了多次性能权衡与调试。 最终的经验可总结为：

• 一次搬运，双重优化：sliceNZ 的核心价值在于合并 slice 与格式转换；
• 格式识别是关键：PTA 层需正确识别 NZ 格式，才能真正走高性能路径；
• 冗余操作要前移处理：提前转置可显著减少训练时的算子级开销；
• 验证手段要量化：profiling 数据是判断优化是否有效的唯一依据。

在推理端验证的性能思路，迁移到训练端有时候并不是简单的复用。 但是通过算子融合、前后向一体化设计与格式识别优化， GMM NZ 的潜力在训练端才被真正激活。

未来，随着 PTA 主线对 NZ 支持的持续完善， 这套方案也将更容易被开发者直接复用在更大规模的模型训练中。

注明：昇腾PAE案例库对本文写作亦有帮助。