Dijkstra算法

最新推荐文章于 2022-10-28 21:06:33 发布

原创最新推荐文章于 2022-10-28 21:06:33 发布 · 127 阅读

0 ·

CC 4.0 BY-SA版权

那些年程序员学过的算法专栏收录该内容

38 篇文章

订阅专栏

本文深入解析了Dijkstra算法，一种用于解决带权图中单源最短路径问题的经典算法。通过详细的代码示例，展示了如何从一个源点出发，计算到图中所有其他顶点的最短路径。

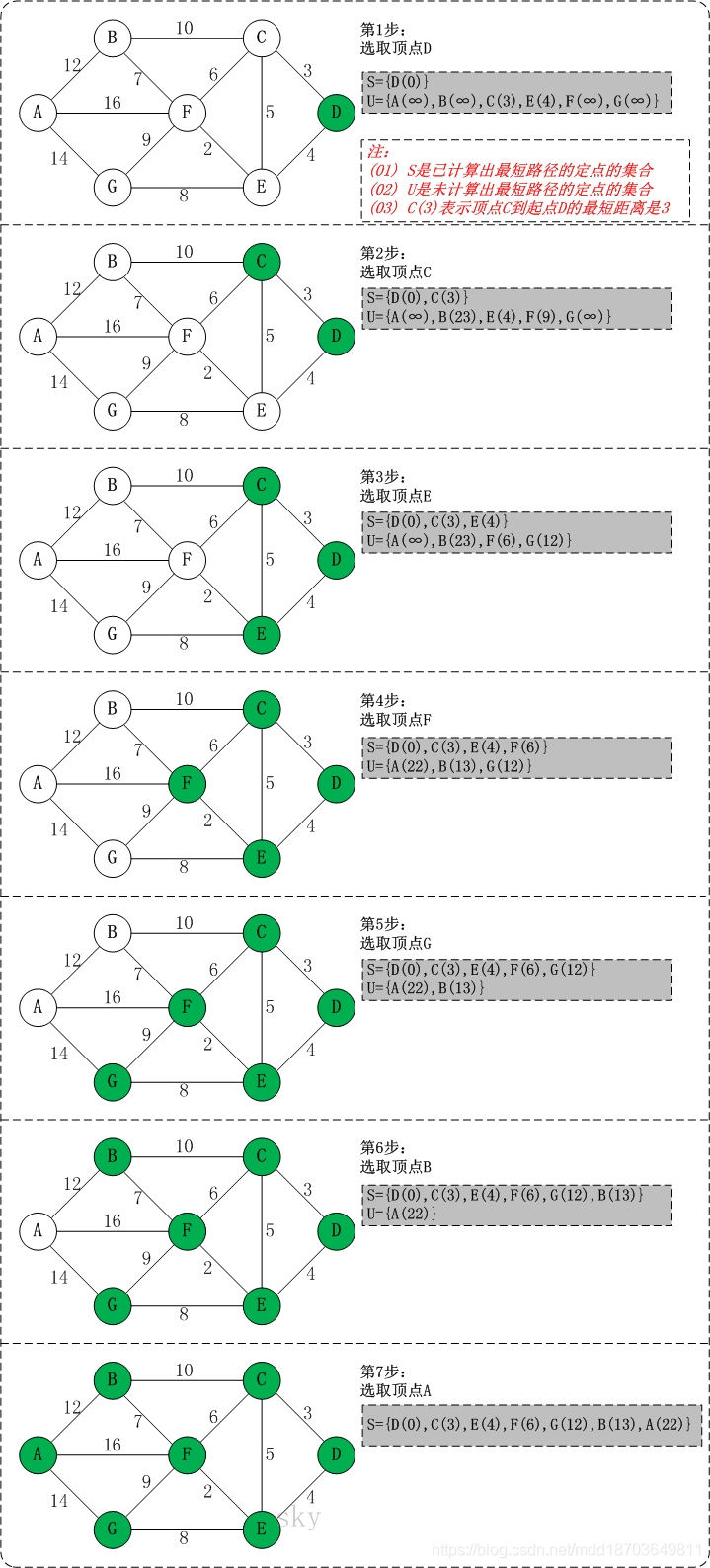
从某个源点到其余各顶点的最短路径
在这里插入图片描述

package com.routeSearch.route;

public class Dijkstra {
    private int[] distance;
    private int[] route;
    private static int Max = 999;

    /**
     * 求顶点begin到顶点i的最小距离。
     * @param begin 开始顶点
     * @param costs 图的邻接矩阵
     */
    public void dijkstra(int begin,int[][] costs){
        if( costs == null || (begin<0 && begin>costs.length) ){
            throw new RuntimeException("传入的参数不合法...");
        }
        boolean[] flag = new boolean[costs.length];
        distance = new int[costs.length];
        route = new int[costs.length];
        //初始化
        for(int i=0;i<costs.length;i++){
            flag[i] = false;
            route[i] = 0;
            distance[i] = costs[begin][i];
        }
        //初始化开始顶点
        flag[begin] = true;
        distance[begin] = 0;

        int k = 0;
        for(int i=0;i<costs.length;i++){
            // 寻找当前最小的路径；
            // 即，在未获取最短路径的顶点中，找到离vs最近的顶点(k)。
            int min = Max;
            for(int j=0;j<costs.length;j++){
                if(flag[j] == false && distance[j] < min){
                    min = distance[j];
                    k = j;
                }
            }
            //标记"顶点k"为已经获取到最短路径
            flag[k] = true;
            // 修正当前最短路径和前驱顶点
            // 即，当已经"顶点k的最短路径"之后，更新"未获取最短路径的顶点的最短路径和前驱顶点"。
            for(int j=0;j<costs.length;j++){
                int temp = (costs[k][j] == Max) ? Max : (min+costs[k][j]);
                if(flag[j] == false && temp<distance[j]){
                    distance[j] = temp;
                    route[j] = k;
                }
            }
        }
    }
    /**
     *
     * @return 最短距离
     */
    public int[] getDistance() {
        return distance;
    }
    /**
     *
     * @return 顶点start"到"顶点i"的最短路径所经历的全部顶点中，位于"顶点i"之前的那个顶点。
     */
    public int[] getRoute() {
        return route;
    }
}